洛谷 P2341 【受欢迎的牛】

• 题库：洛谷
• 题号：2341
• 题目：受欢迎的牛
• link：https://www.luogu.org/problemnew/show/P2341

---

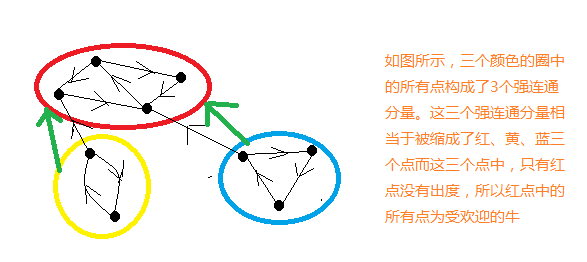
思路：因为奶牛的爱慕关系具有传递性，所以每个环(强连通分量)里的奶牛是互相喜欢的。那么我们可以用到Tarjan算法把每个强连通分量找出，并缩点，把每个强连通分量都缩成一个点(当前缩点里的奶牛都是互相喜欢的)。这样一来，这个图就变成了一个DAG(有向无环图)。然后我们只需要统计每个缩点的出度就好了，如果一个点有出度&&我们知道这个图是一个DAG，所以这个强连通分量(这个缩点)里的奶牛就不可能被这个缩点所连出去的缩点里的奶牛所喜欢(这是无环图——DAG)。综上所述，我们只需要统计一下有多少个没有出度的强连通分量就好了，但有多个没有出度的强连通分量也不行，因为这样就会有两多群群奶牛不喜欢别的奶牛，使得奶牛们无法收到其他奶牛(这多群奶牛)的喜欢，这样就不行了 。

画一张图形象一下：

code ：

 #include <bits/stdc++.h>
 #define INF 0x3f3f3f3f
 using namespace std;
 const int MAX = 5e4 + ;
 stack < int > pru;
 int n, m, low[MAX], dfn[MAX], head[MAX], vis[MAX], col[MAX], sum[MAX], color, num, z, out[MAX], ans, cnt;
 struct node
 {
     int next, to;
 }stu[MAX];
 inline void add(int x, int y)
 {
     stu[++num].next = head[x];;
     stu[num].to = y;
     head[x] = num;
     return;
 }
 inline void tarjan(int u)//Tarjan算法模板，这里用于缩点
 {
     low[u] = dfn[u] = ++z;
     vis[u] = ;
     pru.push(u);
     for(register int i = head[u]; i; i = stu[i].next)
     {
         int k = stu[i].to;
         if(!vis[k])
         {
             tarjan(k);
             low[u] = min(low[u], low[k]);
         }
         else if(!col[k])
         {
             low[u] = min(low[u], dfn[k]);
         }
     }
     if(low[u] == dfn[u])
     {
         col[u] = ++color;
         ++sum[color];//当前强连通分量里的奶牛的个数++
         while(pru.top() != u)
         {
             col[pru.top()] = color;
             ++sum[color];//当前强连通分量里的奶牛的个数++
             pru.pop();
         }
         pru.pop();
     }
     return;
 }
 signed main()
 {
     scanf("%d %d", &n, &m);
     for(register int i = , x, y; i <= m; ++i)
     {
         scanf("%d %d", &x, &y);
         add(y, x);//建反向边，把统计出度变为统计入度，更加方便一些
     }
     for(register int i = ; i <= n; ++i)
     {
         if(!vis[i])
         {
             tarjan(i);
         }
     }
     for(register int u = ; u <= n; ++u)//循环每个结点的出度(这里是入度，因为建的是反向边)
     {
         for(register int i = head[u]; i; i = stu[i].next)
         {
             int k = stu[i].to;//因为建的是反向边，所以i其实是k的出度
             if(col[k] != col[u])//颜色不相同就代表不在一个强连通分量里
             {
                 ++out[col[k]];//所以k的颜色(及包含k的那个强连通分量)就不能选了(这里标记为出度++)，至于为什么思路里有讲
             }
         }
     }
     for(register int i = ; i <= color; ++i)//枚举每种颜色(每个强连通分量)
     {
         if(!out[i])//要是没有出度(及当前强连通分量中没有奶牛喜欢别的奶牛)
         {
             ++cnt;//记录有几个强连通分量的缩点没有出度
             ans = sum[i];//注意，这里是sum[i]，因为i点只是当前强连通分量的缩点，真正被所有奶牛都喜欢的奶牛个数其实是这个强连通分量的大小(及当前强连通分量中奶牛的个数)
         }
     }
     if(cnt == )//必须只有一个强连通分量没有出度，如果有多个也不行，因为这样那两个强连通分量里的奶牛都是不互相喜欢的
     {
         printf("%d", ans);
     }
     else
     {
         printf("");//没有奶牛被所有奶牛喜欢
     }
     return ;
 }