数理统计（一）——用Python进行方差分析

　　iwehdio的博客园：https://www.cnblogs.com/iwehdio/

　　方差分析可以用来推断一个或多个因素在其状态变化时，其因素水平或交互作用是否会对实验指标产生显著影响。主要分为单因素方差分析、多因素无重复方差分析和多因素重复方差分析。
　　做数理统计课后题，发现方差分析计算比较麻烦，想用Python掉包实现。但是发现大多教程对参数的讲解不是很清楚，在此做记录。
　　主要用到的库是pandas和statsmodels。简要流程是，先用pandas库的DataFrame数据结构来构造输入数据格式。然后用statsmodels库中的ols函数得到最小二乘线性回归模型。最后用statsmodels库中的anova_lm函数进行方差分析。

import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm

​ 　　首先，是输入的数据格式。使用pandas的DataFrame，每一行为一次试验的因素水平和试验结果。以下图中的题目为例。

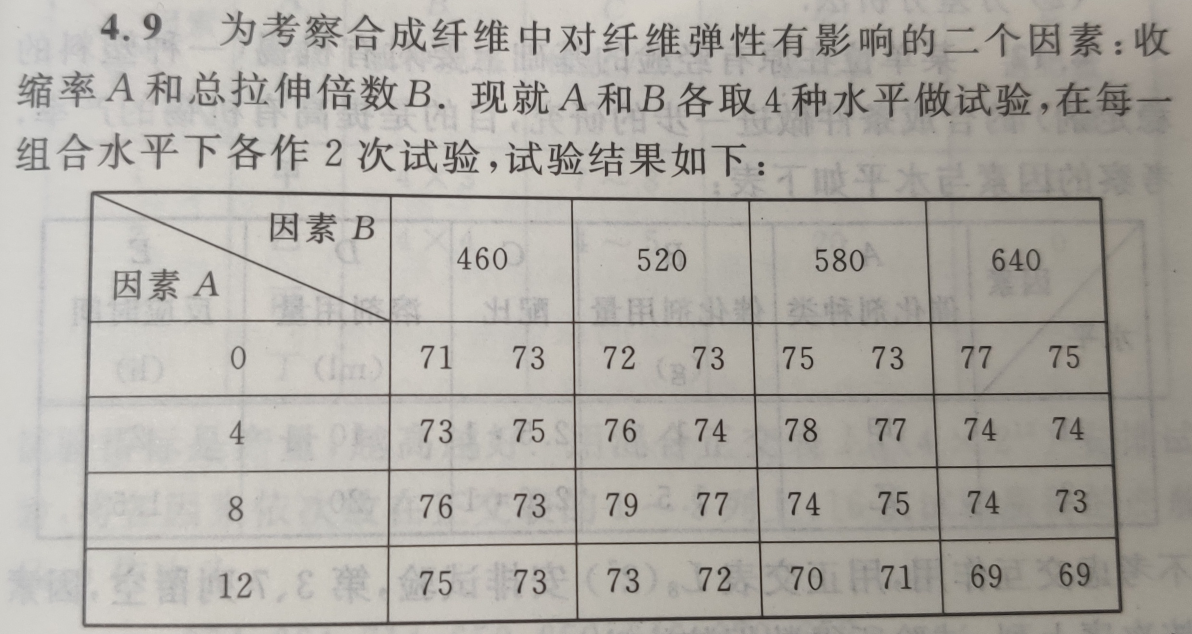
　　则对于因素A和因素B即结果R可表示为如下的DataFrame：

data = pd.DataFrame([[1, 1, 32],
                     [1, 2, 35],
                     [1, 3, 35.5],
                     [1, 4, 38.5],
                     [2, 1, 33.5],
                     [2, 2, 36.5],
                     [2, 3, 38],
                     [2, 4, 39.5],
                     [3, 1, 36],
                     [3, 2, 37.5],
                     [3, 3, 39.5],
                     [3, 4, 43]],
                    columns=['A', 'B', 'value'])

​　　 第一列为因素A的水平，第二列为因素B的水平，第三列为试验结果。在方差分析中，只关心每次试验中因素水平是否相同，所以我们可以把较为复杂的因素水平抽象为标签值 1,2,3。　　

​ 　　然后，输入ols函数。主要用到该函数的两个参数，formula和data。
　　formula指定了：
　　　　　　　　①试验结果是哪一列。
　　　　　　　　②需要计算的是哪几个因素水平对结果的影响。
　　　　　　　　③是否计算交互作用。
​
　　formula的类型为字符串，输入格式为如果试验结果的列名为‘value’，需要计算的因素的列名为‘A’和‘B’，则示例如下。

# 因素A的水平对结果的影响
'value ~ C(A)'

# 因素A和因素B的水平对结果的影响
'value ~ C(A) + C(B)'

# 因素A和因素B以及A和B的交互作用的水平对结果的影响
'value ~ C(A) + C(B) + C(A)*C(B)'

# 多因素无重复试验，不计算交互作用的影响
model = ols('value~C(A) + C(B)', data=data[['A', 'B', 'value']]).fit()
anovat = anova_lm(model)
print(anovat)

　　data为之前生成的DataFrame中选出的进行分析所需要的列，实际上ols是通过DataFrame的列名来获得试验结果和因素水平的数据的。
　　最后用ols函数进行最小二乘线性拟合，用anova_lm函数进行方差分析并输出结果。之前题目输出的结果为：

　　Residual表示误差，df表示自由度，sum_sq表示离差平方和，mean_sq表示均方离差，F表示F值，PR(>F)表示F值所对应的显著水平α。
　　进行单因素多方差分析，将formula中的C(B)去掉即可。如果是对于有重复的多因素方差分析，示例如下：

　　结果为：　

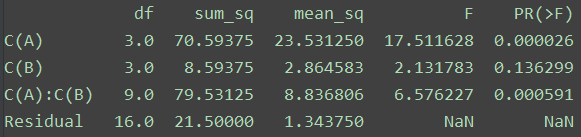
参考：施雨 《应用数理统计(西安交通大学)》 课后习题 4.1,4.3,4.5,4.6,4.9
　　　python做单因素方差分析：https://www.cnblogs.com/jin-liang/p/9852321.html
　　　Python数据科学：方差分析：https://blog.csdn.net/Kaitiren/article/details/85066793

iwehdio的博客园：https://www.cnblogs.com/iwehdio/