线性回归 python 代码实现
本代码参考自:https://github.com/lawlite19/MachineLearning_Python#%E4%B8%80%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92
首先,线性回归公式:y = X*W +b 其中X是m行n列的数据集,m代表样本的个数,n代表每个样本的数据维度。则W是n行1列的数据,b是m行1列的数据,y也是。
损失函数采用MSE,采用梯度下降法进行训练
1 .加载数据集并进行读取
def load_csvdata(filename,split,dataType): #加载数据集
return np.loadtxt(filename,delimiter = split,dtype = dataType) def read_data(): #读取数据集
data = load_csvdata("data.txt",split=",",dataType=np.float64)
print(data.shape)
X = data[:,0:-1] #取data的前两列
y = data[:,-1] #取data的最后一列作为标签
return X,y
2 . 对数据进行标准化
def feature_normalization(X):
X_norm = np.array(X)
mu = np.zeros((1,X.shape[1]))
std = np.zeros((1,X.shape[1]))
mu = np.mean(X_norm,0)
std = np.std(X_norm,0)
for i in range(X.shape[1]):
X_norm[:,i] = (X_norm[:,i] - mu[i]) / std[i]
return X_norm,mu,std
3. 损失值的计算
def loss(X,y,w):
m = len(y)
J = 0
J = (np.transpose(X*w - y))*(X*w - y) / (2*m)
print(J)
return J
4. 梯度下降算法的python实现
def gradientDescent(X,y,w,lr,num_iters):
m = len(y) #获取数据集长度
n = len(w) #获取每个输入数据的维度
temp = np.matrix(np.zeros((n,num_iters)))
J_history = np.zeros((num_iters,1))
for i in range(num_iters): #进行迭代
h = np.dot(X,w) #线性回归的矢量表达式
temp[:,i] = w - ((lr/m)*(np.dot(np.transpose(X),h-y))) #梯度的计算
w = temp[:,i]
J_history[i] = loss(X,y,w)
return w,J_history
5. 绘制损失值随迭代次数变化的曲线图
def plotLoss(J_history,num_iters):
x = np.arange(1,num_iters+1)
plt.plot(x,J_history)
plt.xlabel("num_iters")
plt.ylabel("loss")
plt.title("Loss value changes with the number of iterations")
plt.show()
6. 主函数
if __name__ == "__main__":
X,y = read_data()
X,mu,sigma = feature_normalization(X)
m = len(y) #样本的总个数
X = np.hstack((np.ones((m,1)),X)) #在x上加上1列是为了计算偏移b X=[x0,x1,x2,......xm] 其中x0=1 y = x*w
y = y.reshape((-1,1))
lr = 0.01
num_iters = 400
w = np.random.normal(scale=0.01, size=((X.shape[1],1)))
theta,J_history = gradientDescent(X,y,w,lr,num_iters)
plotLoss(J_history,num_iters)
7.结果
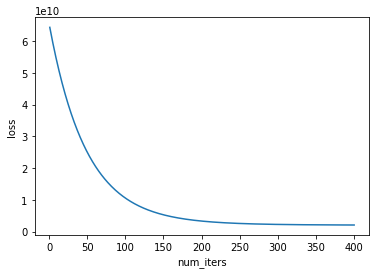
线性回归 python 代码实现的更多相关文章
- 线性回归——Python代码实现
import numpy as np def computer_error_for_give_point(w, b, points): # 计算出 观测值与计算值 之间的误差, 并累加,最后返回 平均 ...
- 梯度下降法的python代码实现(多元线性回归)
梯度下降法的python代码实现(多元线性回归最小化损失函数) 1.梯度下降法主要用来最小化损失函数,是一种比较常用的最优化方法,其具体包含了以下两种不同的方式:批量梯度下降法(沿着梯度变化最快的方向 ...
- 【机器学习】线性回归python实现
线性回归原理介绍 线性回归python实现 线性回归sklearn实现 这里使用python实现线性回归,没有使用sklearn等机器学习框架,目的是帮助理解算法的原理. 写了三个例子,分别是单变量的 ...
- 机器学习/逻辑回归(logistic regression)/--附python代码
个人分类: 机器学习 本文为吴恩达<机器学习>课程的读书笔记,并用python实现. 前一篇讲了线性回归,这一篇讲逻辑回归,有了上一篇的基础,这一篇的内容会显得比较简单. 逻辑回归(log ...
- 一元回归1_基础(python代码实现)
python机器学习-乳腺癌细胞挖掘(博主亲自录制视频) https://study.163.com/course/introduction.htm?courseId=1005269003&u ...
- 李宏毅机器学习课程笔记-2.5线性回归Python实战
本文为作者学习李宏毅机器学习课程时参照样例完成homework1的记录. 任务描述(Task Description) 现在有某地空气质量的观测数据,请使用线性回归拟合数据,预测PM2.5. 数据集描 ...
- 可爱的豆子——使用Beans思想让Python代码更易维护
title: 可爱的豆子--使用Beans思想让Python代码更易维护 toc: false comments: true date: 2016-06-19 21:43:33 tags: [Pyth ...
- if __name__== "__main__" 的意思(作用)python代码复用
if __name__== "__main__" 的意思(作用)python代码复用 转自:大步's Blog http://www.dabu.info/if-__-name__ ...
- Python 代码风格
1 原则 在开始讨论Python社区所采用的具体标准或是由其他人推荐的建议之前,考虑一些总体原则非常重要. 请记住可读性标准的目标是提升可读性.这些规则存在的目的就是为了帮助人读写代码,而不是相反. ...
随机推荐
- [Leetcode][动态规划] 零钱兑换
一.题目描述 给定不同面额的硬币 coins 和一个总金额 amount.编写一个函数来计算可以凑成总金额所需的最少的硬币个数.如果没有任何一种硬币组合能组成总金额,返回 -1. 示例 1: 输入: ...
- MySQL中常用到的关于时间的SQL
-- 今天 SELECT DATE_FORMAT(NOW(),'%Y-%m-%d 00:00:00') AS dayStart;SELECT DATE_FORMAT(NOW(),'%Y-%m-%d 2 ...
- supervisor模块学习使用
supervisor组件 supervisord supervisord是supervisor的服务端程序. 启动supervisor程序自身,启动supervisor管理的子进程,响应来自clien ...
- 用call或bind实现bind()
一.bind方法 让我们看一下MDN上对bind方法的解释 bind()方法创建一个新的函数,在bind()被调用时,这个新函数的this被bind的第一个参数指定,其余的参数将作为新函数的参数供调用 ...
- 自己动手实现智能家居之树莓派GPIO简介(Python版)
[前言] 一个热爱技术的人一定向往有一个科技感十足的环境吧,那何不亲自实践一下属于技术人的座右铭:“技术改变世界”. 就让我们一步步动手搭建一个属于自己的“智能家居平台”吧(不要对这个名词抬杠啦,技术 ...
- 基于操作系统原理的Linux 的基本操作和常用命令的使用
一.实验目的 1.学会不同Linux用户登录的方法. 2.掌握常用Linux命令的使用方法. 3.了解Linux命令中参数选项的用法和作用. 二.实验内容 1. 文件操作命令 (1) 查看文件与目录 ...
- Linux版本号的数值含义
Linux内核版本有两种:稳定版和开发版 ,Linux内核版本号由3组数字组成:第一个组数字.第二组数字.第三组数字.第一个组数字:目前发布的内核主版本.第二个组数字:偶数表示稳定版本:奇数表示开发中 ...
- 在Debian上用FVWM做自己的桌面
用FVWM做自己的桌面 Table of Contents 1. 前言 2. 学习步骤 3. 准备 3.1. 软件包 3.2. 字体 3.3. 图片 3.4. 参考资料 4. 环境 5. 布局 6. ...
- Spring Boot (七): Mybatis极简配置
Spring Boot (七): Mybatis极简配置 1. 前言 ORM 框架的目的是简化编程中的数据库操作,经过这么多年的发展,基本上活到现在的就剩下两家了,一个是宣称可以不用写 SQL 的 H ...
- UML图标含义及记忆方法
记忆技巧: 箭头的一方为被动方(被调用者): 箭头的端点为主动方(调用者). 箭头为封闭三角形时,表示类间关系 箭头为半封闭尖括号时,表示类内关系.其中,虚线表示参数强制依赖关系,实线表示属性关系.一 ...
