数据结构（四十七）归并排序（O(nlogn)）

　　一、归并排序的定义

　　归并排序（Merging Sort）就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到【n/2】个长度为2或1的有序子序列；再两两归并，...，如此反复，直到得到一个长度为n的有序序列为止，这种排序方法称为2路归并排序。

　　

　　二、归并排序算法的实现

    private static void merge(int[] a, int[] swap, int k) {
        int n = a.length;
        int m = 0, i, j;

        int end1, start2, end2;
        int start1 = 0;                                                    // 第一个有序子数组下界

        while (start1 + k <= n - 1) {
            start2 = start1 + k;                                        // 第二个有序子数组下界
            end1 = start2 - 1;                                            // 第一个有序子数组上界
            end2 = (start2 + k - 1 <= n - 1)? start2 + k - 1 : n - 1;    // 第二个有序子数组上界

            for (i = start1, j = start2; i <= end1 && j <= end2; m++) { // 将k-1个数从小到大排列并写入swap数组
                if (a[i] <= a[j]) {
                    swap[m] = a[i];
                    i++;
                } else {
                    swap[m] = a[j];
                    j++;
                }
            }

            while (i <= end1) {        // 如果i越界就把k个数中值最大的放在swap数组的区间数组最后一位
                swap[m] = a[i];
                m++;
                i++;
            }

            while (j <= end2) {        // 如果j越界就把k个数中值最大的放在swap数组的区间数组最后一位
                swap[m] = a[j];
                m++;
                j++;
            }

            start1 = end2 + 1;        // 从下一个k区间的第一个数开始
        }

        for (i = start1; i < n; i++, m++) {    // 将原始数组中只够一组的数据元素顺序存放到数组swap中
            swap[m] = a[i];
        }
    }

    public static void mergeSort(int[] a) {
        int k = 1;                                    // 归并长度从1开始
        int[] swap = new int[a.length];

        while (k < a.length) {
            merge(a, swap, k);

            for (int i = 0; i < a.length; i++) {    // 将调整后的元素重新放回原始数组中
                a[i] = swap[i];
            }
            System.out.print("k值为" + k + "时: ");
            print(a);

            k = 2 * k;                                // 归并长度为原来的二倍
        }
    }

　　结合代码分析代码执行过程

int[] array1 = {50,10,90,30,70,40,80,60,20};

k=1时，swap={0,0,0,0,0,0,0,0,0}，执行merge方法，
　　m=0,start1=0且0+1<=8进入while,start2=1,end1=0,end2=1，
　　　　进入for循环,i=0,j=1,a0=50,a1=10,swap[0]=10,j=2,m=1,j<=end2不成立，跳出for，进入i的while，swap[1]=50,m=2,i=1,start1=2,也就是交换50和10并放入swap数组的前两位
　　m=2,start1=2且2+1<=8进入while,start2=3,end1=2,end2=3,
　　　　进入for循环,i=2,j=3,a2=90,a3=30,swap[2]=30,j=4,m=3,j<=end2不成立，跳出for，进入i的while，swap[3]=90,m=4,i=2,start1=4,也就是交换90和30并放入swap数组的前两位
　　同理，交换70和40，交换80和60，然后a[]=swap[]={10 50 30 90 40 70 60 80 20}

k=2时，swap={10,50,30,90,40,70,60,80,20}，执行merge方法，
　　m=0,start1=0且0+2<=8进入while,start2=2,end1=1,end2=3，
　　　　进入for循环,i=0,j=2,a0=10,a2=30,swap[0]=10,i=1,m=1,
　　　　进入for循环,i=1,j=2,a1=50,a2=30,swap[1]=30,j=3,m=2,
　　　　进入for循环,i=1,j=3,a1=50,a3=90,swap[2]=50,i=2,m=3
　　　　i=2<=end1不成立，跳出for，进入j的while，j=3<=3.swap[3]=a3=90,也就是将数组的前四位按顺序排列即将10 50 30 90变成10 30 50 90
　　　　同理，将40 70 60 80变成40 60 70 80

其他同理：
k值为4时: 10 30 40 50 60 70 80 90  20 
k值为8时: 10 20 30 40 50 60 70 80 90 

　　过程用图片表示为：

　　

　　

　　

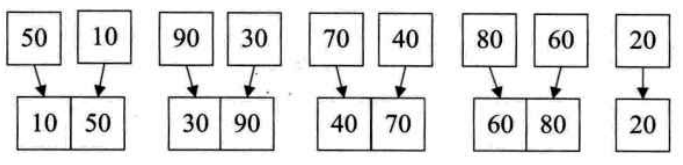
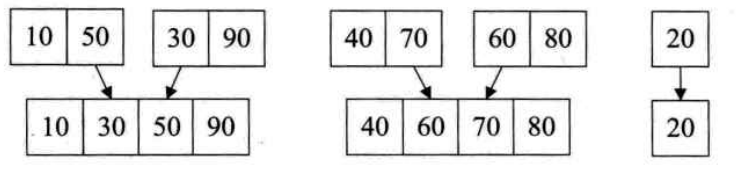
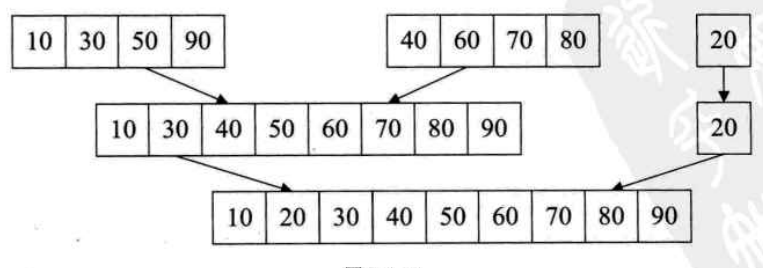
　　测试代码和输出为：

    public static void main(String[] args) {

        int[] array1 = {50,10,90,30,70,40,80,60,20};
        System.out.print("归并排序前: ");
        print(array1);
        mergeSort(array1);
        System.out.print("归并排序后: ");
        print(array1);

    }

归并排序前: 50 10 90 30 70 40 80 60 20
k值为1时: 10 50 30 90 40 70 60 80 20
k值为2时: 10 30 50 90 40 60 70 80 20
k值为4时: 10 30 40 50 60 70 80 90 20
k值为8时: 10 20 30 40 50 60 70 80 90
归并排序后: 10 20 30 40 50 60 70 80 90 

　　三、归并排序算法的性能分析

　　（1）时间复杂度

　　示例中有9个数时，k的值分别为1,2,4,8，即需要进行4次归并，

　　则n个元素进行归并排序算法时需要进行【logn】+1次归并运算，而每一次归并运算内比较的次数都为n-1，所以二路归并排序算法的时间复杂度为O(nlogn)。。

　　对于归并排序来说，最好、最坏、平均情况下的时间复杂度均为O(nlogn)。

　　（2）空间复杂度

　　由于二路归并排序时使用了n个临时内存空间存放数据元素，所以，二路归并排序算法的空间复杂度为O(n)。

　　（3）稳定性

　　由于二路归并排序算法是相邻有序子表两两归并，对于相同的两个数据元素，则能够保证原来在前边的元素排序后仍在前边。因此，二路归并排序算法是一种稳定的排序算法。

　　二路排序算法不仅时间复杂度是O(nlogn)，而且还是一种稳定的排序算法，这一点是二路归并排序算法的最大特点。