队列&广搜

搜索里有深搜，又有广搜，而广搜的基础就是队列。

队列是一种特殊的线性表，只能在一段插入，另一端输出。输出的那一端叫做队头，输入的那一端叫队尾。是一种先进先出（FIFO）的数据结构。

正经的队列：

头文件：#include <queue>

入队：q.push(要入队的数)

返回第一个元素：q.front( )

从队列中移除第一个元素：q.pop( )

查看队列中元素的个数：q.size( )

返回队列的最后一个元素：q.back( )

用数组模拟的队列：

可以定义数组q[100001](可大可小)

队头为head,队尾为tail

注意：

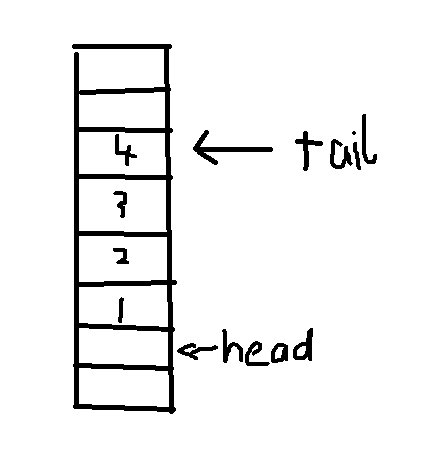
如图，head指向第一个实际元素的前一个位置，tail指向最后一个实际元素的位置

无论数组多大，总会有个界限，入队过多会溢出，而前面出队时会有空出来的位置，所以我们可以把一个数组循环使用。

代码如下：

void rudui(int x)
{tail++:
   if(tail==n+)
     tail=;
  if(tail==head)//入队要判满
   {printf("操作无效，队列已满");
    return;}
    q[tail]=x;
}

说了些基本定义，再来说说应用。

队列的应用和广搜是分不开的。

那什么是广搜？

就是一层一层的搜索，从第0层开始，每层都枚举出可能的情况，直到找到符合要求的情况为止

如图：

放个模板

这里是用数组模拟队列
int  bfs()
{ 队列初始化；
   head=;tail=;//记住tail指向最后一个实际元素！！
  do{
         head++;//head指向带扩展节点
       for(int i=;i<=max;i++)//节点如何扩展
         {
                   if(子节点符合条件)
                       {tail++;该节点入队；
                          if(与原来有重复)
                               { 删除该节点；tail--;
                               }
                           else
                                {if(找到目标)输出并退出；
                                 }
                         }
          }
      }while(head<tail);//队列不空就继续搜索
}

举个栗子：

例题1：

洛谷P1451求细胞数量

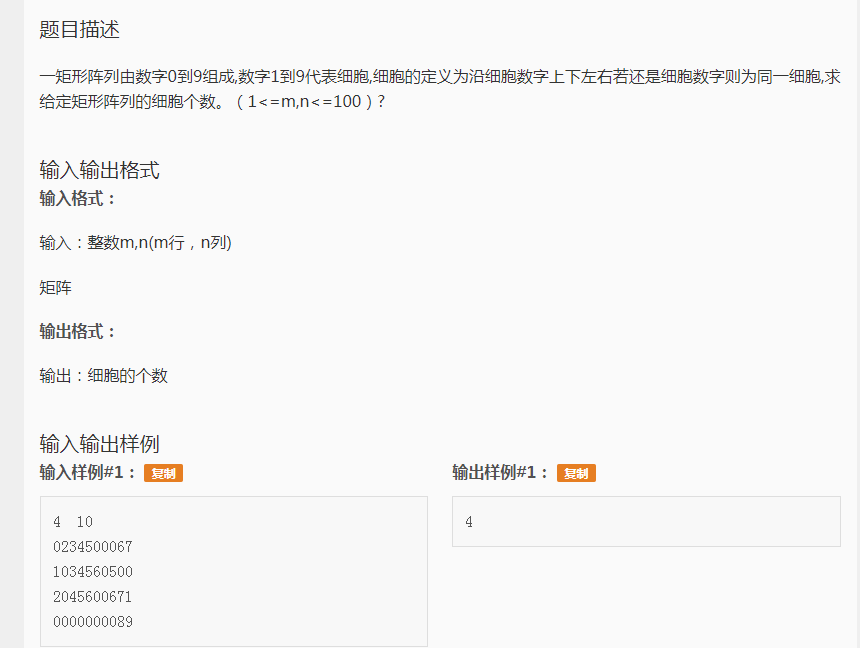
这个题就是广搜的典型例题。

在这道题中，所有非0数都可以看做是1，因为它们的值不影响判断。这样就可以用一个bool数组a[1001][1001]来表示这个矩阵

通过样例可以知道，矩阵的输入是没有空格的，所以要用字符型输入（这是个坑）

既然我们决定用bool型数组（只有0,1），而且还有前面那个坑。为了防止毒瘤的非法读入，我们先将整个a数组置为1。我们输入时判断一下，如果输入的字符是0，就把对应位置置为0。

然后就是搜索了。

先在main里找到1，再进行搜索，会省时间。

搜索时，记录下当前的i,j。从i,j的上下左右搜索，如果是1，就将这个位置的坐标放入队中，并将这个位置置为0，防止重复

入队的同时将队头出队，一直到队空为止，完成一次搜索，计数器加1.

代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
int n,m,num,dx[]={-,,,},dy[]={,,,-};//预处理出4个方向
bool a[][];
void justdoit(int p,int q)
{   a[p][q]=;
    int x,y,head,tail,i;
    int h[][];
    num++;
    h[][]=p;h[][]=q;//h[head][1]为横坐标，h[head][2]为纵坐标
    head=;tail=;
    do{
        head++;
        for(int i=;i<=;i++)
        {x=h[head][]+dx[i];y=h[head][]+dy[i];
           if((a[x][y])&&(x>=)&&(y>=)&&(x<m)&&(y<n))
           {tail++;
             h[tail][]=x;//坐标入队
             h[tail][]=y;
             a[x][y]=;
           }
        }
    }while(head<tail);
}//其实就是套模板
int main()
{char c[];
 scanf("%d %d",&m,&n);
 for(int i=;i<=m-;i++)
  {for(int j=;j<=n-;j++)
    a[i][j]=;
  }
  for(int i=;i<m;i++)
  {
    scanf("%s",c);
    for(int j=;j<n;j++)
     {if(c[j]==''){a[i][j]=;
     }
     }
  }
  for(int i=;i<m;i++)
  {for(int j=;j<n;j++)
    if(a[i][j])justdoit(i,j);
  }
  printf("%d",num);
}

例题2：

一本通之求最小步数

这个题显然没有什么数学规律可以解方程什么的，所以我们好像只能搜索了。

从a,b两点搜索到1会造成一些时间的浪费，因为（1,1）在棋盘的一角，而a和b在棋盘中间，会造成在左下角方向的浪费

如图：

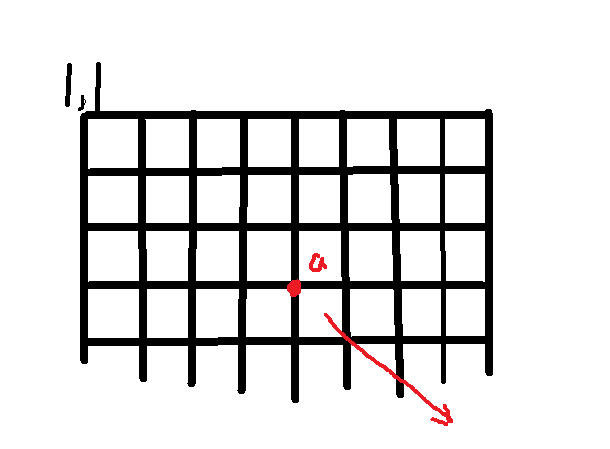
如果从a搜索到（1,1），会造成在箭头方向上的浪费，所以我们从（1,1）开始搜，搜到a停止

这里有两个点，参照对a的搜索方式，我们可以a,b一起搜。

先用p[101][101]数组将棋盘表示出来，所有的p[i][j]都初始化为-1,表示都没有到过

同时用dl[100001][4]数组来模仿队列，记录当前的所有到过点的坐标

其中dl[i][1]为横坐标，dl[i][2]为纵坐标，dl[i][3]为到达当前坐标所用最小步数

边界：点的横纵坐标大于0

一旦到达a和b,输出并结束程序

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int ax,ay,bx,by,dx[]={-,-,-,-,,,,,-,-,,},dy[]={-,,-,,-,,-,,-,,-,};
int numa,numb;
int main()
{
   scanf("%d%d%d%d",&ax,&ay,&bx,&by);
   int dl[][]={};
   int p[][];
   dl[][]=;dl[][]=;dl[][]=;//这里从（1,1）开始跳，跳到a,b两点坐标结束（？？？）
   memset(p,0xff,sizeof(p));//dl[i][3]记录跳到(dl[i][1],dl[i][2]的步数)
   p[][]=;//用p数组表示棋盘上的每个点，到过就+1，初始为-1（方便统计只到过一次的点）
   int head=,tail=;
   while(head<=tail)
   {
     for(int i=;i<=;i++)
        {int x=dl[head][]+dx[i],y=dl[head][]+dy[i];//12个方向
             if(x>&&y>)//若从(1,1)开始跳，则不能超出棋盘
             {
               if(p[x][y]==-)//之前没有到过这个点
               {p[x][y]=dl[head][]+;//到达点(x,y)所需要的步数p为跳到上一个(x,y)的步数再加一
                   tail++;
                   getchar();
                dl[tail][]=x;//记录坐标
             dl[tail][]=y;
             dl[tail][]=p[x][y];//记录跳到（x,y)的步数
            }
                if(p[ax][ay]>&&p[bx][by]>)//肯定不可能0步就跳到
                {printf("%d\n%d\n",p[ax][ay],p[bx][by]);
                 return ;
             }
            }
     }     head++;
   }
}