s - t 平面图最大流（附例题 bzoj 1001）

以下均移自周冬的《两极相通-浅析最大最小定理在信息学竞赛中的应用》

平面图性质

1、（欧拉公式）如果一个连通的平面图有n个点，m条边和f个面，那么f=m-n+2

2、每个平面图G都有一个与其对偶的平面图G* G*中的每个点对应G中的一个面

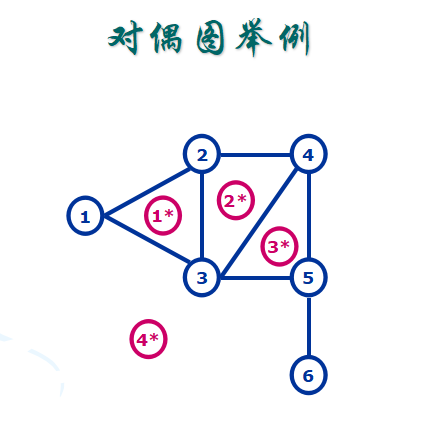
G*中的每个点对应G中的一个面

对于G中的每条边e

e属于两个面f1、f2，加入边(f1*， f2*)

e只属于一个面f，加入回边(f*， f*)

平面图G与其对偶图G*之间存在怎样的关系呢？

G的面数等于G*的点数，G*的点数等于G的面数，

G与G*边数相同 G*中的环对应G中的割一一对应

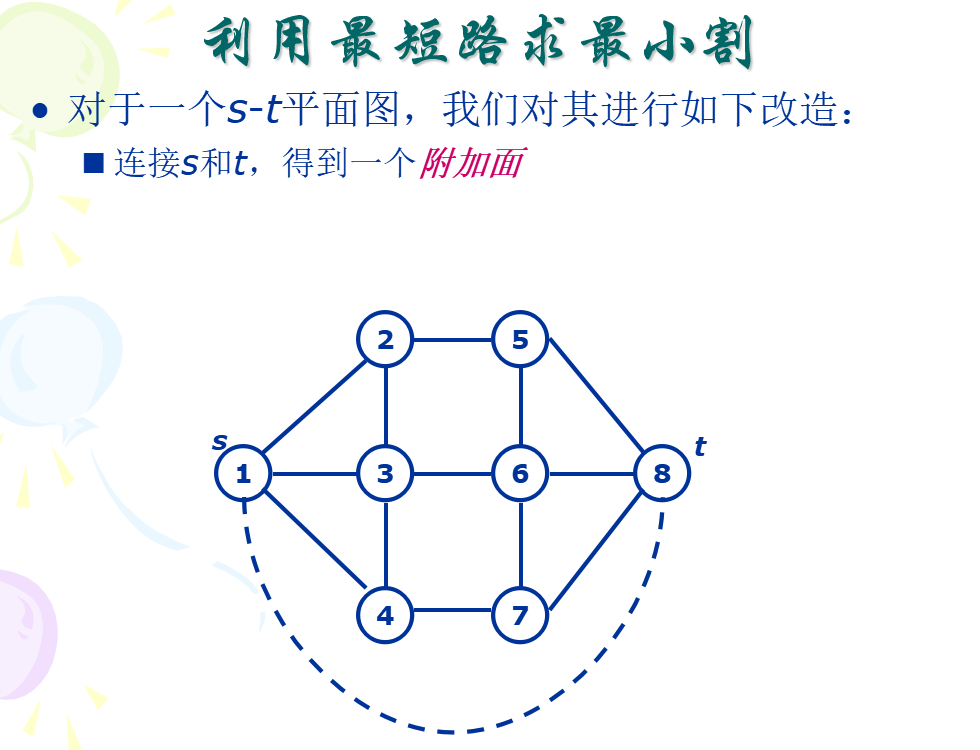
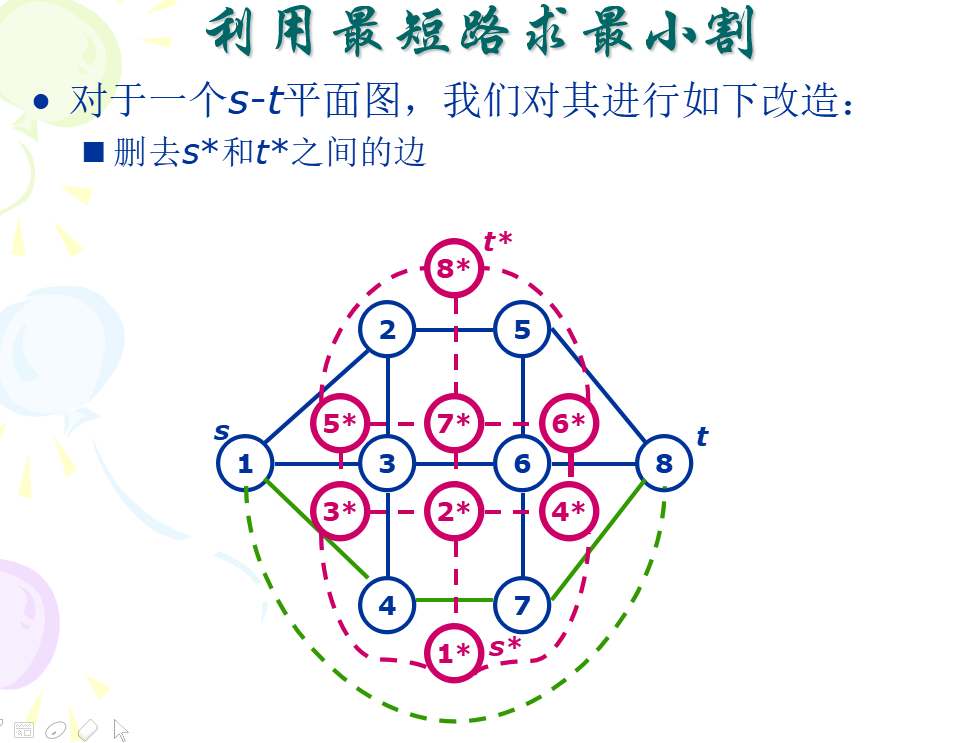
例题：BZOJ 1001

1001: [BeiJing2006]狼抓兔子

Time Limit: 15 Sec Memory Limit: 162 MB
Submit: 29380 Solved: 7697
[Submit][Status][Discuss]

Description

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，

而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路

1:(x,y)<==>(x+1,y)

2:(x,y)<==>(x,y+1)

3:(x,y)<==>(x+1,y+1)

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，

开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击

这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，

才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的

狼的数量要最小。因为狼还要去找喜羊羊麻烦.

Input

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值.

第二部分共N-1行，每行M个数，表示纵向道路的权值.

第三部分共N-1行，每行M-1个数，表示斜向道路的权值.

输入文件保证不超过10M

Output

输出一个整数，表示参与伏击的狼的最小数量.

Sample Input

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

Sample Output

解析：

　　根据上文建图

偌。。这就是建出来的图然后跑一遍spfa就好啦

对啦对啦。。。n == 1 和 m == 1 的时候要单独考虑

#include <iostream>

#include <cstdio>

#include <sstream>

#include <cstring>

#include <map>

#include <cctype>

#include <set>

#include <vector>

#include <stack>

#include <queue>

#include <algorithm>

#include <cmath>

#include <bitset>

#define rap(i, a, n) for(int i=a; i<=n; i++)

#define rep(i, a, n) for(int i=a; i<n; i++)

#define lap(i, a, n) for(int i=n; i>=a; i--)

#define lep(i, a, n) for(int i=n; i>a; i--)

#define rd(a) scanf("%d", &a)

#define rlld(a) scanf("%lld", &a)

#define rc(a) scanf("%c", &a)

#define rs(a) scanf("%s", a)

#define pd(a) printf("%d\n", a);

#define plld(a) printf("%lld\n", a);

#define pc(a) printf("%c\n", a);

#define ps(a) printf("%s\n", a);

#define MOD 2018

#define LL long long

#define ULL unsigned long long

#define Pair pair<int, int>

#define mem(a, b) memset(a, b, sizeof(a))

#define _  ios_base::sync_with_stdio(0),cin.tie(0)

//freopen("1.txt", "r", stdin);

using namespace std;

const int maxn = , INF = 0x7fffffff, LL_INF = 0x7fffffffffffffff;

int head[maxn], cnt, n, m, s, t;

int d[maxn << ], vis[maxn];

struct node

{

    int u, v, w, next;

}Node[maxn << ];

void add_(int u, int v, int w)

{

    Node[cnt].u = u;

    Node[cnt].v = v;

    Node[cnt].w = w;

    Node[cnt].next = head[u];

    head[u] = cnt++;

}

void add(int u, int v, int w)

{

    add_(u, v, w);

    add_(v, u, w);

}

bool spfa(int s)

{

    for(int i = ; i < (maxn << ); i++) d[i] = INF;

    queue<int> Q;

    mem(vis, );

    Q.push(s);

    vis[s] = ;

    d[s] = ;

    while(!Q.empty())

    {

        int u = Q.front(); Q.pop();

        vis[u] = ;

        for(int i = head[u]; i != -; i = Node[i].next)

        {

            node e = Node[i];

            if(d[e.v] > d[u] + e.w)

            {

                d[e.v] = d[u] + e.w;

                if(!vis[e.v])

                {

                    Q.push(e.v);

                    vis[e.v] = ;

                }

            }

        }

    }

    return true;

}

void init()

{

    mem(head, -);

    cnt = ;

}

int main()

{

    init();

    int u, v, w;

    cin >> n >> m;

    s = , t = n * m *  + ;

    if(n == ){

        int minn = INF;

        for(int i = ; i < m; i++){

            rd(w);

            minn = min(minn, w);

        }

        pd(minn);

        return ;

    }

    if(m == ){

        int minn = INF;

        for(int i = ; i < n - ; i++){

            rd(w);

            minn = min(minn, w);

        }

        pd(minn);

        return ;

    }

    for(int i = ; i < n; i++)

    {

        for(int j = ; j <= m - ; j++)

        {

            cin >> w;

            if(i == )

                add(t, i * (m - ) + j, w);

            else if(i == n - )

                add((n - ) * (m - ) + (i - ) * (m - ) + j, s, w);

            else

                add(i * (m - ) + j, (n - ) * (m - ) + (i - ) * (m - ) + j, w);

        }

    }

    for(int i = ; i < n - ; i++)

    {

        for(int j = ; j <= m; j++)

        {

            cin >> w;

            if(j == )

                add(s, (n - ) * (m - ) + i * (m - ) + j, w);

            else if(j == m)

                add((i + ) * (m - ), t, w);

            else

                add(i * (m - ) + (j - ), (n - ) * (m - ) + i * (m - ) + j, w);

        }

    }

    for(int i = ; i < n - ; i++)

        for(int j = ; j <= m - ; j++)

        {

            cin >> w;

            add(i * (m - ) + j, (n - ) * (m - ) + i * (m - ) + j, w);

        }

    spfa(s);

    cout << d[t] << endl;

    return ;

}