数据结构 BM算法

　　BM算法是比KMP算法更快的字符串模式匹配算法。BM算法最好情况下的时间复杂度是O(n)，KMP算法最好情况下的时间复杂度是O(n+m)，两者最坏情况下的时间复杂度均是O(m*n)。其中，n指目标串长度，m指模式串长度。

　　KMP算法从左向右比较，通过失配时已匹配的字符信息来确定下一次匹配时模式串的起始位置。BM算法从右向左比较，运用了两种启发式规则：坏字符规则和好后缀规则，取这两种规则的跳跃距离大者作为P向右跳跃的距离。

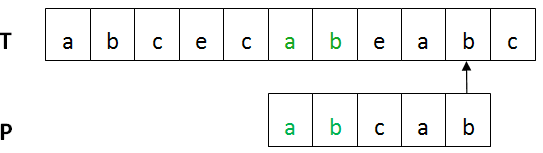
　　BM算法的基本流程：设目标串T，模式串为P。首先将T与P进行左对齐，然后进行从右向左比较 ，如下图所示：

　　

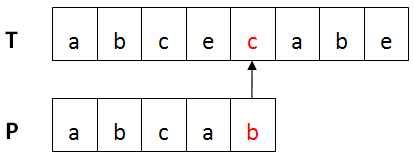
　　某趟比较不匹配时，通过坏字符规则和好后缀规则来计算模式串向右移动的距离，直到整个匹配过程的结束。

　　

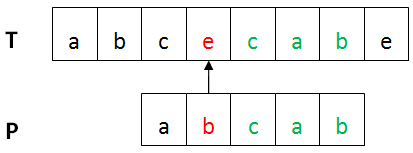
　　上图中，第一个不匹配的字符（红色部分）是坏字符，已匹配部分（绿色）是好后缀。

　　坏字符（Bad Character）规则：

　　出现某个字符x不匹配时，分如下两种情况讨论：

　　1 如果x在P中没有出现，则从x开始的m个字符不可能与P匹配成功，所以直接跳过该区域。

　　2 如果x在P中出现，则以该字符为基准右对齐。

　　设skip(x)是P右移的距离，max(x)是x在P中最右位置，用数学公式表示如下：

　　

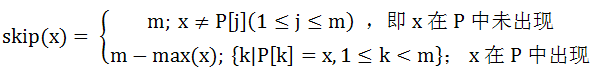
　　举例：

　　下图红色部分出现不匹配。

　　

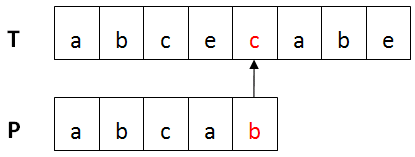
　　移动距离skip(c) = 5 - 3 = 2，则P向右移动2位。

　　移动后如下图：

　　

　　

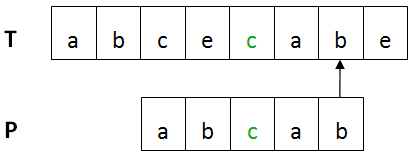
　　好后缀（Good Suffix）规则：

　　出现某个字符x不匹配时，如果已有部分字符匹配，则分如下两种情况讨论：

　　1 如果在P中位置t已匹配部分P'在P中的某位置t'也出现了，并且位置t'的前一个字符与位置t的前一个字符不相同，则将t'右移到t的位置。

　　2 如果已匹配部分P'在P中的任何位置都没有再出现，则找到与P'的后缀P''相同的在P中的最长前缀出现的位置x，将x右移到P''后缀所在的位置。

　　设Shift(j)是P右移的距离，j 是当前匹配的字符位置，s是t'与t的距离或者x与P''的距离，用数学公式表示如下：

　　

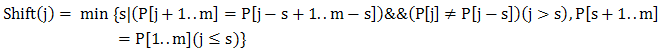
　　举例：

　　下图中，已匹配部分cab（绿色）在P中再没出现。

　　

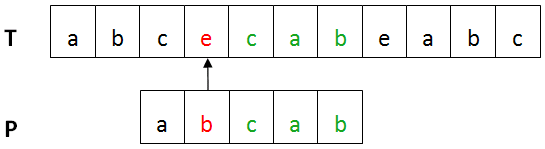
　　再看下图，已匹配部分P'中后缀T'（蓝色）与P中最长前缀P''（红色）匹配，则将P'移动到T'的位置。

　　

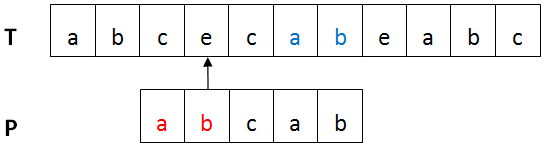
　　移动后如下图：

　　

　　取skip(x)与Shift(j)中的较大者作为跳跃的距离。

　　C语言代码

 /*
     函数：int* MakeSkip(char *, int)
     目的：根据坏字符规则做预处理，建立一张坏字符表
     参数：
         ptrn => 模式串P
         PLen => 模式串P长度
     返回：
         int* - 坏字符表
 */
 int* MakeSkip(char *ptrn, int pLen)
 {
     int i;
     //为建立坏字符表，申请256个int的空间
     /*PS:之所以要申请256个，是因为一个字符是8位，
       所以字符可能有2的8次方即256种不同情况*/
     int *skip = (int*)malloc(*sizeof(int));  

     if(skip == NULL)
     {
         fprintf(stderr, "malloc failed!");
         return ;
     }     

     //初始化坏字符表，256个单元全部初始化为pLen
     for(i = ; i < ; i++)
     {
         *(skip+i) = pLen;
     }  

     //给表中需要赋值的单元赋值，不在模式串中出现的字符就不用再赋值了
     while(pLen != )
     {
         *(skip+(unsigned char)*ptrn++) = pLen--;
     }  

     return skip;
 }  

 /*
     函数：int* MakeShift(char *, int)
     目的：根据好后缀规则做预处理，建立一张好后缀表
     参数：
         ptrn => 模式串P
         PLen => 模式串P长度
     返回：
         int* - 好后缀表
 */
 int* MakeShift(char* ptrn,int pLen)
 {
     //为好后缀表申请pLen个int的空间
     int *shift = (int*)malloc(pLen*sizeof(int));
     int *sptr = shift + pLen - ;//方便给好后缀表进行赋值的指标
     char *pptr = ptrn + pLen - ;//记录好后缀表边界位置的指标
     char c;  

     if(shift == NULL)
     {
         fprintf(stderr,"malloc failed!");
         return ;
     }  

     c = *(ptrn + pLen - );//保存模式串中最后一个字符，因为要反复用到它  

     *sptr = ;//以最后一个字符为边界时，确定移动1的距离  

     pptr--;//边界移动到倒数第二个字符（这句是我自己加上去的，因为我总觉得不加上去会有BUG，大家试试“abcdd”的情况，即末尾两位重复的情况）  

     while(sptr-- != shift)//该最外层循环完成给好后缀表中每一个单元进行赋值的工作
     {
         char *p1 = ptrn + pLen - , *p2,*p3;  

         //该do...while循环完成以当前pptr所指的字符为边界时，要移动的距离
         do{
             while(p1 >= ptrn && *p1-- != c);//该空循环，寻找与最后一个字符c匹配的字符所指向的位置  

             p2 = ptrn + pLen - ;
             p3 = p1;  

             while(p3 >= ptrn && *p3-- == *p2-- && p2 >= pptr);//该空循环，判断在边界内字符匹配到了什么位置  

         }while(p3 >= ptrn && p2 >= pptr);  

         *sptr = shift + pLen - sptr + p2 - p3;//保存好后缀表中，以pptr所在字符为边界时，要移动的位置
         /*
           PS:在这里我要声明一句，*sptr = （shift + pLen - sptr） + p2 - p3;
              大家看被我用括号括起来的部分，如果只需要计算字符串移动的距离，那么括号中的那部分是不需要的。
              因为在字符串自左向右做匹配的时候，指标是一直向左移的，这里*sptr保存的内容，实际是指标要移动
              距离，而不是字符串移动的距离。我想SNORT是出于性能上的考虑，才这么做的。
         */  

         pptr--;//边界继续向前移动
     }  

     return shift;
 }  

 /*
     函数：int* BMSearch(char *, int , char *, int, int *, int *)
     目的：判断文本串T中是否包含模式串P
     参数：
         buf => 文本串T
         blen => 文本串T长度
         ptrn => 模式串P
         PLen => 模式串P长度
         skip => 坏字符表
         shift => 好后缀表
     返回：
         int - 1表示成功（文本串包含模式串），0表示失败（文本串不包含模式串）。
 */
 int BMSearch(char *buf, int blen, char *ptrn, int plen, int *skip, int *shift)
 {
     int b_idx = plen;
     if (plen == )
         return ;
     while (b_idx <= blen)//计算字符串是否匹配到了尽头
     {
         int p_idx = plen, skip_stride, shift_stride;
         while (buf[--b_idx] == ptrn[--p_idx])//开始匹配
         {
             if (b_idx < )
                 return ;
             if (p_idx == )
             {
                 return ;
             }
         }
         skip_stride = skip[(unsigned char)buf[b_idx]];//根据坏字符规则计算跳跃的距离
         shift_stride = shift[p_idx];//根据好后缀规则计算跳跃的距离
         b_idx += (skip_stride > shift_stride) ? skip_stride : shift_stride;//取大者
     }
     return ;
 }  

　　参考资料

　　字符串模式匹配的BM算法

　　【模式匹配】更快的Boyer-Moore算法