hihoCoder 1143 : 骨牌覆盖问题·一(递推，矩阵快速幂)

【题目链接】：click here~~

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

骨牌，一种古老的玩具。今天我们要研究的是骨牌的覆盖问题：

我们有一个2xN的长条形棋盘，然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘，一共有多少种不同的覆盖方法呢？

举个例子，对于长度为1到3的棋盘，我们有下面几种覆盖方式：

提示：骨牌覆盖

提示：如何快速计算结果

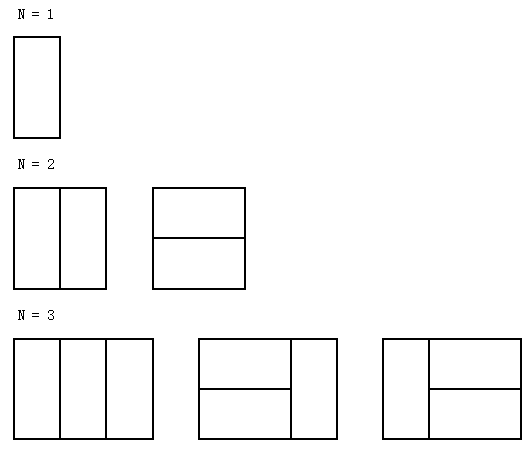
输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 19999997

样例输入

62247088

样例输出

17748018

【思路】矩阵快速幂

我们考虑在已经放置了部分骨牌(灰色)的情况下，下一步可以如何放置新的骨牌(蓝色)：

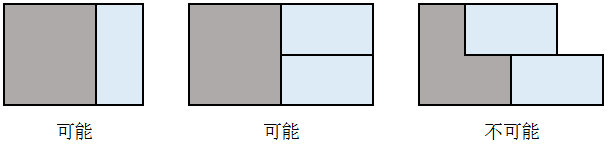
最右边的一种情况是不可能发生的，否则会始终多一个格子没有办法放置骨牌。或者说灰色部分的格子数为奇数，不可能通过1x2个骨牌放置出来。

那么通过对上面的观察，我们可以发现：

在任何一个放置方案最后，一定满足前面两种情况。而灰色的部分又正好对应了长度为N-1和N-2时的放置方案。由此，我们可以得到递推公式:

f[n] = f[n-1] + f[n-2];

这个公式是不是看上去很眼熟？没错，这正是我们的费波拉契数列。

f[0]=1,f[1]=1,f[2]=2,...

当N很小的时候，我们直接通过递推公式便可以计算。当N很大的时候，只要我们的电脑足够好，我们仍然可以直接通过递推公式来计算。

但是我们学算法的，总是这样直接枚举不是显得很Low么，所以我们要用一个好的算法来加速(装X)。

事实上，对于这种线性递推式，我们可以用矩阵乘法来求第n项。对于本题Fibonacci数列，我们希望找到一个2x2的矩阵M，使得(a, b) x M = (b, a+b)，其中(a,
b)和(b, a+b)都是1x2的矩阵。

显然，只需要取M = [0, 1; 1, 1]就可以了：

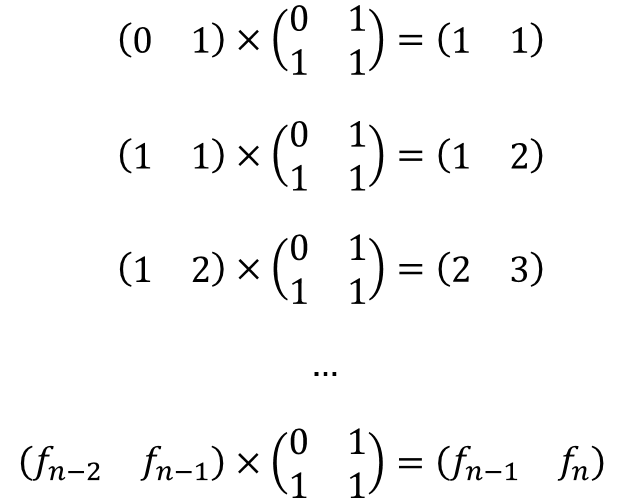
进一步得到：

那么接下来的问题是，能不能快速的计算出M^n？我们先来分析一下幂运算。由于乘法是满足结合律的，所以我们有：

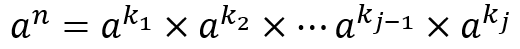
不妨将k[1]..k[j]划分的更好一点？

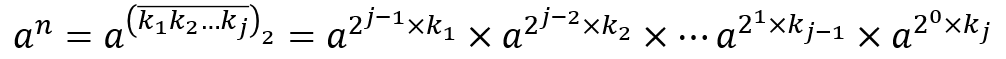
其中(k[1],k[2]...k[j])2表示将n表示成二进制数后每一位的数字。上面这个公式同时满足这样一个性质：

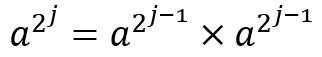
结合这两者我们可以得到一个算法：

1. 先计算出所有的{a^1, a^2, a^4 ... a^(2^j)}，因为该数列满足递推公式，时间复杂度为O(logN)

2. 将指数n二进制化，再利用公式将对应的a^j相乘计算出a^n，时间复杂度仍然为O(logN)

则总的时间复杂度为O(logN)

这种算法因为能够在很短时间内求出幂，我们称之为“快速幂”算法。

代码：

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL MOD=19999997;
LL N;
int i,j;
struct Matrlc
{
    LL mapp[2][2];
} ans,base;
Matrlc unit= {1,0,0,1};
Matrlc mult(Matrlc a,Matrlc b)    //矩阵乘法
{
    Matrlc c;
    for(int i=0; i<2; i++)
        for(int j=0; j<2; j++)
        {
            c.mapp[i][j]=0;
            for(int k=0; k<2; k++)
                c.mapp[i][j]+=(a.mapp[i][k]*b.mapp[k][j])%MOD;
            c.mapp[i][j]%=MOD;
        }
    return c;
}
LL pow(LL n)    //快速幂运算
{
    base.mapp[0][0] =base.mapp[0][1]=base.mapp[1][0]=1;
    base.mapp[1][1]=0;
    ans.mapp[0][0] = ans.mapp[1][1] = 1;// ans 初始化为单位矩阵
    ans.mapp[0][1] = ans.mapp[1][0] = 0;
    while(n)
    {
        if(n&1)   ans=mult(ans,base);
        base=mult(base,base);
        n>>=1;
    }
    return ans.mapp[0][1]%MOD;
}
int main()
{
   scanf("%lld",&N);
   printf("%lld\n",pow(N+1)%MOD);
   return 0;
}

/*
题目：
首先，这道题目是一道斐波那契数列的题目。
我们来分析一下，第三个图形是如何由前两个图形组成。
 ______           _______
|    | |   或    |  |____|
|____|_|         |__|____|

扩展到第n个图形，我们有：
 _____________           ______________
|           | |  或     |         |____|
|___________|_|         |_________|____|
所以，f(n)=f(n-1)+f(n-2)

由于n可能会很大，所以我们需要一些计算的技巧。
斐波那契数列是可以由矩阵计算得到，如下：

[a,b]* [0,1] = [b,a+b]
       [1,1]

令mat =[0,1]
       [1,1]

那么，理论上，我们乘以n个矩阵mat，就可以求得f(n)，
但是n个矩阵相乘，时间复杂度为O(n)，
这时候，我们采用快速幂运算来求解，可以把时间复杂度降为O(logn)。

*/

#include<string>
#include <iomanip>
#include<fstream>
#include<set>
#include<queue>
#include<map>
//#include<unordered_set>
//#include<unordered_map>
//#include <sstream>
//#include "func.h"
//#include <list>
#include<stdio.h>
#include<iostream>
#include<string>
#include<memory.h>
#include<limits.h>
//#include<stack>
#include<vector>
#include <algorithm>
using namespace std;
#define MOD 19999997
class matrix22
{
	public:
	long long a1, a2;
	long long  b1, b2;
	matrix22() :a1(0), a2(1), b1(1), b2(1){};
	matrix22 operator*(const matrix22 tmp)     // 重载矩阵乘法
	{
		matrix22 mat;
		mat.a1 = (a1%MOD)*(tmp.a1%MOD) + (a2%MOD)*(tmp.b1%MOD);
		mat.a2 = (a1%MOD)*(tmp.a2%MOD) + (a2%MOD)*(tmp.b2%MOD);
		mat.b1 = (b1%MOD)*(tmp.a1%MOD) + (b2%MOD)*(tmp.b1%MOD);
		mat.b2 = (b1%MOD)*(tmp.a2%MOD) + (b2%MOD)*(tmp.b2%MOD);
		return mat;
	}
};
/*
函数名  ：main
函数功能：主函数
*/
int main(void)
{
	int n;
	scanf("%d", &n);
	int dp1 = 1;
	int dp2 = 2;
	if (n <= 0) printf("0\n");
	else if (n == 1) printf("1\n");
	else if (n == 2) printf("2\n");
	else
	{
		n -= 3;
		matrix22 mat;
		matrix22 ans;
		while (n != 0)
		{
			//如果二进制该位为1，则ans*mat
			if (n & 1)
				ans = ans*mat;
			//mat每次与自身相乘，求得矩阵的1，2，4，8，16次方
			mat = mat*mat;
			n = (n >> 1);
		}
		//输出f(n)
		long long answer =( ans.a2 + 2 * ans.b2)%MOD;
		cout << answer << endl;

	}
	return  0;
}