多变量高斯（MVN）概率建模的两种方案

摘要：在我们的时序异常检测应用中，设计了对时序数据进行多变量高斯（MVN）建模的算法方案进行异常检测，本文对基于tensorflow的两种MVN建模方案进行了总结。

1、基于custom cholesky分解

基于tensorflow keras对多维数据进行多变量高斯（MVN）概率建模是可行的。方法是通过一个编码器网络对输入进行编码，再通过概率层网络将编码向量映射为MVN的均值向量μ和协方差矩阵Σ，并计算样本的概率密度值，通过最大化样本的概率密度（实际是通过最小化概率密度的负对数）可以完成模型的训练。

这里的核心问题是如何保证协方差矩阵Σ的对称正定性。对称性的保证十分简单，只需计算Σ的上三角或下三角矩阵，然后转置相加即可。而正定性的保证则要依赖于cholesky分解，cholesky分解讲的是，一个Hermitian正定阵A可以被分解为一个对角线元素为正实数的下三角阵L与其共轭转置L^*的乘积：A=LL^*。反之也成立：如果A可以被分解为LL^*，那么A是一个Hermitian正定矩阵。在实矩阵的语境下，cholesky分解即，一个对称正定实矩阵可以分解为一个对角线元素全部为正的下三角矩阵及其转置的乘积：A=LL^T。

基于cholesky分解，在概率层，要将编码向量映射为一个正定对称阵就容易了。只须首先将编码向量映射为一个正定下三角矩阵（只需保证对角线元素非负），然后根据cholesky分解即可得到一个正定对称矩阵。考虑到MVN的形式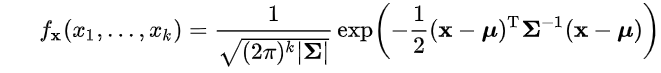，实际我们在概率层并不直接将编码向量映射为Σ矩阵，而是将其映射为precision矩阵（Σ的逆），而保证precision矩阵的正定性与保证Σ的正定性是一致的。

以上正是在我们的IoT设备异常检测应用中所设计和采用的算法。

2、基于tensorflow probability

后来通过调研，发现了一个十分强大的概率建模工具：tensorflow probability。tensorflow probability layers的MultivariateNormTril模块就是一个MVN概率建模模块，通过使用该模块，用户无须自己实现复杂的cholesky语义，即可完成MVN建模。

以下是基于MultivariateNormTril建模的一个例子：

tfk = tf.keras
tfkl = tf.keras.layers
tfd = tfp.distributions
tfpl = tfp.layers

# Load data.
n = int(1e3)
scale_tril = np.array([[1.6180, 0.],
                       [-2.7183, 3.1416]]).astype(np.float32)
x = tfd.Normal(loc=0, scale=1).sample([n, 2])
eps = tfd.Normal(loc=0, scale=0.01).sample([n, 2])
y = tf.matmul(x, scale_tril) + eps

# Create model.
d = tf.dimension_value(y.shape[-1])
model = tfk.Sequential([
    tfkl.Dense(tfpl.MultivariateNormalTriL.params_size(d)),
    tfpl.MultivariateNormalTriL(d),
])

# Fit.
model.compile(optimizer=tf.train.AdamOptimizer(learning_rate=0.02),
              loss=lambda y, model: -model.log_prob(y),
              metrics=[])
batch_size = 100
model.fit(x, y,
          batch_size=batch_size,
          epochs=500,
          steps_per_epoch=n // batch_size,
          verbose=True,
          shuffle=True)
model.get_weights()[0][:, :2]
# ==> [[  1.61842895e+00   1.34138885e-04]
#      [ -2.71818233e+00   3.14186454e+00]]