队列，一种"公平"的数据结构

路过一家奶茶店，由于生意火爆，门口的排着长长的队伍，先排队的人先买到奶茶，然后再轮到下一个，秩序井然。有没有一种数据结构能体现”先来后到“这种顺序呢？

当然有，那就是队列。先看一下定义：队列是一种操作受限的线性表，它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作。只能在表的最前端删除，最后端插入，这和排队买奶茶中先给最前面的人做奶茶，新来的只能在最后面排队一样，相对“公平”。

根据定义我们可以知道，队列主要支持两种操作，一种是删除（出队dequeue）操作，另一种是插入（入队enqueue）操作，它的一个主要特点是先进先出，这一定要记住

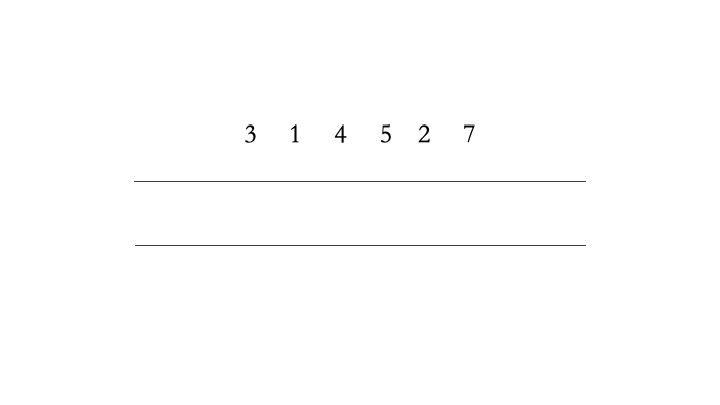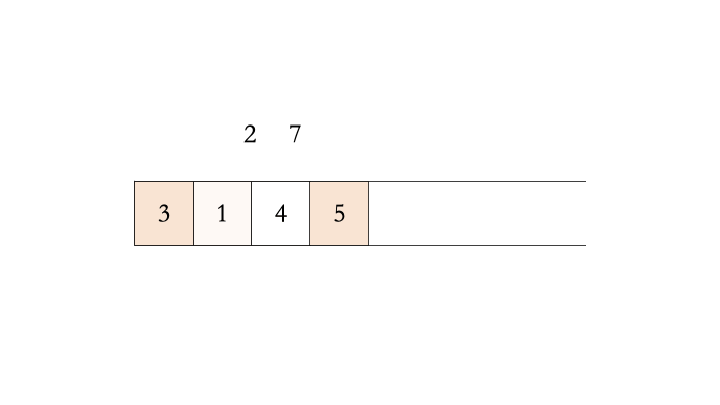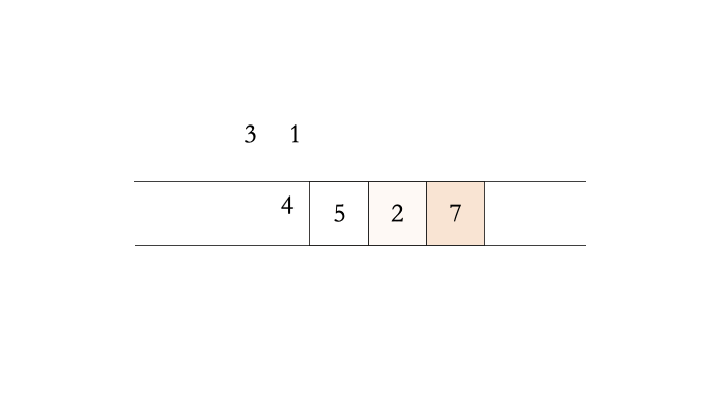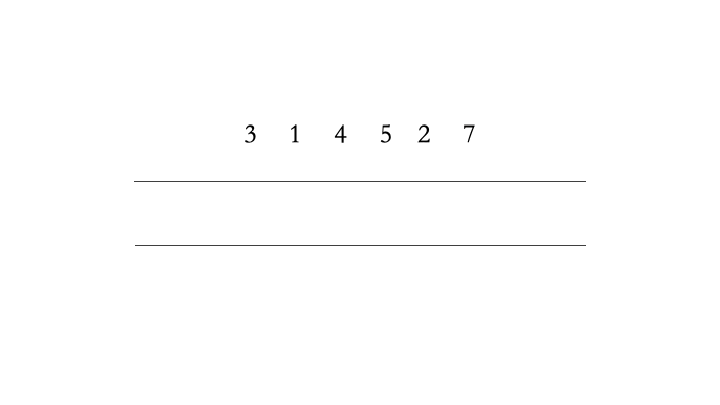
之前我们讲过”栈“，它和队列类似，也是一种操作受限的线性表，但它是”先进后出“，与队列相反。

队列的实现

和栈一样，它可以使用数组实现(顺序队列)，也可以使用链表实现(链式队列)。

顺序队列

    public class QueueArray<T>
    {
        //存储内容的泛型数组
        public T[] items;
​
        //数组长度
        private int len;
​
        //使用头指针和尾指针辅助入队、出队操作
        int head, tail = 0;
​
        public QueueArray(int capacity)
        {
            items = new T[capacity];
            len = capacity;
        }
​
        //入队
        public bool Enqueue(T val)
        {
            //尾指针与数组长度相同，说明队列已满，返回false（注意，该判断存在问题）
            if (tail == len)
                return false;
​
            items[tail++] = val;
​
            return true;
        }
​
        //出队
        public T Dequeue()
        {
            if (tail == head)
                throw new Exception("Queue is empty");
​
            return items[head++];
        }
    }

现在基本功能已经实现了，但仔细分析会发现，代码中的tail和head都只会向后移动(数量只会增加)，因此tail == len并不代表数组已满，因为数组头部的数据可能已经出队了，前面出现了许多空闲空间。如下图所示

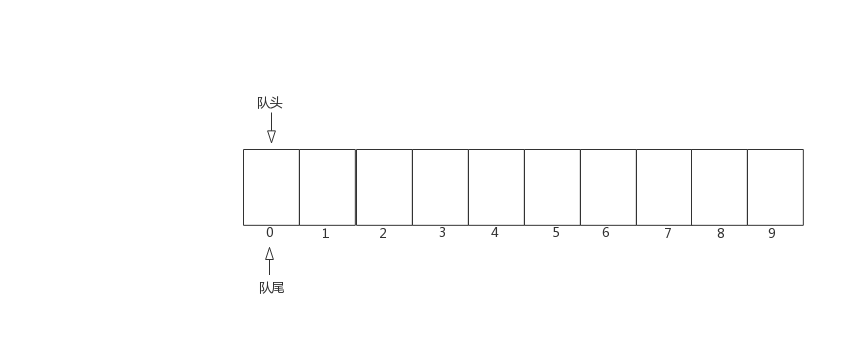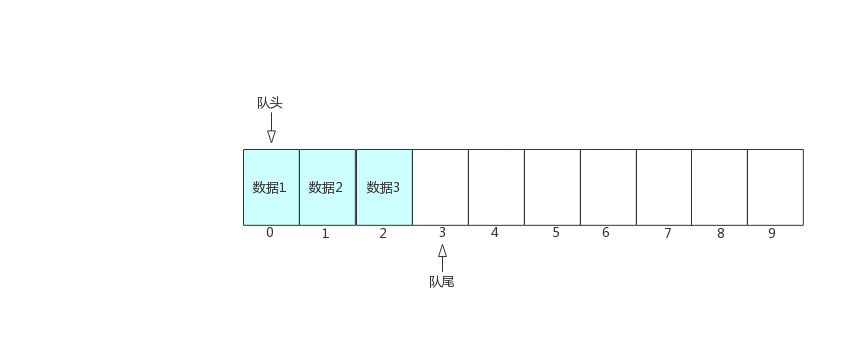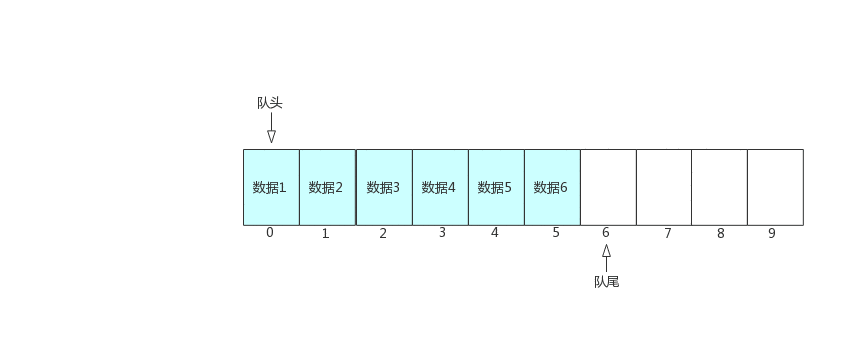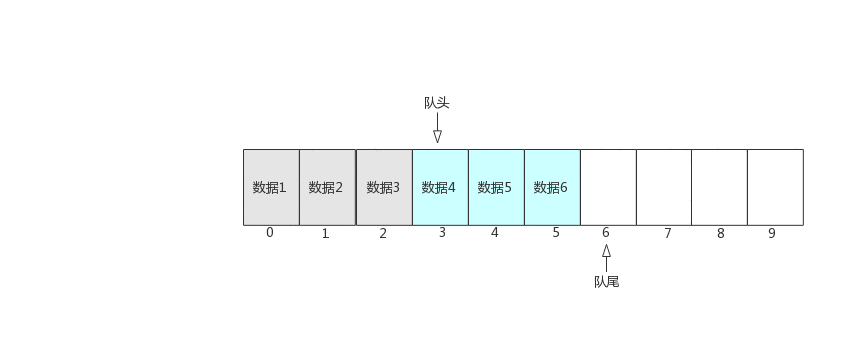
随着不停的执行入队、出队操作，即使数组中还有空闲空间，也无法继续往队列中添加数据了。此时，需要使用数据搬移，即将队列中的元素整体搬移到数组头，如下图所示。

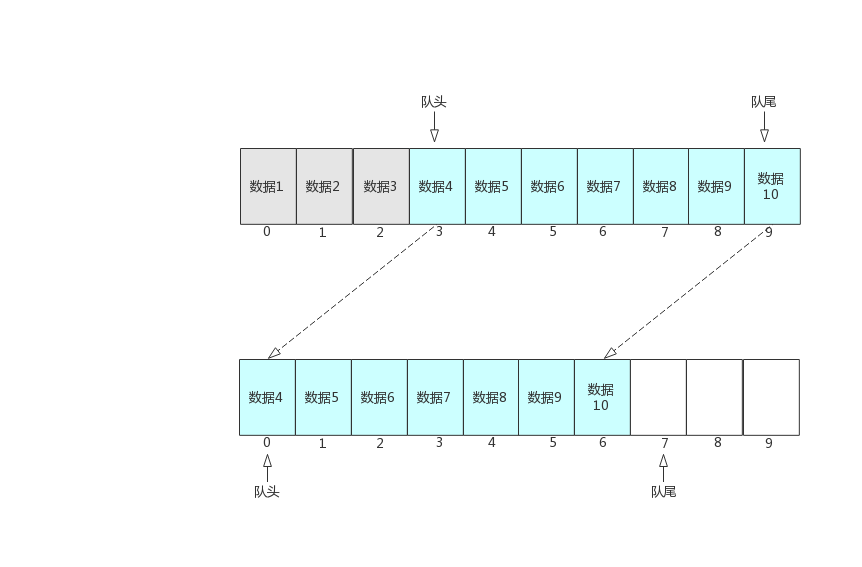
该操作只需要在入队并且”队列已满“的时候执行，因此我们需要修改Enqueue()的代码为

        //入队
        public bool Enqueue(T val)
        {
            if (tail == len)
            {
                // tail ==n && head==0，表示整个队列都占满了
                if (head == 0) return false;
                // 数据搬移
                for (int i = head; i < tail; ++i)
                {
                    items[i - head] = items[i];
                }
                // 搬移完之后重新更新head和tail
                tail -= head;
            }
​
            items[tail++] = val;
​
            return true;
        }

循环队列

循环队列也是基于数组实现的，并且能够很好的解决上面当tail==n需要数据搬移的问题（数据搬移会消耗许多性能）。

顾名思义，环形队列长得像是一个环，怎么将数组“变成”环呢？思路是当tail==n时，如果有空闲位置让tail = (tail + 1) % len，即将尾部指针转移到数组头部来开始新的循环，这样修改最关键的就是要正确判断队空和队满的条件。下图中蓝色代表头指针，红色代表尾指针

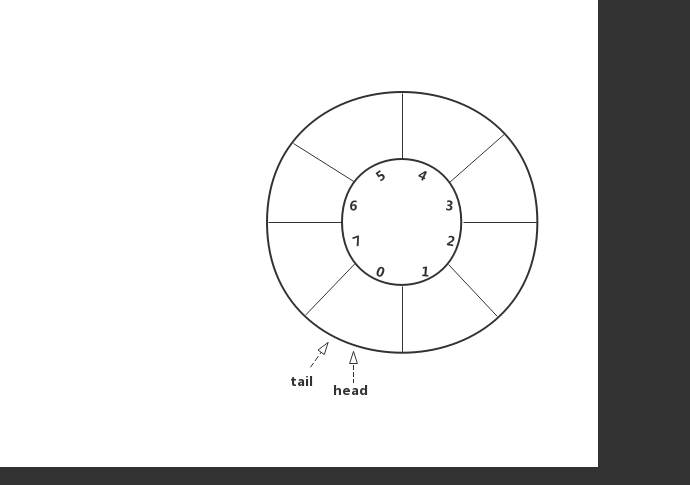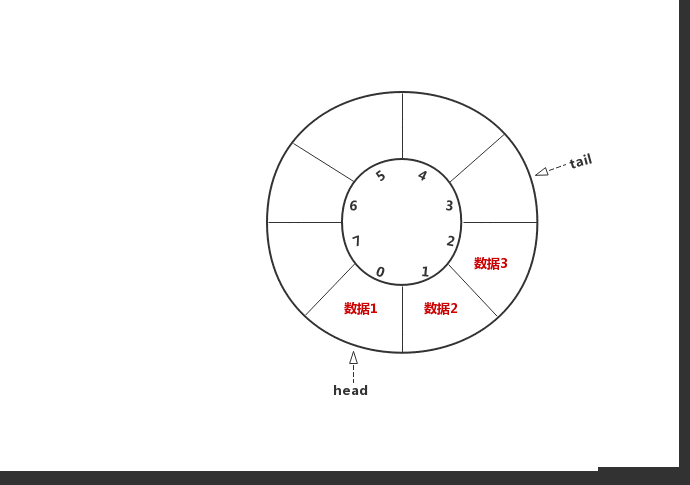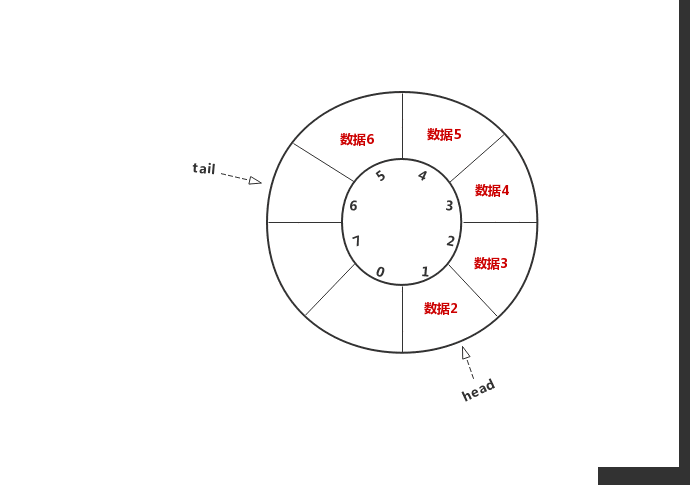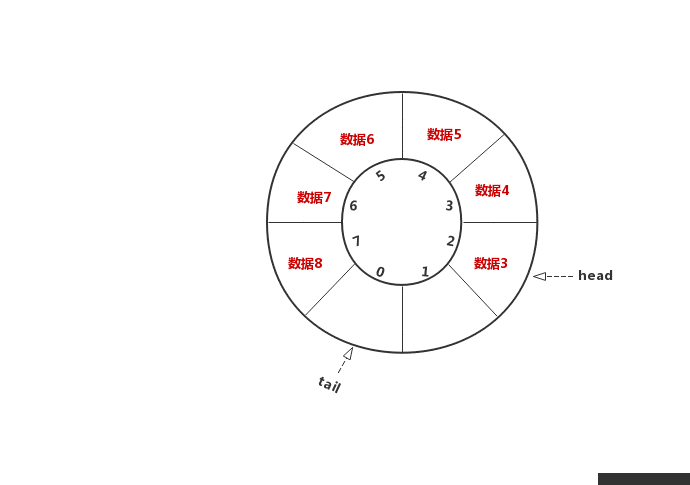
修改入队和出队的代码

        //入队
        public bool Enqueue(T val)
        {
            //使用尾指针与头指针来判断队列是否满
            if ((tail + 1) % len == head)
                return false;
​
            items[tail] = val;
            tail = (tail + 1) % len;
            return true;
        }
​
        //出队
        public T Dequeue()
        {
            if (tail == head)
                throw new Exception("Queue is empty");
​
            T ans = items[head]; 
            head = (head + 1) % len; 
            return ans;
        }

因为判断队满使用的是(tail+1)%n=head，所以当队列满时，tail指向的位置实际上是没有存储数据的，浪费了数组的一个存储空间。

‍♂ 代码虽然不多，但最好能够自己手动实现

链式队列

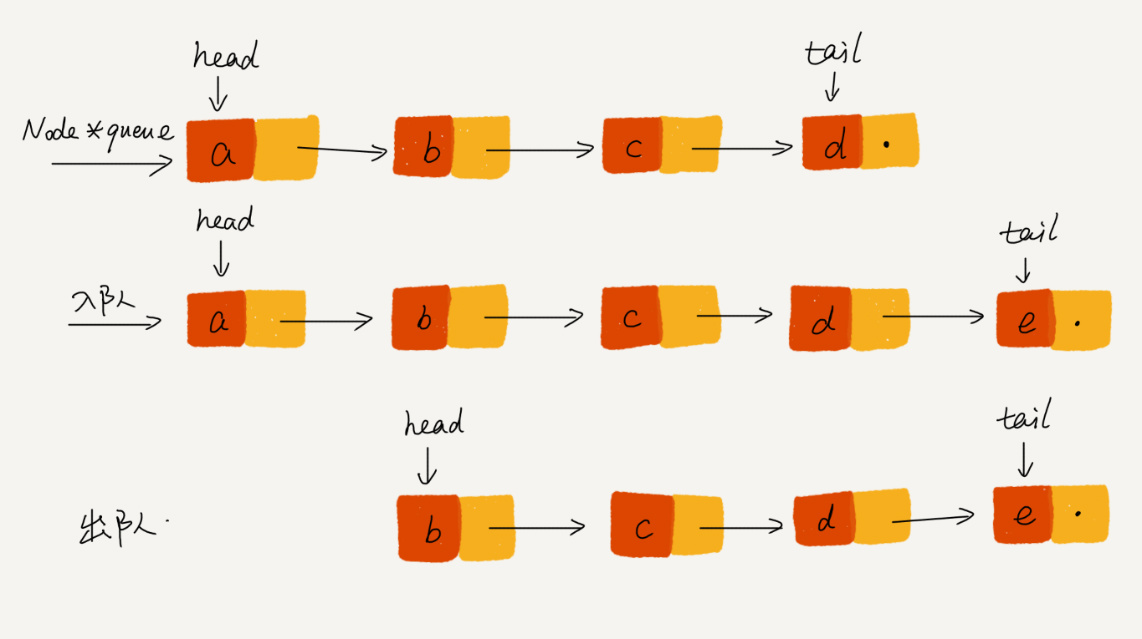
基于链表的实现，我们同样需要两个指针：head 指针和 tail 指针。它们分别指向链表的第一个结点和最后一个结点。如图所示，入队时，tail->next= new_node, tail = tail->next；出队时，head = head->next，实现起来比较简单，这里就省略了

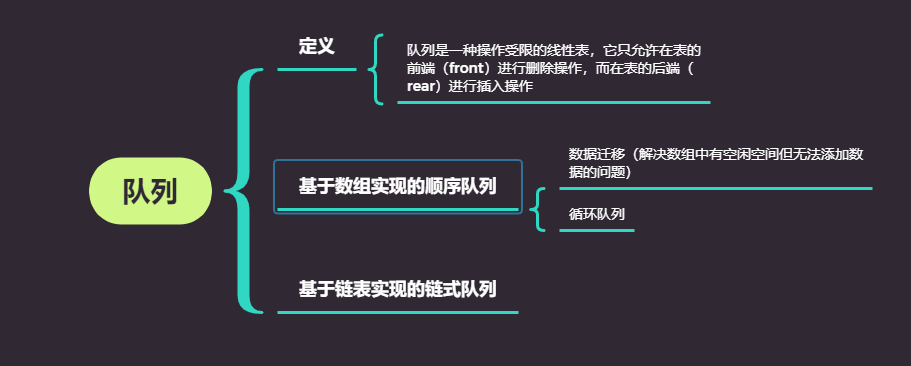
总结