Sequence Model-week3编程题1-Neural Machine Translation with Attention
1. Neural Machine Translation
下面将构建一个神经机器翻译(NMT)模型,将人类可读日期 ("25th of June, 2009") 转换为机器可读日期 ("2009-06-25").
使用 attention model.
from keras.layers import Bidirectional, Concatenate, Permute, Dot, Input, LSTM, Multiply
from keras.layers import RepeatVector, Dense, Activation, Lambda
from keras.optimizers import Adam
from keras.utils import to_categorical
from keras.models import load_model, Model
import keras.backend as K
import numpy as np
from faker import Faker
import random
from tqdm import tqdm
from babel.dates import format_date
from nmt_utils import *
import matplotlib.pyplot as plt
%matplotlib inline
2. 人类可读日期转机器可读日期(Translating human readable dates into machine readable dates)
你将在这里构建的模型可以用于从一种语言翻译到另一种语言,例如从英语翻译到印地语。
然而,语言翻译需要大量的数据集,通常需要几天的GPU训练。
我们将执行一个更简单的 “日期翻译” 任务。
该网络将输入以各种可能的格式编写的日期(e.g. "the 29th of August 1958", "03/30/1968", "24 JUNE 1987")
该网络将翻译他们为标准化的机器可读日期 (e.g. "1958-08-29", "1968-03-30", "1987-06-24").(YYYY-MM-DD)
2.1 Dataset
我们将在10,000个人类可读日期 及其 等效、标准化、机器可读日期的数据集上对模型进行培训。 加载数据集:
m = 10000
dataset, human_vocab, machine_vocab, inv_machine_vocab = load_dataset(m)
print(dataset[:10])
print(human_vocab, len(human_vocab))
print(machine_vocab, len(machine_vocab))
[('tuesday january 31 2006', '2006-01-31'), ('20 oct 1986', '1986-10-20'), ('25 february 2008', '2008-02-25'), ('sunday november 11 1984', '1984-11-11'), ('20.06.72', '1972-06-20'), ('august 9 1983', '1983-08-09'), ('march 30 1993', '1993-03-30'), ('10 jun 2017', '2017-06-10'), ('december 21 2001', '2001-12-21'), ('monday october 11 1999', '1999-10-11')]
{' ': 0, '.': 1, '/': 2, '0': 3, '1': 4, '2': 5, '3': 6, '4': 7, '5': 8, '6': 9, '7': 10, '8': 11, '9': 12, 'a': 13, 'b': 14, 'c': 15, 'd': 16, 'e': 17, 'f': 18, 'g': 19, 'h': 20, 'i': 21, 'j': 22, 'l': 23, 'm': 24, 'n': 25, 'o': 26, 'p': 27, 'r': 28, 's': 29, 't': 30, 'u': 31, 'v': 32, 'w': 33, 'y': 34, '<unk>': 35, '<pad>': 36} 37
{'-': 0, '0': 1, '1': 2, '2': 3, '3': 4, '4': 5, '5': 6, '6': 7, '7': 8, '8': 9, '9': 10} 11
dataset: 一个元组列表 (人类可读日期, 机器可读日期)。human_vocab: 一个python字典,将人类可读日期中使用的所有字符 映射到 整数值索引。machine_vocab: 一个python字典,将机器可读日期中使用的所有字符 映射到 整数值索引。这些索引不一定与 human_vocab 的索引一致。inv_machine_vocab: machine_vocab的逆字典,从索引到字符的映射。
2.2 预处理数据
设置 Tx=30
我们假设 Tx 是人类可读日期的最大长度。
如果我们得到更长的输入,我们将不得不截断(truncate)它。
设置 Ty=10
- "YYYY-MM-DD" 是 10 characters 长度.
Tx = 30
Ty = 10
X, Y, Xoh, Yoh = preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty)
print("X.shape:", X.shape)
print("Y.shape:", Y.shape)
print("Xoh.shape:", Xoh.shape)
print("Yoh.shape:", Yoh.shape)
X.shape: (10000, 30)
Y.shape: (10000, 10)
Xoh.shape: (10000, 30, 37)
Yoh.shape: (10000, 10, 11)
你现在有:
X: 训练集中 人类可读日期 的处理版本.其中每个字符都被它在
human_vocab中映射该字符的索引替换. 89%每个日期都使用特殊字符(< pad >)进一步填充,确保 T_x 长度.
X.shape = (m, Tx)where m is the number of training examples in a batch.
Y: 训练集中 机器可读日期 的处理版本其中每个字符都被它在
machine_vocab中映射的索引替换.Y.shape = (m, Ty).
Xoh:X的 one-hot版本one-hot 中条目 “1” 的索引被映射到在
human_vocab中对应字符. (如果 index is 2, one-hot 版本:[0,0,1,0,0,...,0]Xoh.shape = (m, Tx, len(human_vocab))
Yoh:Y的 one-hot版本one-hot 中条目 “1” 的索引被映射到在
machine_vocab中对应字符.Yoh.shape = (m, Tx, len(machine_vocab)).len(machine_vocab) = 11由于有 10 数字(0-9) 和-符号.
index = 0
print("Source date:", dataset[index][0])
print("Target date:", dataset[index][1])
print()
print("Source after preprocessing (indices):", X[index])
print("Target after preprocessing (indices):", Y[index])
print()
print("Source after preprocessing (one-hot):", Xoh[index]) # 每行是一个T_t的输出,输出的是对应相应字符的一个one-hot向量.
print("Target after preprocessing (one-hot):", Yoh[index])
Source date: tuesday january 31 2006
Target date: 2006-01-31
Source after preprocessing (indices): [30 31 17 29 16 13 34 0 22 13 25 31 13 28 34 0 6 4 0 5 3 3 9 36 36
36 36 36 36 36]
Target after preprocessing (indices): [3 1 1 7 0 1 2 0 4 2]
Source after preprocessing (one-hot): [[ 0. 0. 0. ..., 0. 0. 0.]
[ 0. 0. 0. ..., 0. 0. 0.]
[ 0. 0. 0. ..., 0. 0. 0.]
...,
[ 0. 0. 0. ..., 0. 0. 1.]
[ 0. 0. 0. ..., 0. 0. 1.]
[ 0. 0. 0. ..., 0. 0. 1.]]
Target after preprocessing (one-hot): [[ 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
[ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]]
3. Neural machine translation with attention
如果你必须把一本书的段落从法语翻译成英语,你就不会读整个段落,然后关闭这本书并翻译。
即使在翻译过程中,你也会阅读/重读,并专注于法语段落中与你正在写的英语部分相对应的部分
注意机制告诉神经机器翻译模型,它应该注意任何步骤。
3.1 Attention mechanism
工作原理:
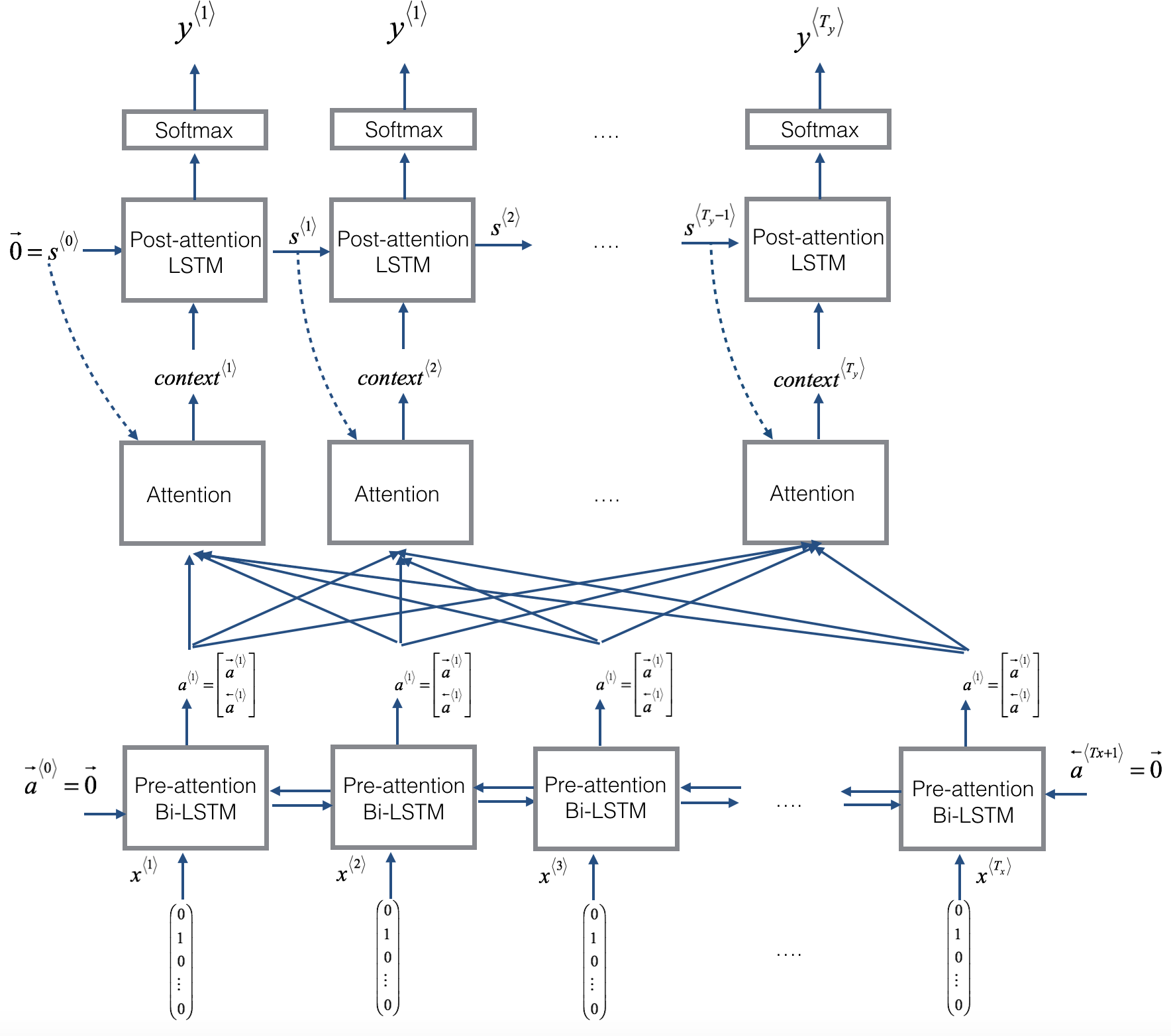
左图显示了 attention model.
右图显示了 一个 "attention" 步骤 用来计算 attention 变量 \(\alpha^{\langle t, t' \rangle}\).
Attention 变量 \(\alpha^{\langle t, t' \rangle}\) 用于计算输出中每个时间步(\(t=1, \ldots, T_y\)) 的上下文变量 \(context^{\langle t \rangle}\) (\(C^{\langle t \rangle}\)).
 |
 |
**Figure 1**: Neural machine translation with attention
以下是您可能要注意的模型的一些属性:
Pre-attention and Post-attention LSTMs 在the attention mechanism 两边
模型中有两个单独的 LSTM(见左图): pre-attention and post-attention LSTMs.
Pre-attention Bi-LSTM 在图片底部 是 一个 Bi-directional LSTM(双向LSTM) 在 attention mechanism 之前.
The attention mechanism 是左图中间的部分(Attention).
The pre-attention Bi-LSTM 穿过 \(T_x\) time steps
Post-attention LSTM: 在图片顶部 在 attention mechanism 之后.
The post-attention LSTM 穿过 \(T_y\) time steps.
The post-attention LSTM 通过 hidden state \(s^{\langle t \rangle}\) 和 cell state \(c^{\langle t \rangle}\) 从一个time step 到 另一个time step.
An LSTM 有一个 hidden state 和 cell state
对于post-attention sequence model 我们仅使用了基本的 RNN
- 这意味着,RNN捕获的the state 只输出 hidden state \(s^{\langle t\rangle}\).
这个任务中, 我们使用一个LSTM 代替基本RNN.
- 因此,LSTM 有 hidden state \(s^{\langle t\rangle}\), 也有 cell state \(c^{\langle t\rangle}\).
每个time step 不使用前一个time step的预测
与之前的文本生成示例(例如第1周的Dinosaurus)不同, 在此模型中, post-activation LSTM 在时间 \(t\) 不会用具体生成的 预测 \(y^{\langle t-1 \rangle}\) 作为输入.
post-attention LSTM 在 time 't' 只需要 hidden state \(s^{\langle t\rangle}\) 和 cell state \(c^{\langle t\rangle}\) 作为输入.
我们以这种方式设计了模型,因为(与相邻字符高度相关的语言生成不同) 在YYYY-MM-DD日期中, 前一个字符与下一个字符之间的依赖性不强。
Concatenation(连接) of hidden states(\(a^{\langle t\rangle}\)) 来自 前向(forward) 和 后向(backward) pre-attention LSTMs
\(\overrightarrow{a}^{\langle t \rangle}\): hidden state of the forward-direction, pre-attention LSTM.
\(\overleftarrow{a}^{\langle t \rangle}\): hidden state of the backward-direction, pre-attention LSTM.
\(a^{\langle t \rangle} = [\overrightarrow{a}^{\langle t \rangle}, \overleftarrow{a}^{\langle t \rangle}]\): the concatenation of the activations of both the forward-direction \(\overrightarrow{a}^{\langle t \rangle}\) and backward-directions \(\overleftarrow{a}^{\langle t \rangle}\) of the pre-attention Bi-LSTM.
Computing "energies" \(e^{\langle t, t' \rangle}\) as a function of \(s^{\langle t-1 \rangle}\) and \(a^{\langle t' \rangle}\)
Recall in the lesson videos "Attention Model", at time 6:45 to 8:16, the definition of "e" as a function of \(s^{\langle t-1 \rangle}\) and \(a^{\langle t \rangle}\).
"e" is called the "energies" variable.
\(s^{\langle t-1 \rangle}\) is the hidden state of the post-attention LSTM
\(a^{\langle t' \rangle}\) is the hidden state of the pre-attention LSTM.
\(s^{\langle t-1 \rangle}\) and \(a^{\langle t \rangle}\) are fed into a simple neural network, which learns the function to output \(e^{\langle t, t' \rangle}\).
\(e^{\langle t, t' \rangle}\) is then used when computing the attention \(a^{\langle t, t' \rangle}\) that \(y^{\langle t \rangle}\) should pay to \(a^{\langle t' \rangle}\).
右图使用了一个
RepeatVectornode to copy \(s^{\langle t-1 \rangle}\)'s value \(T_x\) times.然后,它使用
Concatenation来连接(concatenate) \(s^{\langle t-1 \rangle}\) 和 \(a^{\langle t \rangle}\).The concatenation of \(s^{\langle t-1 \rangle}\) and \(a^{\langle t \rangle}\) is fed into a "Dense" layer, 用来计算 \(e^{\langle t, t' \rangle}\).
\(e^{\langle t, t' \rangle}\) is then passed through a softmax to compute \(\alpha^{\langle t, t' \rangle}\).
变量 \(e^{\langle t, t' \rangle}\)图中没有显示给出, 但是 \(e^{\langle t, t' \rangle}\) 在 the Dense layer 和 the Softmax layer 之间(图右).
将解释如何在Keras使用
RepeatVectorandConcatenation.
3.2 Implement Details
实现 neural translator,你将实现两个函数:one_step_attention() and model().
3.21 one_step_attention
The inputs to the one_step_attention at time step \(t\) are:
\([a^{<1>},a^{<2>}, ..., a^{<T_x>}]\): all hidden states of the pre-attention Bi-LSTM.
\(s^{<t-1>}\): the previous hidden state of the post-attention LSTM.
one_step_attention computes:
\([\alpha^{<t,1>},\alpha^{<t,2>}, ..., \alpha^{<t,T_x>}]\): the attention weights
\(context^{ \langle t \rangle }\): the context vector:
\]
Clarifying 'context' and 'c'
the context 用 \(c^{\langle t \rangle}\) 来表示.
这个任务中, 我们将 the context 用 \(context^{\langle t \rangle}\) 表示.
- 这是为了避免与 the post-attention LSTM's 内部存储单元变量(internal memory cell)混淆, 该变量用 \(c^{\langle t \rangle}\) 表示.
实现 one_step_attention
Exercise: 实现 one_step_attention().
这个函数
model()将使用for循环调用 the layers inone_step_attention()\(T_y\) .所有 \(T_y\) copies 要有相同的权重(weights).
不需要每次都重新初始化权重
所有 \(T_y\) steps 应该有共同的权重
下面是如何在Keras中实现具有可共享权重的层:
定义
one_step_attention函数之外的变量范围中的层对象。 例如,将对象定义为全局变量将有效- 注意,在函数
model的范围内 定义这些变量在技术上是可行的(为了方便)
- 注意,在函数
当传播输入时,调用这些对象
我们已将所需图层定义为全局变量
示例及文档:
-
var_repeated = repeat_layer(var1)
-
concatenated_vars = concatenate_layer([var1,var2,var3])
-
var_out = dense_layer(var_in)
-
- activation = activation_layer(var_in)
-
- dot_product = dot_layer([var1,var2])
-
# Defined shared layers as global variables
repeator = RepeatVector(Tx) # copy s^<t-1>'s value T_x times
concatenator = Concatenate(axis=-1) # 按行连接
densor1 = Dense(10, activation = "tanh")
densor2 = Dense(1, activation = "relu")
activator = Activation(softmax, name='attention_weights') # We are using a custom softmax(axis = 1) loaded in this notebook
dotor = Dot(axes = 1) # 计算 context
# GRADED FUNCTION: one_step_attention
def one_step_attention(a, s_prev):
"""
Performs one step of attention: Outputs a context vector computed as a dot product of the attention weights
"alphas" and the hidden states "a" of the Bi-LSTM.
Arguments:
a -- hidden state output of the Bi-LSTM, numpy-array of shape (m, Tx, 2*n_a)
s_prev -- previous hidden state of the (post-attention) LSTM, numpy-array of shape (m, n_s)
Returns:
context -- context vector, input of the next (post-attention) LSTM cell
"""
### START CODE HERE ###
# Use repeator to repeat s_prev to be of shape (m, Tx, n_s) so that you can concatenate it with all hidden states "a" (≈ 1 line)
s_prev = repeator(s_prev)
# Use concatenator to concatenate a and s_prev on the last axis (≈ 1 line)
# For grading purposes, please list 'a' first and 's_prev' second, in this order.
concat = concatenator([a, s_prev])
# Use densor1 to propagate concat through a small fully-connected neural network to compute the "intermediate energies" variable e. (≈1 lines)
e = densor1(concat)
# Use densor2 to propagate e through a small fully-connected neural network to compute the "energies" variable energies. (≈1 lines)
energies = densor2(e)
# Use "activator" on "energies" to compute the attention weights "alphas" (≈ 1 line)
alphas = activator(energies)
# Use dotor together with "alphas" and "a" to compute the context vector to be given to the next (post-attention) LSTM-cell (≈ 1 line)
context = Dot([alphas, a])
### END CODE HERE ###
return context
3.22 model
首先,
model通过 Bi-LSTM 运行输入,以获得 \([a^{<1>},a^{<2>}, ..., a^{<T_x>}]\).然后,
model用for循环调用one_step_attention()\(T_y\) times:它将计算 context vector \(context^{<t>}\) 传入 the post-attention LSTM.
它通过带有softmax activation的 dense layer 运行the post-attention 的输出.
The softmax 生成一个预测 \(\hat{y}^{<t>}\).
Exercise: 实现 model(),定义global layers,共享在model中使用的权重
n_a = 32 # number of units for the pre-attention, bi-directional LSTM's hidden state 'a'
n_s = 64 # number of units for the post-attention LSTM's hidden state "s"
# Please note, this is the post attention LSTM cell.
# For the purposes of passing the automatic grader
# please do not modify this global variable. This will be corrected once the automatic grader is also updated.
post_activation_LSTM_cell = LSTM(n_s, return_state = True) # post-attention LSTM
output_layer = Dense(len(machine_vocab), activation=softmax)
现在您可以在 for 循环中使用这些图层 \(T_y\) 次来生成输出,并且他们的参数不会重新初始化。您必须执行以下步骤:
- 传入输入参数
X到 Bi-directional LSTM.- Bidirectional
- LSTM
- 记住,我们希望LSTM返回一个完整的序列,而不仅仅是最后一个隐藏状态。
Sample code:
sequence_of_hidden_states = Bidirectional(LSTM(units=..., return_sequences=...))(the_input_X)
迭代 for \(t = 0, \cdots, T_y-1\):
调用
one_step_attention(),从 pre-attention bi-directional LSTM 传递 hidden states \([a^{\langle 1 \rangle},a^{\langle 2 \rangle}, ..., a^{ \langle T_x \rangle}]\) 的序列, 用来自 post-attention LSTM 的 previous hidden state \(s^{<t-1>}\) 来计算 context vector \(context^{<t>}\).使用 \(context^{<t>}\) 作为参数传给 post-attention LSTM cell.
- 记得传入这个LSTM以前的 hidden-state \(s^{\langle t-1\rangle}\) 和 cell-states \(c^{\langle t-1\rangle}\)
- 返回新的 hidden state \(s^{<t>}\) and 和 新的 cell state \(c^{<t>}\).
Sample code:
next_hidden_state, _ , next_cell_state =
post_activation_LSTM_cell(inputs=..., initial_state=[prev_hidden_state, prev_cell_state])
应用一个 dense, softmax layer 到 \(s^{<t>}\),获得输出
Sample code:output = output_layer(inputs=...)
通过将输出添加到输出列表来保存
创建您的Keras模型实例
它应该有三个输入:
X, the one-hot encoded inputs to the model, of shape (\(T_{x}, humanVocabSize)\)\(s^{\langle 0 \rangle}\), the initial hidden state of the post-attention LSTM
\(c^{\langle 0 \rangle}\), the initial cell state of the post-attention LSTM
The output is the list of outputs.
Sample code
model = Model(inputs=[...,...,...], outputs=...)
# GRADED FUNCTION: model
def model(Tx, Ty, n_a, n_s, human_vocab_size, machine_vocab_size):
"""
Arguments:
Tx -- length of the input sequence
Ty -- length of the output sequence
n_a -- hidden state size of the Bi-LSTM
n_s -- hidden state size of the post-attention LSTM
human_vocab_size -- size of the python dictionary "human_vocab"
machine_vocab_size -- size of the python dictionary "machine_vocab"
Returns:
model -- Keras model instance
"""
# Define the inputs of your model with a shape (Tx,)
# Define s0 and c0, initial hidden state for the decoder LSTM of shape (n_s,)
X = Input(shape=(Tx, human_vocab_size))
s0 = Input(shape=(n_s,), name='s0')
c0 = Input(shape=(n_s,), name='c0')
s = s0
c = c0
# Initialize empty list of outputs
outputs = []
### START CODE HERE ###
# Step 1: Define your pre-attention Bi-LSTM. Remember to use return_sequences=True. (≈ 1 line)
a = Bidirectional(LSTM(n_a,return_sequences=True))(X)
# Step 2: Iterate for Ty steps
for t in range(Ty):
# Step 2.A: Perform one step of the attention mechanism to get back the context vector at step t (≈ 1 line)
context = one_step_attention(a, s)
# Step 2.B: Apply the post-attention LSTM cell to the "context" vector.
# Don't forget to pass: initial_state = [hidden state, cell state] (≈ 1 line)
s, _, c = post_activation_LSTM_cell(context, initial_state=[s, c])
# Step 2.C: Apply Dense layer to the hidden state output of the post-attention LSTM (≈ 1 line)
out = output_layer(s)
# Step 2.D: Append "out" to the "outputs" list (≈ 1 line)
outputs.append(out)
# Step 3: Create model instance taking three inputs and returning the list of outputs. (≈ 1 line)
model = Model([X, s0, c0], outputs)
### END CODE HERE ###
return model
model = model(Tx, Ty, n_a, n_s, len(human_vocab), len(machine_vocab))
model.summary()
____________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_6 (InputLayer) (None, 30, 37) 0
____________________________________________________________________________________________________
s0 (InputLayer) (None, 64) 0
____________________________________________________________________________________________________
bidirectional_6 (Bidirectional) (None, 30, 64) 17920 input_6[0][0]
____________________________________________________________________________________________________
repeat_vector_1 (RepeatVector) (None, 30, 64) 0 s0[0][0]
lstm_9[0][0]
lstm_9[1][0]
lstm_9[2][0]
lstm_9[3][0]
lstm_9[4][0]
lstm_9[5][0]
lstm_9[6][0]
lstm_9[7][0]
lstm_9[8][0]
____________________________________________________________________________________________________
concatenate_1 (Concatenate) (None, 30, 128) 0 bidirectional_6[0][0]
repeat_vector_1[14][0]
bidirectional_6[0][0]
repeat_vector_1[15][0]
bidirectional_6[0][0]
repeat_vector_1[16][0]
bidirectional_6[0][0]
repeat_vector_1[17][0]
bidirectional_6[0][0]
repeat_vector_1[18][0]
bidirectional_6[0][0]
repeat_vector_1[19][0]
bidirectional_6[0][0]
repeat_vector_1[20][0]
bidirectional_6[0][0]
repeat_vector_1[21][0]
bidirectional_6[0][0]
repeat_vector_1[22][0]
bidirectional_6[0][0]
repeat_vector_1[23][0]
____________________________________________________________________________________________________
dense_1 (Dense) (None, 30, 10) 1290 concatenate_1[14][0]
concatenate_1[15][0]
concatenate_1[16][0]
concatenate_1[17][0]
concatenate_1[18][0]
concatenate_1[19][0]
concatenate_1[20][0]
concatenate_1[21][0]
concatenate_1[22][0]
concatenate_1[23][0]
____________________________________________________________________________________________________
dense_2 (Dense) (None, 30, 1) 11 dense_1[13][0]
dense_1[14][0]
dense_1[15][0]
dense_1[16][0]
dense_1[17][0]
dense_1[18][0]
dense_1[19][0]
dense_1[20][0]
dense_1[21][0]
dense_1[22][0]
____________________________________________________________________________________________________
attention_weights (Activation) (None, 30, 1) 0 dense_2[13][0]
dense_2[14][0]
dense_2[15][0]
dense_2[16][0]
dense_2[17][0]
dense_2[18][0]
dense_2[19][0]
dense_2[20][0]
dense_2[21][0]
dense_2[22][0]
____________________________________________________________________________________________________
dot_1 (Dot) (None, 1, 64) 0 attention_weights[13][0]
bidirectional_6[0][0]
attention_weights[14][0]
bidirectional_6[0][0]
attention_weights[15][0]
bidirectional_6[0][0]
attention_weights[16][0]
bidirectional_6[0][0]
attention_weights[17][0]
bidirectional_6[0][0]
attention_weights[18][0]
bidirectional_6[0][0]
attention_weights[19][0]
bidirectional_6[0][0]
attention_weights[20][0]
bidirectional_6[0][0]
attention_weights[21][0]
bidirectional_6[0][0]
attention_weights[22][0]
bidirectional_6[0][0]
____________________________________________________________________________________________________
c0 (InputLayer) (None, 64) 0
____________________________________________________________________________________________________
lstm_9 (LSTM) [(None, 64), (None, 6 33024 dot_1[13][0]
s0[0][0]
c0[0][0]
dot_1[14][0]
lstm_9[0][0]
lstm_9[0][2]
dot_1[15][0]
lstm_9[1][0]
lstm_9[1][2]
dot_1[16][0]
lstm_9[2][0]
lstm_9[2][2]
dot_1[17][0]
lstm_9[3][0]
lstm_9[3][2]
dot_1[18][0]
lstm_9[4][0]
lstm_9[4][2]
dot_1[19][0]
lstm_9[5][0]
lstm_9[5][2]
dot_1[20][0]
lstm_9[6][0]
lstm_9[6][2]
dot_1[21][0]
lstm_9[7][0]
lstm_9[7][2]
dot_1[22][0]
lstm_9[8][0]
lstm_9[8][2]
____________________________________________________________________________________________________
dense_6 (Dense) (None, 11) 715 lstm_9[0][0]
lstm_9[1][0]
lstm_9[2][0]
lstm_9[3][0]
lstm_9[4][0]
lstm_9[5][0]
lstm_9[6][0]
lstm_9[7][0]
lstm_9[8][0]
lstm_9[9][0]
====================================================================================================
Total params: 52,960
Trainable params: 52,960
Non-trainable params: 0
3.23 Compile the model
- 编译模型,定义 the loss function, optimizer and metrics you want to use.
Sample code
optimizer = Adam(lr=..., beta_1=..., beta_2=..., decay=...)
model.compile(optimizer=..., loss=..., metrics=[...])
### START CODE HERE ### (≈2 lines)
opt = Adam(lr = 0.005, beta_1=0.9, beta_2=0.999, decay=0.01)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
### END CODE HERE ###
3.24 定义输入和输出,fit the model
最后,定义all your inputs and outputs to fit the model:
输入 X of shape \((m = 10000, T_x = 30)\) 包含训练样本.
你需要创建
s0andc0,用 0 初始化你的post_attention_LSTM_cell.鉴于
model(),你需要 10个shape为 (m, T_y) 的元素列表。- The list
outputs[i][0], ..., outputs[i][Ty]represents the true labels (characters) corresponding to the \(i^{th}\) training example (X[i]). outputs[i][j]is the true label of the \(j^{th}\) character in the \(i^{th}\) training example.
- The list
s0 = np.zeros((m, n_s))
c0 = np.zeros((m, n_s))
outputs = list(Yoh.swapaxes(0,1))
model.fit([Xoh, s0, c0], outputs, epochs=1, batch_size=100)
Epoch 1/1
10000/10000 [==============================] - 58s - loss: 17.3019 - dense_6_loss_1: 1.4172 - dense_6_loss_2: 1.1897 - dense_6_loss_3: 1.8663 - dense_6_loss_4: 2.7026 - dense_6_loss_5: 0.8580 - dense_6_loss_6: 1.3185 - dense_6_loss_7: 2.7068 - dense_6_loss_8: 0.9499 - dense_6_loss_9: 1.7128 - dense_6_loss_10: 2.5801 - dense_6_acc_1: 0.3691 - dense_6_acc_2: 0.6124 - dense_6_acc_3: 0.2755 - dense_6_acc_4: 0.0813 - dense_6_acc_5: 0.9209 - dense_6_acc_6: 0.3072 - dense_6_acc_7: 0.0552 - dense_6_acc_8: 0.8989 - dense_6_acc_9: 0.2514 - dense_6_acc_10: 0.1004
在训练时,您可以看到输出的10个位置中的每个位置的损失以及准确性。
下表给出了一个例子,如果批处理有两个例子,那么精度可能是什么:

因此,dense_2_acc_8:0.89 表示您在当前批量数据中,89%的时间正确预测输出了第7个字符。
运行这个模型更长时间,并保存了权重:
model.load_weights('models/model.h5')
预测结果:
EXAMPLES = ['3 May 1979', '5 April 09', '21th of August 2016', 'Tue 10 Jul 2007', 'Saturday May 9 2018', 'March 3 2001', 'March 3rd 2001', '1 March 2001']
for example in EXAMPLES:
source = string_to_int(example, Tx, human_vocab)
source = np.array(list(map(lambda x: to_categorical(x, num_classes=len(human_vocab)), source))).swapaxes(0,1)
prediction = model.predict([source, s0, c0])
prediction = np.argmax(prediction, axis = -1)
output = [inv_machine_vocab[int(i)] for i in prediction]
print("source:", example)
print("output:", ''.join(output),"\n")
source: 3 May 1979
output: 1979-05-03
source: 5 April 09
output: 2009-05-05
source: 21th of August 2016
output: 2016-08-21
source: Tue 10 Jul 2007
output: 2007-07-10
source: Saturday May 9 2018
output: 2018-05-09
source: March 3 2001
output: 2001-03-03
source: March 3rd 2001
output: 2001-03-03
source: 1 March 2001
output: 2001-03-01
4. Visualizing Attention
由于该问题的输出长度固定为10,因此也可以使用10个不同的Softmax单元来生成输出的10个字符来执行此任务。
但是attention模型的一个优点是,输出的每个部分(例如月份)都知道它只需要依赖于输入的一小部分(输入中的字符给出月份), 我们可以可视化输出的每一部分是看输入的哪一部分。
考虑翻译 "Saturday 9 May 2018" to "2018-05-09" 工作. 如果我们可视化计算 \(\alpha^{\langle t, t' \rangle}\):
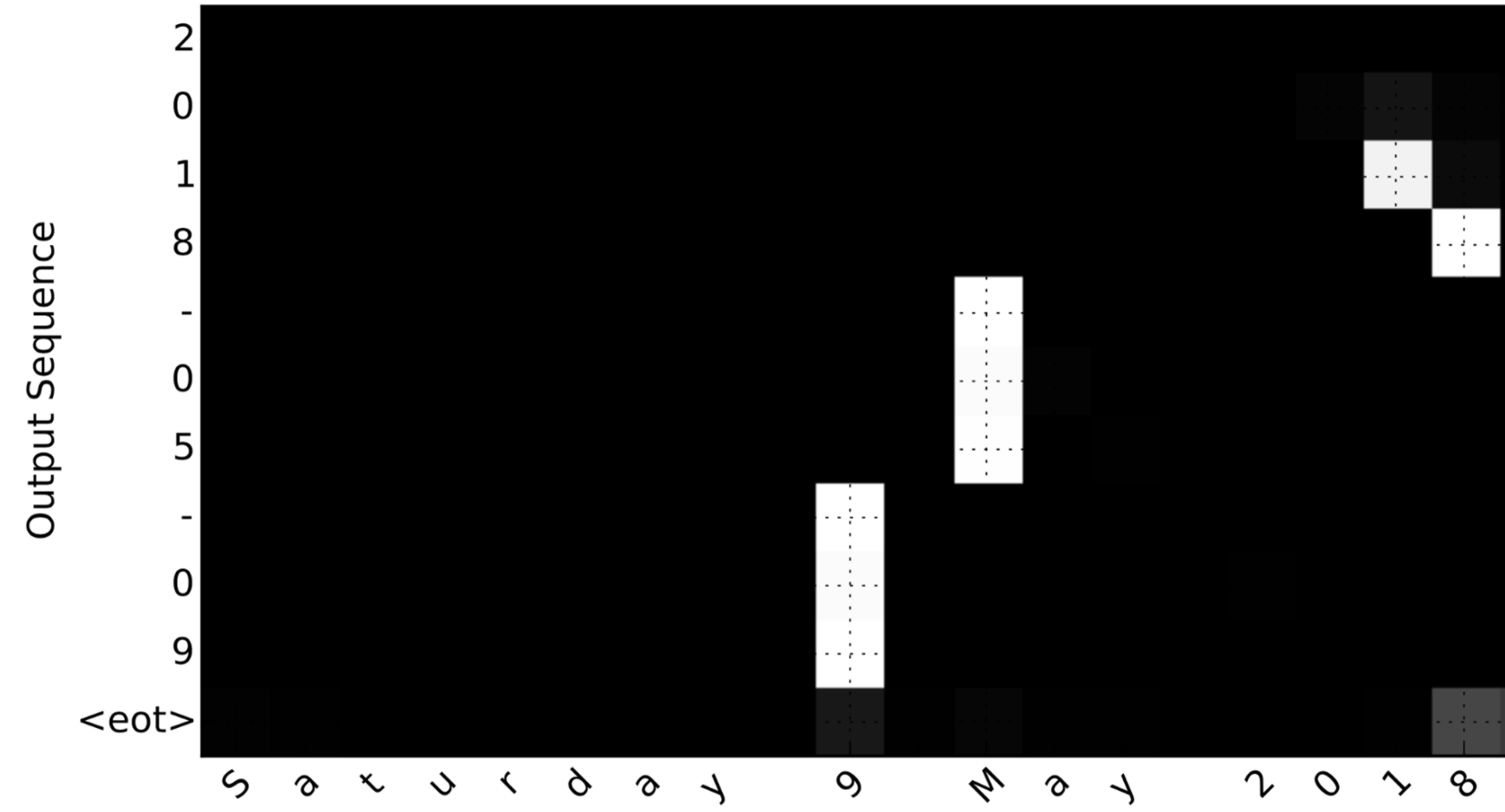
**Figure 8**: Full Attention Map
注意输出如何忽略输入的“星期六”部分,所有的输出时间步骤都没有注意到输入的这一部分。
我们还看到,9已经翻译成09,5月已经正确翻译成05,输出注意输入的部分,它需要进行翻译。 年份主要要求它注意输入的“18”以生成“2018”。
4.1 Getting the attention weights from the network
让我们现在可视化网络中的注意值。 我们将通过网络传播一个示例,然后可视化 \(\alpha^{\langle t, t' \rangle}\).
打印模型摘要:
model.summary()
network结构
____________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_6 (InputLayer) (None, 30, 37) 0
____________________________________________________________________________________________________
s0 (InputLayer) (None, 64) 0
____________________________________________________________________________________________________
bidirectional_6 (Bidirectional) (None, 30, 64) 17920 input_6[0][0]
____________________________________________________________________________________________________
repeat_vector_1 (RepeatVector) (None, 30, 64) 0 s0[0][0]
lstm_9[0][0]
lstm_9[1][0]
lstm_9[2][0]
lstm_9[3][0]
lstm_9[4][0]
lstm_9[5][0]
lstm_9[6][0]
lstm_9[7][0]
lstm_9[8][0]
____________________________________________________________________________________________________
concatenate_1 (Concatenate) (None, 30, 128) 0 bidirectional_6[0][0]
repeat_vector_1[14][0]
bidirectional_6[0][0]
repeat_vector_1[15][0]
bidirectional_6[0][0]
repeat_vector_1[16][0]
bidirectional_6[0][0]
repeat_vector_1[17][0]
bidirectional_6[0][0]
repeat_vector_1[18][0]
bidirectional_6[0][0]
repeat_vector_1[19][0]
bidirectional_6[0][0]
repeat_vector_1[20][0]
bidirectional_6[0][0]
repeat_vector_1[21][0]
bidirectional_6[0][0]
repeat_vector_1[22][0]
bidirectional_6[0][0]
repeat_vector_1[23][0]
____________________________________________________________________________________________________
dense_1 (Dense) (None, 30, 10) 1290 concatenate_1[14][0]
concatenate_1[15][0]
concatenate_1[16][0]
concatenate_1[17][0]
concatenate_1[18][0]
concatenate_1[19][0]
concatenate_1[20][0]
concatenate_1[21][0]
concatenate_1[22][0]
concatenate_1[23][0]
____________________________________________________________________________________________________
dense_2 (Dense) (None, 30, 1) 11 dense_1[13][0]
dense_1[14][0]
dense_1[15][0]
dense_1[16][0]
dense_1[17][0]
dense_1[18][0]
dense_1[19][0]
dense_1[20][0]
dense_1[21][0]
dense_1[22][0]
____________________________________________________________________________________________________
attention_weights (Activation) (None, 30, 1) 0 dense_2[13][0]
dense_2[14][0]
dense_2[15][0]
dense_2[16][0]
dense_2[17][0]
dense_2[18][0]
dense_2[19][0]
dense_2[20][0]
dense_2[21][0]
dense_2[22][0]
____________________________________________________________________________________________________
dot_1 (Dot) (None, 1, 64) 0 attention_weights[13][0]
bidirectional_6[0][0]
attention_weights[14][0]
bidirectional_6[0][0]
attention_weights[15][0]
bidirectional_6[0][0]
attention_weights[16][0]
bidirectional_6[0][0]
attention_weights[17][0]
bidirectional_6[0][0]
attention_weights[18][0]
bidirectional_6[0][0]
attention_weights[19][0]
bidirectional_6[0][0]
attention_weights[20][0]
bidirectional_6[0][0]
attention_weights[21][0]
bidirectional_6[0][0]
attention_weights[22][0]
bidirectional_6[0][0]
____________________________________________________________________________________________________
c0 (InputLayer) (None, 64) 0
____________________________________________________________________________________________________
lstm_9 (LSTM) [(None, 64), (None, 6 33024 dot_1[13][0]
s0[0][0]
c0[0][0]
dot_1[14][0]
lstm_9[0][0]
lstm_9[0][2]
dot_1[15][0]
lstm_9[1][0]
lstm_9[1][2]
dot_1[16][0]
lstm_9[2][0]
lstm_9[2][2]
dot_1[17][0]
lstm_9[3][0]
lstm_9[3][2]
dot_1[18][0]
lstm_9[4][0]
lstm_9[4][2]
dot_1[19][0]
lstm_9[5][0]
lstm_9[5][2]
dot_1[20][0]
lstm_9[6][0]
lstm_9[6][2]
dot_1[21][0]
lstm_9[7][0]
lstm_9[7][2]
dot_1[22][0]
lstm_9[8][0]
lstm_9[8][2]
____________________________________________________________________________________________________
dense_6 (Dense) (None, 11) 715 lstm_9[0][0]
lstm_9[1][0]
lstm_9[2][0]
lstm_9[3][0]
lstm_9[4][0]
lstm_9[5][0]
lstm_9[6][0]
lstm_9[7][0]
lstm_9[8][0]
lstm_9[9][0]
====================================================================================================
Total params: 52,960
Trainable params: 52,960
Non-trainable params: 0
浏览上面 model.summary() 的输出。
你可以看到图层名为 attention_weights 的输出 alphas 维度 (m, 30, 1) 在 dot_2 计算每个时间步 \(t=0,...,T_y - 1\)的上下文向量之前。
函数 attention_map() 从模型中提取注意值并绘制它们。
attention_map = plot_attention_map(model, human_vocab, inv_machine_vocab, "Tuesday 09 Oct 1993", num = 7, n_s = 64);
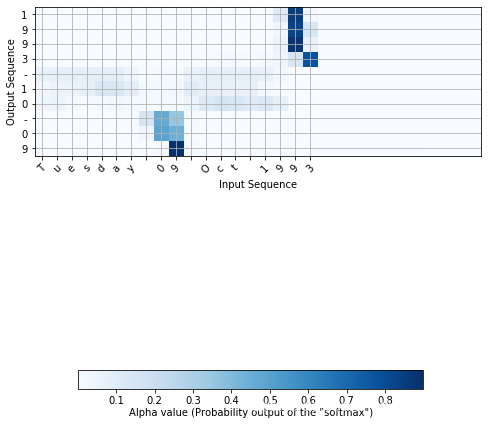
5. 完整代码
view code
#-*- coding: utf8 -*-
from keras.layers import Bidirectional, Concatenate, Permute, Dot, Input, LSTM, Multiply
from keras.layers import RepeatVector, Dense, Activation, Lambda
from keras.optimizers import Adam
from keras.utils import to_categorical
from keras.models import load_model, Model
import keras.backend as K
import numpy as np
from faker import Faker
import random
from tqdm import tqdm
from babel.dates import format_date
from nmt_utils import *
import matplotlib.pyplot as plt
m = 10000
dataset, human_vocab, machine_vocab, inv_machine_vocab = load_dataset(m)
print(dataset[:10])
print(human_vocab, len(human_vocab))
print(machine_vocab, len(machine_vocab))
Tx = 30
Ty = 10
X, Y, Xoh, Yoh = preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty)
print("X.shape:", X.shape)
print("Y.shape:", Y.shape)
print("Xoh.shape:", Xoh.shape)
print("Yoh.shape:", Yoh.shape)
index = 0
print("Source date:", dataset[index][0])
print("Target date:", dataset[index][1])
print()
print("Source after preprocessing (indices):", X[index])
print("Target after preprocessing (indices):", Y[index])
print()
print("Source after preprocessing (one-hot):", Xoh[index]) # 每行是一个T_t的输出,输出的是对应相应字符的一个one-hot向量.
print("Target after preprocessing (one-hot):", Yoh[index])
# Defined shared layers as global variables
repeator = RepeatVector(Tx)
concatenator = Concatenate(axis=-1)
densor1 = Dense(10, activation = "tanh")
densor2 = Dense(1, activation = "relu")
activator = Activation(softmax, name='attention_weights') # We are using a custom softmax(axis = 1) loaded in this notebook
dotor = Dot(axes = 1)
# GRADED FUNCTION: one_step_attention
def one_step_attention(a, s_prev):
"""
Performs one step of attention: Outputs a context vector computed as a dot product of the attention weights
"alphas" and the hidden states "a" of the Bi-LSTM.
Arguments:
a -- hidden state output of the Bi-LSTM, numpy-array of shape (m, Tx, 2*n_a)
s_prev -- previous hidden state of the (post-attention) LSTM, numpy-array of shape (m, n_s)
Returns:
context -- context vector, input of the next (post-attention) LSTM cell
"""
### START CODE HERE ###
# Use repeator to repeat s_prev to be of shape (m, Tx, n_s) so that you can concatenate it with all hidden states "a" (≈ 1 line)
s_prev = repeator(s_prev)
# Use concatenator to concatenate a and s_prev on the last axis (≈ 1 line)
# For grading purposes, please list 'a' first and 's_prev' second, in this order.
concat = concatenator([a, s_prev])
# Use densor1 to propagate concat through a small fully-connected neural network to compute the "intermediate energies" variable e. (≈1 lines)
e = densor1(concat)
# Use densor2 to propagate e through a small fully-connected neural network to compute the "energies" variable energies. (≈1 lines)
energies = densor2(e)
# Use "activator" on "energies" to compute the attention weights "alphas" (≈ 1 line)
alphas = activator(energies)
# Use dotor together with "alphas" and "a" to compute the context vector to be given to the next (post-attention) LSTM-cell (≈ 1 line)
context = dotor([alphas, a])
### END CODE HERE ###
return context
n_a = 32 # number of units for the pre-attention, bi-directional LSTM's hidden state 'a'
n_s = 64 # number of units for the post-attention LSTM's hidden state "s"
# Please note, this is the post attention LSTM cell.
# For the purposes of passing the automatic grader
# please do not modify this global variable. This will be corrected once the automatic grader is also updated.
post_activation_LSTM_cell = LSTM(n_s, return_state = True) # post-attention LSTM
output_layer = Dense(len(machine_vocab), activation=softmax)
# GRADED FUNCTION: model
def model(Tx, Ty, n_a, n_s, human_vocab_size, machine_vocab_size):
"""
Arguments:
Tx -- length of the input sequence
Ty -- length of the output sequence
n_a -- hidden state size of the Bi-LSTM
n_s -- hidden state size of the post-attention LSTM
human_vocab_size -- size of the python dictionary "human_vocab"
machine_vocab_size -- size of the python dictionary "machine_vocab"
Returns:
model -- Keras model instance
"""
# Define the inputs of your model with a shape (Tx,)
# Define s0 and c0, initial hidden state for the decoder LSTM of shape (n_s,)
X = Input(shape=(Tx, human_vocab_size))
s0 = Input(shape=(n_s,), name='s0')
c0 = Input(shape=(n_s,), name='c0')
s = s0
c = c0
# Initialize empty list of outputs
outputs = []
### START CODE HERE ###
# Step 1: Define your pre-attention Bi-LSTM. Remember to use return_sequences=True. (≈ 1 line)
a = Bidirectional(LSTM(n_a,return_sequences=True))(X)
# Step 2: Iterate for Ty steps
for t in range(Ty):
# Step 2.A: Perform one step of the attention mechanism to get back the context vector at step t (≈ 1 line)
context = one_step_attention(a, s)
# Step 2.B: Apply the post-attention LSTM cell to the "context" vector.
# Don't forget to pass: initial_state = [hidden state, cell state] (≈ 1 line)
s, _, c = post_activation_LSTM_cell(context, initial_state=[s, c])
# Step 2.C: Apply Dense layer to the hidden state output of the post-attention LSTM (≈ 1 line)
out = output_layer(s)
# Step 2.D: Append "out" to the "outputs" list (≈ 1 line)
outputs.append(out)
# Step 3: Create model instance taking three inputs and returning the list of outputs. (≈ 1 line)
model = Model([X, s0, c0], outputs)
### END CODE HERE ###
return model
model = model(Tx, Ty, n_a, n_s, len(human_vocab), len(machine_vocab))
model.summary()
### START CODE HERE ### (≈2 lines)
opt = Adam(lr = 0.005, beta_1=0.9, beta_2=0.999, decay=0.01)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
### END CODE HERE ###
s0 = np.zeros((m, n_s))
c0 = np.zeros((m, n_s))
outputs = list(Yoh.swapaxes(0,1))
model.fit([Xoh, s0, c0], outputs, epochs=1, batch_size=100)
model.load_weights('models/model.h5')
EXAMPLES = ['3 May 1979', '5 April 09', '21th of August 2016', 'Tue 10 Jul 2007', 'Saturday May 9 2018', 'March 3 2001', 'March 3rd 2001', '1 March 2001']
for example in EXAMPLES:
source = string_to_int(example, Tx, human_vocab)
source = np.array(list(map(lambda x: to_categorical(x, num_classes=len(human_vocab)), source))).swapaxes(0,1)
prediction = model.predict([source, s0, c0])
prediction = np.argmax(prediction, axis = -1)
output = [inv_machine_vocab[int(i)] for i in prediction]
print("source:", example)
print("output:", ''.join(output),"\n")
model.summary()
attention_map = plot_attention_map(model, human_vocab, inv_machine_vocab, "Tuesday 09 Oct 1993", num = 7, n_s = 64)
Sequence Model-week3编程题1-Neural Machine Translation with Attention的更多相关文章
- 课程五(Sequence Models),第三周(Sequence models & Attention mechanism) —— 1.Programming assignments:Neural Machine Translation with Attention
Neural Machine Translation Welcome to your first programming assignment for this week! You will buil ...
- Sequence Models Week 3 Neural Machine Translation
Neural Machine Translation Welcome to your first programming assignment for this week! You will buil ...
- 【转载 | 翻译】Visualizing A Neural Machine Translation Model(神经机器翻译模型NMT的可视化)
转载并翻译Jay Alammar的一篇博文:Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models Wi ...
- 对Neural Machine Translation by Jointly Learning to Align and Translate论文的详解
读论文 Neural Machine Translation by Jointly Learning to Align and Translate 这个论文是在NLP中第一个使用attention机制 ...
- On Using Very Large Target Vocabulary for Neural Machine Translation Candidate Sampling Sampled Softmax
[softmax分类器的加速器] https://www.tensorflow.org/api_docs/python/tf/nn/sampled_softmax_loss This is a fas ...
- 神经机器翻译 - NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE
论文:NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE 综述 背景及问题 背景: 翻译: 翻译模型学习条件分布 ...
- Effective Approaches to Attention-based Neural Machine Translation(Global和Local attention)
这篇论文主要是提出了Global attention 和 Local attention 这个论文有一个译文,不过我没细看 Effective Approaches to Attention-base ...
- [笔记] encoder-decoder NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE
原文地址 :[1409.0473] Neural Machine Translation by Jointly Learning to Align and Translate (arxiv.org) ...
- 改善深层神经网络-week3编程题(Tensorflow 实现手势识别 )
TensorFlow Tutorial Initialize variables Start your own session Train algorithms Implement a Neural ...
随机推荐
- Mysql常用sql语句(4)- distinct 去重数据
测试必备的Mysql常用sql语句系列 https://www.cnblogs.com/poloyy/category/1683347.html 前言 我们使用select进行数据查询时是会返回所有匹 ...
- Spring中使用@within与@target的一些区别
目录 背景 模拟项目例子 看看使用@within和@target的区别 @within @target @target 看起来跟合理一点 通知方法中注解参数的值为什么是不一样的 想用@within,但 ...
- idea鼠标双击.log日志文件无法打开
发现只要再mybatis-config.xml的起别名中加<package name="xxx"/>,就会导致Reader entry: ���� 1 n乱码,而R ...
- P1118 [USACO06FEB]Backward Digit Sums G/S
P1118 [USACO06FEB]Backward Digit Sums G/S 题解: (1)暴力法.对1-N这N个数做从小到大的全排列,对每个全排列进行三角形的计算,判断是否等于N. 对每个 ...
- 洛谷P1208——P1208 [USACO1.3]Mixing Milk(贪心)
题目描述 由于乳制品产业利润很低,所以降低原材料(牛奶)价格就变得十分重要.帮助Marry乳业找到最优的牛奶采购方案. Marry乳业从一些奶农手中采购牛奶,并且每一位奶农为乳制品加工企业提供的价格是 ...
- ubuntu安装git并配置SSH Key
安装git apt-get install git 配置git的用户名和邮箱: ssh-keygen -trsa -C "youremail@example.com" ssh-ke ...
- 测试验收标准checklist
需求实现功能清单 功能实现目的 需求改造功能清单 关联功能清单 关联系统 端到端全流程场景 业务联系性场景 业务全流程场景 上下需求关联规则 业务角度在流程中关注项 财报.评级 授信方案 反洗钱 面向 ...
- 通过JMETER后置处理器JSON Path Extractor插件来获取响应结果
学生金币充值接口:该接口有权限验证,需要admin用户才可以做操作,需要添加cookie.cookie中key为登录的用户名,value从登录接口中获取,登陆成功之后会返回sign. 通常做法是在HT ...
- docker run 参数
一.格式 docker run [OPTIONS] IMAGE [COMMAND] [ARG...] 二.OPTIONS 参数 简写, 名称参数 默认参数 描述 --add-host 添加自定义主机到 ...
- 使用three.js实现炫酷的酸性风格3D页面
背景 近期学习了 WebGL 和 Three.js 的一些基础知识,于是想结合最近流行的酸性设计风格,装饰一下个人主页,同时总结一些学到的知识.本文内容主要介绍,通过使用 React + three. ...
