Tikz绘制形似万花尺的图片

初中时意外发现数学课本上有这么一个好玩的图

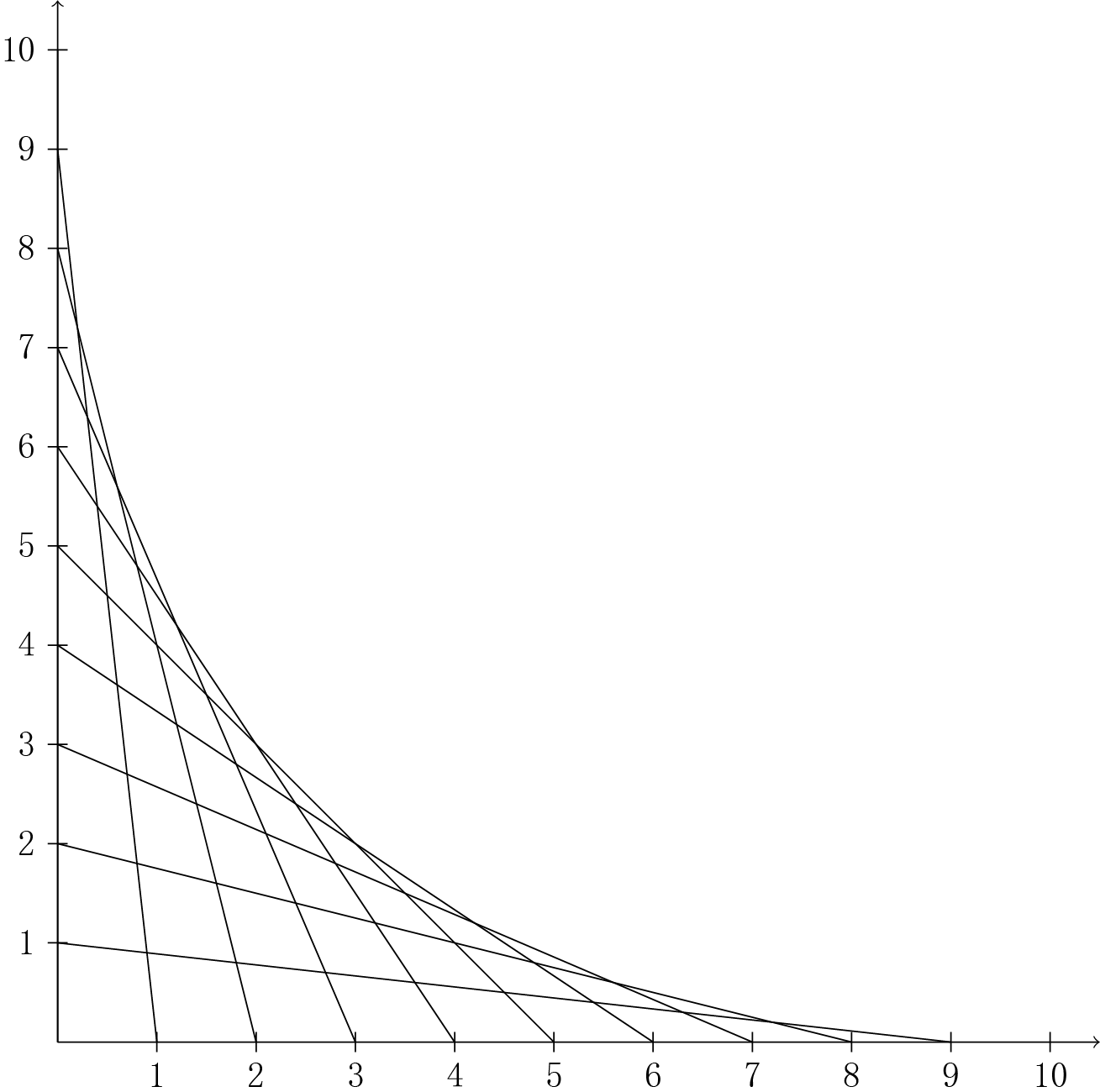
大概就是把两条相等线段A、B分为10个小段并在点上标序号，A线段1点连B线段9点，2点连8点，依次类推。

假设有这么一个框架图

按照第一张图的方式进一步绘图

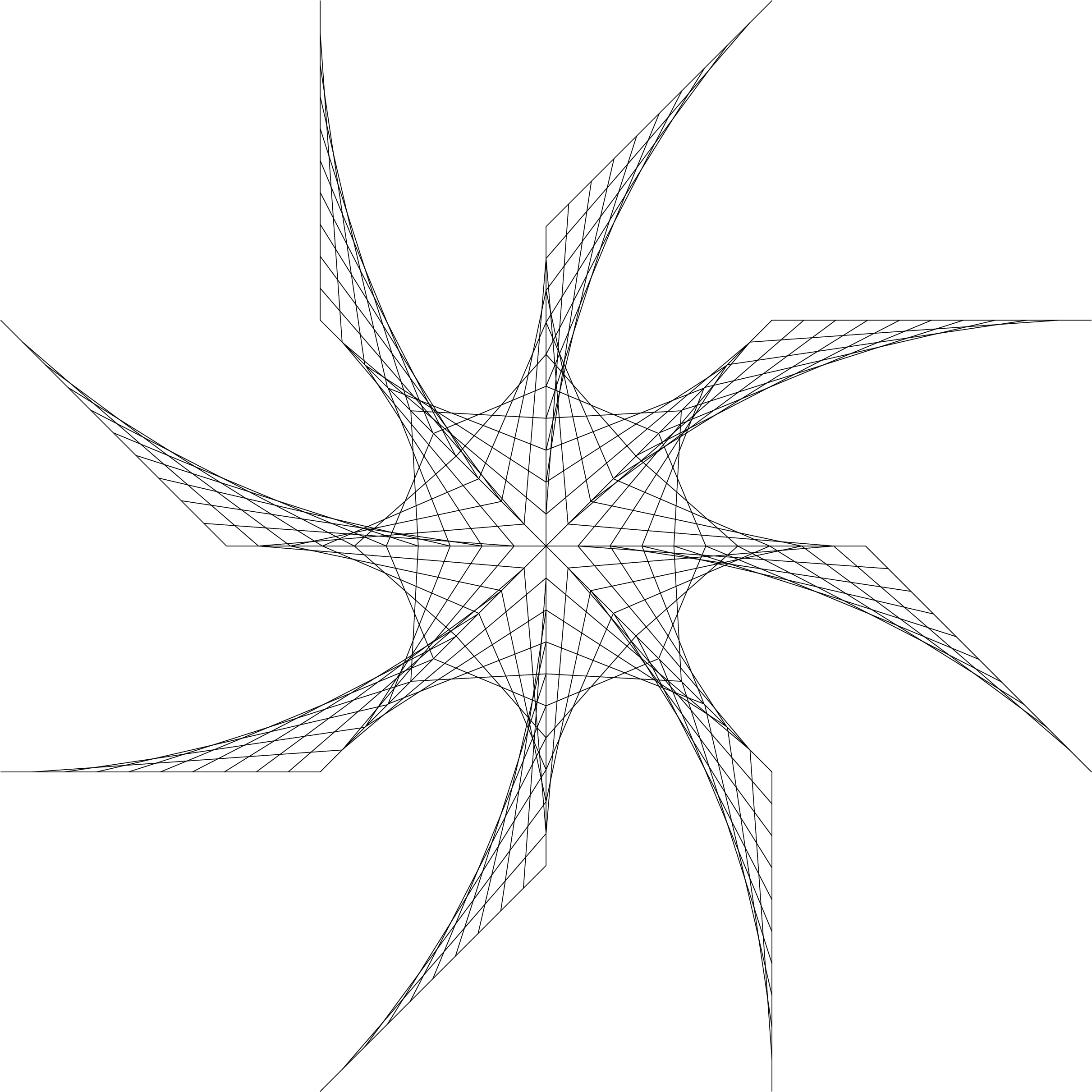
完整的tex文件代码如下：

\documentclass{article}
\usepackage{tikz}
\usepackage{geometry}
\pagestyle{empty}
\geometry{a4paper,left = 0.1cm, right = 0.1cm, top = 4cm, bottom = 2.5cm}
\begin{document}
%----------------框架----------------
\begin{center}
\begin{tikzpicture}
\draw[->](0,0)--(10.5,0);%坐标横线
\draw[->](0,0)--(0,10.5);%坐标纵线
\foreach\x in{1,...,10}
{
\draw(\x ,0.1cm)--(\x ,-0.1cm)node[anchor=north] {$\x$};%anchor表示方位
\draw(0.1cm,\x)--(-0.1cm,\x)node[anchor=east] {$\x$};%anchor表示方位
\draw(0,\x)--(10-\x,0);
}

\end{tikzpicture}
\end{center}\par
%----------------万花图框架----------------
\begin{center}
\begin{tikzpicture}[scale=0.6]
\draw(-10,0)--(10,0);%坐标横线
\draw(0,-10)--(0,10);%坐标纵线
\draw(-7.07,-7.07)--(7.07,7.07);%正斜
\draw(7.07,-7.07)--(-7.07,7.07);%反斜
%外圈框架
\draw(0,10)--(7.07,10+7.07);
\draw(7.07,7.07)--(10+7.07,7.07);
\draw(10,0)--(10+7.07,-7.07);
\draw(7.07,-7.07)--(7.07,-10-7.07);
\draw(0,-10)--(-7.07,-10-7.07);
\draw(-7.07,-7.07)--(-10-7.07,-7.07);
\draw(-10,0)--(-10-7.07,7.07);
\draw(-7.07,7.07)--(-7.07,7.07+10);

\end{tikzpicture}
\end{center}\par
%----------------万花图----------------
\begin{center}
\begin{tikzpicture}[scale=0.6]
\draw(-10,0)--(10,0);%坐标横线
\draw(0,-10)--(0,10);%坐标纵线
\draw(-7.07,-7.07)--(7.07,7.07);%正斜
\draw(7.07,-7.07)--(-7.07,7.07);%反斜
%外圈框架
\draw(0,10)--(7.07,10+7.07);
\draw(7.07,7.07)--(10+7.07,7.07);
\draw(10,0)--(10+7.07,-7.07);
\draw(7.07,-7.07)--(7.07,-10-7.07);
\draw(0,-10)--(-7.07,-10-7.07);
\draw(-7.07,-7.07)--(-10-7.07,-7.07);
\draw(-10,0)--(-10-7.07,7.07);
\draw(-7.07,7.07)--(-7.07,7.07+10);
\foreach\x in{1,...,9}
{
    %内圈
    \draw(0,\x)--(7.07-\x/1.41,7.07-\x/1.41);
    \draw(\x,0)--(7.07-\x/1.41,7.07-\x/1.41);
    \draw(0,-\x)--(7.07-\x/1.41,-7.07+\x/1.41);
    \draw(\x,0)--(7.07-\x/1.41,-7.07+\x/1.41);
    \draw(0,-\x)--(-7.07+\x/1.41,-7.07+\x/1.41);
    \draw(-\x,0)--(-7.07+\x/1.41,-7.07+\x/1.41);
    \draw(0,\x)--(-7.07+\x/1.41,7.07-\x/1.41);
    \draw(-\x,0)--(-7.07+\x/1.41,7.07-\x/1.41);
    %外圈
    \draw(0,\x)--(\x/1.41,10+\x/1.41);
    \draw(\x/1.41,\x/1.41)--(7.07+\x,7.07);
    \draw(\x,0)--(10+\x/1.41,-\x/1.41);
    \draw(\x/1.41,-\x/1.41)--(7.07,-7.07-\x);
    \draw(0,-\x)--(-\x/1.41,-10-\x/1.41);
    \draw(-\x/1.41,-\x/1.41)--(-7.07-\x,-7.07);
    \draw(-\x,0)--(-10-\x/1.41,\x/1.41);
    \draw(-\x/1.41,\x/1.41)--(-7.07,7.07+\x);
}
\end{tikzpicture}
\end{center}\par
\end{document}