CF1458D Flip and Reverse[题解]

Flip and Reverse

题目大意

给定一个 \(01\) 字符串，有机会进行若干次操作，对于每一次操作：

• 选择该字符串的子串，要求是该子串内包含数量相同的 \(0\) , \(1\) 字符。

• 将该子串内的所有字符取反， \(1\) 变成 \(0\) ，\(0\) 变成 \(1\) 。

• 把选中的子串顺序反转。

求经过若干次操作后字典序最小的字符串。

分析

若将 \(1\) 赋值为 \(1\) ， \(0\) 赋值为 \(-1\) ，进行前缀和运算，我们能够发现该操作的含义在前缀和中就是选择前缀和相同的两个点，将这两个点之间的前缀和反转。

例如样例 \(100101\) ，前缀和为 \(0\) , \(1\) , \(0\) , \(-1\) , \(0\) , \(-1\) , \(0\) 。

若我们选择前四个字符 \(1001\) 操作，等价于将七个前缀和中第 \(1\) 到第 \(5\) 个前缀和顺序反转，最后得到的结果都会是 \(011001\)。

通过前缀和图像我们能够较为轻松的发现这个性质：

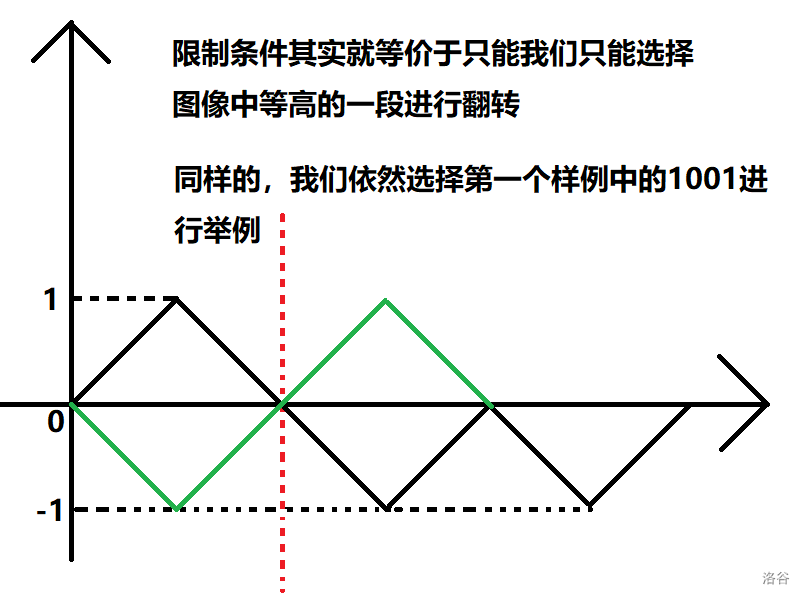
红色的线表示对称轴，绿色的线便是操作之后的前缀和，略作分析能够发现其正确性。

考虑如何求得答案，考虑贪心。我们没有必要一位一位的去操作，我们只需要考虑每一位的前缀和最小能够填几就可以了。简单的，如果目前位数的前缀和为 \(k\) ，那么下一位的前缀和有两种可能 \(k+1\) ， \(k-1\) ，我们当然想填 \(k-1\) ，考虑填入 \(k-1\) 的限制条件。

考虑对于原前缀和序列，每个数向相邻的数连无向边。由于对于前缀和序列的操作是选择子串翻转，并且开头和结尾的前缀和是一样的，那么其实不难发现，不管怎么操作，两个前缀和之间边的数量是不变的。

这样连边之后，能够填入 \(k-1\) 的有两种，第一种是没有连接 \(k+1\) 的边了，那么肯定就能够走 \(k-1\) ，第二种是 \(k\) 和 \(k-1\) 的连边至少有两条。

接下来说明为什么 \(k\) 和 \(k-1\) 的连边为什么至少需要两条。

• 如果 \(k\) 和 \(k-1\) 的连边只有一条，如果 \(k\) 后面直接就跟 \(k-1\) ，那么这种情况是肯定可以填的，但是由于我们已经知道了 \(k-1\) 和 \(k\) 的连边只有一条，所以最后不管怎么变化，前缀和不可能再回到 \(k\) ，自然也不会存在 \(k\) 与 \(k+1\) 的连边，则其实第一种情况就已经特判掉了只有一条连边时的情况。

• 那么 \(k\) 和 \(k-1\) 的连边有两条为什么一定对呢？首先后面原本就是 \(k-1\) 的情况当然是可以的，但是如果后面是 \(k+1\) ，要满足至少有两条与 \(k-1\)的连边，则必须满足如下图的前缀和变化：而排除掉第一种特殊情况，若只有一条连边的情况则如下图：

发现限制条件后，就可以贪心的往下填，最后求出的答案即是最优解。

CODE

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n;
char s[N];
int a[N],pre[N];
//edge[0/1][0/1][i]中第一位表示增减连边，第二位表示目前数值i的正负
int edge[2][2][N];
inline int read()
{
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
	return s*w;
}
int main()
{
	n=read();
	while(n--){
		scanf("\n%s",s+1);
		int len=strlen(s+1);
		for(register int i=1;i<=len;i++) a[i]=s[i]-'0';
		for(register int i=1;i<=len;i++){ //处理前缀和
			if(a[i]==1) pre[i]=pre[i-1]+1;
			else pre[i]=pre[i-1]-1;
		}
		for(register int i=0;i<len;i++){ //处理出前缀和与边的数量f
			int sym1= pre[i]>=0 ? 1 : 0,sym2= pre[i+1]>=0 ? 1 : 0;
			int change= pre[i+1]>pre[i] ? 1 : 0;
			edge[change][sym1][abs(pre[i])]++,edge[change^1][sym2][abs(pre[i+1])]++;
		}
		int now=0;
		for(register int i=1;i<=len;i++){ //考虑每一位如何填充
			int sym1= now>=0 ? 1 : 0;
			if(edge[0][sym1][abs(now)]>=2||!edge[1][sym1][abs(now)]){
				printf("0"),now--;
				int sym2= now>=0 ? 1 : 0;
				edge[0][sym1][abs(now+1)]--,edge[1][sym2][abs(now)]--;
			}
			else{
				printf("1"),now++;
				int sym2= now>=0 ? 1 : 0;
				edge[1][sym1][abs(now-1)]--,edge[0][sym2][abs(now)]--;
			}
		}
		printf("\n");
	}
	return 0;
}