OO第一单元总结——求导

一.基于度量分析程序结构

(一）第一次作业

（1）设计思路

本次作业只涉及到简单幂函数通过加减运算而复合而成的函数，因此笔者自然的把函数分成了函数本体以及单个的项两个部分，在笔者的设计中两个类的功能如下：

Poly：存储函数本体、将函数的各个项分解出来

Item：存储单个的项、单个项的求导、输出

（2）UML类图

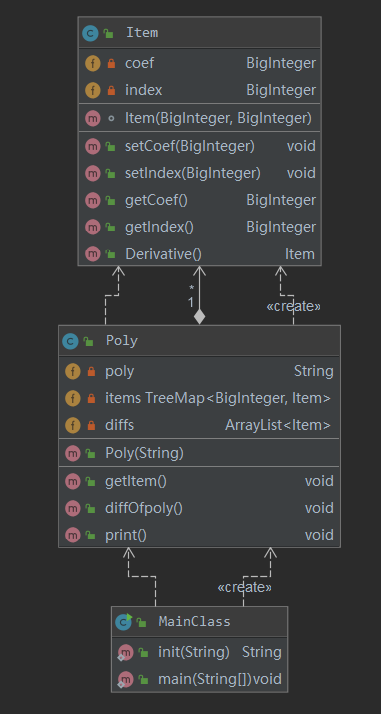
本次设计主要的采用了Poly和Item两个类，分别代表函数表达式和单个的幂函数因子，本次设计中存在的问题在于，主类中包含不必要的方法init()用以对字符串进行预处理，通过研讨课，笔者意识到在主类中只应该暴露给出用户直接使用的方法以确保程序的安全性，比如在该系列作业中，主类只需要调用求导方法即可。

（3）复杂度分析

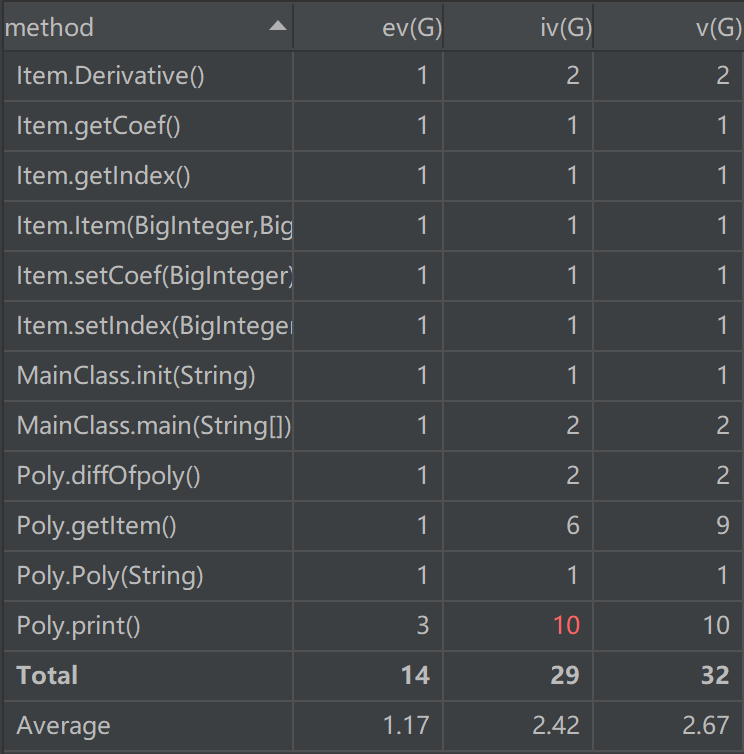
从复杂度看出此次作业中，poly.print()方法的iv(G)被标红，设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。由于在进行第一次作业时笔者还未认识到通过重写toString()方法可以实现直接通过调用System.out.println()进行输出，因此在此次作业中花费了大量的条件语句笨拙的实现了字符串的输出。

（4）bug分析

此次作业笔者未出现bug。

(二）第二次作业

（1）思路分析

相比第一次作业，第二次作业新增了三角函数以及乘法的复合形式。针对第二次作业新增的要求，笔者将单个的项看作的形式，将乘积形式复合的求导转化到单个项的求导中（事实证明这并不是一个好的方法，暂且按下不表）。类的设计与第一次大同小异，不再重复叙述。

（2）UML类图

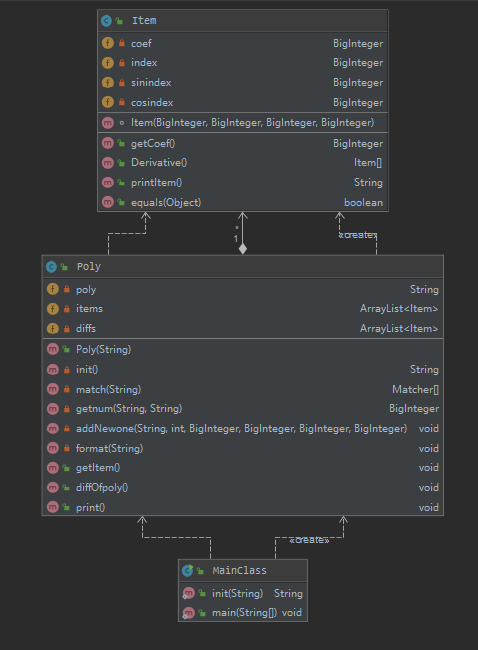
此次作业相比第一次作业，主类做到了简洁，只调用了必要的方法。但是Poly类中包含了高达9个方法，也就是说大部分的工作都是由Poly类完成的，该类即承担了存储的功能还承担了对表达式的各种复杂处理的功能，功能过于臃肿。

（3）复杂度分析

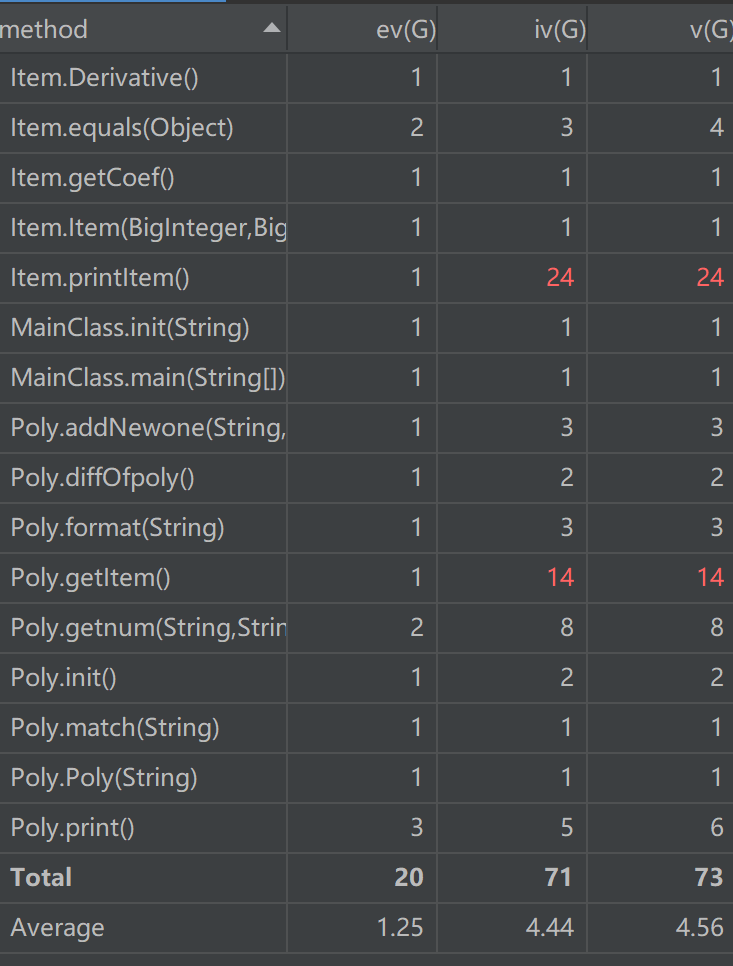
Item.printItem()和Poly.getItem()又被标红，前者的原因与第一次作业相同，为了简化输出做了很多的特判；后者的原因是该方法独立的承担了从项中分离出指数、因数等必要数据并完成存储的功能，笔者认为该方法的功能十分独立，为了完成功能的要求牺牲了复杂度是可以接受的。

（4）bug分析

本次作业笔者出现了bug，原因是对指导书的内容理解有误。具体如下：指导书规定指数的绝对值不超过10000，但是笔者误以为是化简结果的指数，比如x**10000*x**1，实际是正确的表达式，但是在化简后的结果为x**10001,于是被笔者的程序判定为WRONG FORMAT。这次bug也提醒笔者，对指导书的内容要充分理解，避免出错。

（三）第三次作业

（1）思路分析

第三次作业增加了嵌套规则，待函数复杂度瞬间大幅提升，导致在第二次作业的基础上几乎无法进行功能上的添加（这就是前文中提到的四元组不是好的方法的原因），于是在代码上几乎进行了重组，类的数量也大幅增加。在表达式的处理上采取了树形结构，建立表达式树以后从根节点开始向下求导。各个类的简介如下：

Sin , Cos , Exp , Const：构成函数的最简单的因子。

Add , Mul , Nest：加法、乘法、嵌套三种规则

Split：对表达式进行处理的函数类

Format：格式判断的函数类

（2）UML类图

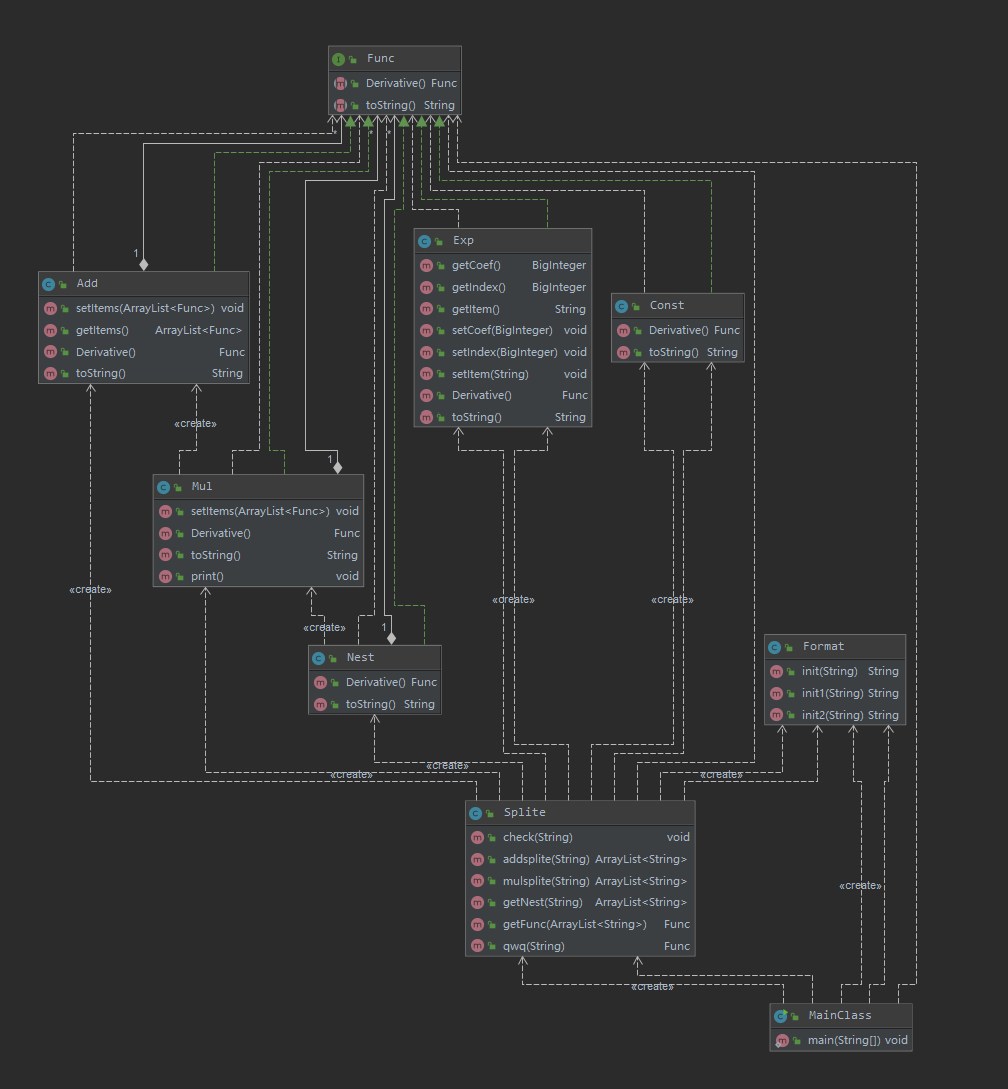
本次作业的主要功能的完成集中与Split类中，即数据分离，其他类的功能都比较简单。

和函数类都实现了Func接口，使得在求导过程中充分利用了多态的特性，笔者也认为这是本次作业中对笔者帮助最大的特性。

（3）复杂度分析

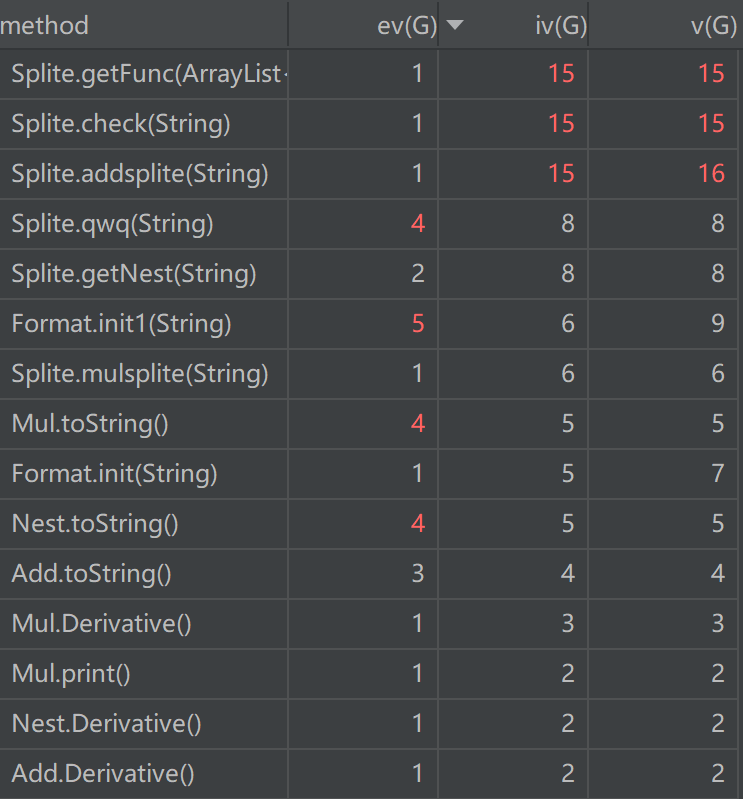
由于方法比较多，笔者只截取了标红的方法。在第三次作业中，笔者终于学会了重写toString()方法，在输出上的复杂度终于大幅下降。主要分析一下前三个方法，getFunc()方法是分离最基本因子（Exp,Sin,Cos,Const），check()方法是用于判断嵌套因子是否合法，addsplite()方法是分离表达式中通过加减相连的各项，这三个方法在构建表达式树的时候被频繁调用，因此iv(G)十分的高，这里我认为有很大的改进空间。

（4）bug分析

由于笔者的本次作业无效，因此没有参加强测和互测。于是笔者分析一下程序无效的原因。在乘法法则的求导规则是：(f(x)g(x))' = f(x)'g(x) + f(x)g(x)'，由于笔者在建立表达式树的时候只保存了求导后的结构，为保存原函数，于是笔者的乘法法则变为了：(f(x)g(x))' = f(x)'g(x) + f(x)'g(x)'，已经求过导的项在表达式中只会出现其导数的形式，导致了错误的发生。

二.探测bug策略

step1:在对自己的程序进行测试时，保存的样例。这部分主要是对程序的功能性的覆盖，但是一般很难通过这里找出bug。

step2:构造边界数据、特殊数据等，在本次作业中主要是指数的范围、特殊的指数（0、1、-1）、大量重复数据（如：x*x*x*x*x*x*x*x-x+x-x+x)；这些数据有可能找出bug。

step3:阅读代码，重点关注个人认为容易出错的地方，比如字符串的预处理和分离以及输出。

三.应用对象创建模式进行重构

三次作业笔者都是遵循，函数-表达项-因子的结构创建对象，但是对象的创建过程往往集中于函数类中，导致函数类中大量的实例化表达项类、因子类，使得函数类具有较高的复杂度。在对比优秀代码后，我发现在此次作业中工厂模式是十分有效的对象创建模式，在之后的设计中也应该多加注意对设计模式的应用。

四.心得和体会

（1）不足：1.关于三次作业中拓展性的考虑不够，进行了多次重构。现在回过头来思考三次作业，笔者认为其实就对应这相加、相乘、嵌套三个复合规则。如果在一开始就注意到这一点，在迭代开发的过程中依次实现相关的复合规则求导必然可以减少不必要的重构，同时也更加符合逻辑。

2.类的功能不清晰，在设计过程中出现了一个类中包含很多的方法，承担了过于多的功能的情况。在之后的设计中，如何抽象出类以及类的方法设计需要投入更加多的思考。

3.方法设置不合理，在设计过程中经常出现checkstyle时提醒方法过长，为了通过checkstyle而强行将一个方法进行拆分的情况。笔者认为一个方法的行数限制在60行是为了限制方法的复杂度，减少出错，同时从笔者阅读代码的实际情况来看，如果一个方法过长的话，阅读体验也会直线下降。刚开始笔者也在质疑一个方法限制60行是否合理，但是经过三次作业的实践我也认同了方法长度的限制。

4.与优秀代码进行对比之后，我发现优秀代码的共同特点是对功能的拆分做的十分细致和自然，一个类的长度往往不会很长。而笔者的代码就会出现1个类包含5个以上的方法的情况。除此，优秀代码往往也采用了合理的设计模式，比如工厂模式。在笔者的代码中基本上都是一种随性的生成模式，缺少优秀的设计模式，这是笔者亟待加强的部分。

（2)体会：首先，作为一个Java小白，通过pre系列的作业，笔者对Java有了初步的了解，但是笔者发现仅仅掌握初步的入门知识往往不足够，笔者认为对java语法的了解和设计思想的深入是相辅相成的，比如：java具有的多态特性使得我们可以通过工厂模式实例化不同的类，而在使用这些对象的相同方法时而不担心我们是否调用了正确的方法。其次，对面向对象的设计思想的理解和运用，目前笔者对对象的抽象仅停留在直观的层面，这是需要多加思考和交流的。最后，对时间的把控，在最后一次作业中，由于周五才开始进行，导致在最后测试时发现了设计上的重大错误，但是时间不足以支持修改完成的情况致使作业无效，这一点令笔者十分懊悔。通过总结我得出的几点经验是：尽早开始动手！尽早开始动手！尽早开始动手！；开始之前对程序的结构进行充分的思考，不要一边写一边思考（笔者的经验是这样很有可能造成写的到一半发现有问题又进行大规模的重写）；多参与讨论区的讨论，在讨论区有很多优秀的思路，本次的作业中讨论区也帮了笔者很大的忙。