一维DFT

学习DIP第3天

傅里叶变换是一个非常大的话题。今天实现了下一维的DFT，兴许将完毕其它傅里叶系的算法实现和实验。

DFT公式：

                       

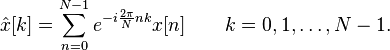
    当中e 是自然对数的底数，i是虚数单位。通常以符号表示这一变换，即

                 

IDFT公式：

                                 

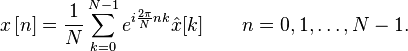
   记为：

                            

c语言代码：

//
//  main.c
//  Fourer1D
//
//  Created by Tony on 14/11/16.
//  Copyright (c) 2014年 Tony. All rights reserved.
//

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define SIZE 1000
#define VALUE_MAX 2000
struct Complex_{
    double real;
    double imagin;
};
typedef struct Complex_ Complex;

void setInput(double * data,int n){
    printf("Setinput signal:\n");
    srand((int)time(0));
    for(int i=0;i<SIZE;i++){
        data[i]=rand()%VALUE_MAX;
        printf("%lf\n",data[i]);
    }

}
void DFT(double * src,Complex * dst,int size){
    clock_t start,end;
    start=clock();

    for(int m=0;m<size;m++){
        double real=0.0;
        double imagin=0.0;
        for(int n=0;n<size;n++){
            double x=M_PI*2*m*n;
            real+=src[n]*cos(x/size);
            imagin+=src[n]*(-sin(x/size));

        }
        dst[m].imagin=imagin;
        dst[m].real=real;
        if(imagin>=0.0)
            printf("%lf+%lfj\n",real,imagin);
        else
            printf("%lf%lfj\n",real,imagin);
    }
    end=clock();
    printf("DFT use time :%lf for Datasize of:%d\n",(double)(end-start)/CLOCKS_PER_SEC,size);

}

void IDFT(Complex *src,Complex *dst,int size){
    //Complex temp[SIZE];
    clock_t start,end;
    start=clock();
    for(int m=0;m<size;m++){
        double real=0.0;
        double imagin=0.0;
        for(int n=0;n<size;n++){
            double x=M_PI*2*m*n/size;
            real+=src[n].real*cos(x)-src[n].imagin*sin(x);
            imagin+=src[n].real*sin(x)+src[n].imagin*cos(x);

        }
        real/=SIZE;
        imagin/=SIZE;
        if(dst!=NULL){
            dst[m].real=real;
            dst[m].imagin=imagin;
        }
        if(imagin>=0.0)
            printf("%lf+%lfj\n",real,imagin);
        else
            printf("%lf%lfj\n",real,imagin);
    }
    end=clock();
    printf("IDFT use time :%lfs for Datasize of:%d\n",(double)(end-start)/CLOCKS_PER_SEC,size);

}
int main(int argc, const char * argv[]) {
    double input[SIZE];
    Complex dst[SIZE];
    setInput(input,SIZE);
    printf("\n\n");
    DFT(input, dst, SIZE);
    printf("\n\n");
    IDFT(dst, NULL, SIZE);

}