学习笔记 | CDQ分治

目录

• 前言
• 啥是CDQ啊(它的基本思想)
• 例题
• 后记
• 参考博文

前言

博主太菜了 学习快一年的OI了 好像没有什么会的算法
更寒碜的是 学一样还不精一样TAT
如有什么错误请各位路过的大佬指出啊感谢!

啥是CDQ啊(它的基本思想)

• cdq 一个离线的算法
• 我们要解决一系列问题，这些问题一般包含修改和查询操作，可以把这些问题排成一个序列，用一个区间[L,R]表示。
• 分。递归处理左边区间[L,M]和右边区间[M+1,R]的问题。
• 治。合并两个子问题，同时考虑到[L,M]内的修改对[M+1,R]内的查询产生的影响。即，用左边的子问题帮助解决右边的子问题。

分而治之就叫分治妈呀我在讲啥
这就是CDQ分治的基本思想。和普通分治不同的地方在于，普通分治在合并两个子问题的过程中，[L,M]内的问题不会对[M+1,R]内的问题产生影响。
Q: 考虑一下归并排序为什么合并的时候 只用算左边对右边区间的贡献？
因为它一个区间里的贡献已经计算完了

例题

hdu5618Jam's problem again

啊一道三维偏序魔板题

题意:给出\(n\)个点的三维坐标\((x,y,z)\) 对每个点\(i\) 找到满足\(x_j \leq x_i,y_j \leq y_i,z_j \leq z_i\)的\(j\)的数量

可以先把\(x\)这一维排序排掉 那么之后算答案的时候就不用考虑\(x\)的影响 再用类似于归并排序的算法 将\(y\)从小到大排序
那么合并左右两个区间的时候 右边区间的\(x\)必定大于左边区间的\(x\) 且在每个区间里的\(y\)都是单调递增的
那么\(y\)用two_pointer扫一下 , \(z\)用树状数组去维护

tps:

• 每次当然不能暴力memset清空树状数组 可以考虑倒回去清空（也就是用了多少清空多少
• 当两个点相等时 肯定只是把这个点的答案算到了一个点上 那么如何判断有没有算过呢 cdq结束之后排在\(i\)前面的点对\(i\)的贡献一定全算上了 但在\(i\)后面的点没有算上
  所以最后再计算一下漏掉的就可以了

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10;
struct data{
    int id;
    int x,y,z;
}a[N],c[N];
int tr[N],d[N],g[N];

int lowerbit(int x){ return x&(-x); }

void UPD(int x,int y){
    for(;x<N;x+=lowerbit(x)) tr[x]+=y;
}

void Qk(int x){
    for(;x<N;x+=lowerbit(x)) tr[x]=0;
}

int Get(int x){
    int ans=0;
    for(;x;x-=lowerbit(x)) ans+=tr[x];
    return ans;
}

bool cmp(data xx,data yy){
    if(xx.x!=yy.x) return xx.x<yy.x;
    if(xx.y!=yy.y) return xx.y<yy.y;
    if(xx.z!=yy.z) return xx.z<yy.z;
}

bool check(data xx,data yy){
    return xx.y<=yy.y;
}

void CDQ(int l,int r){
    if(l==r) return ;
    int mid=(l+r)>>1;
    CDQ(l,mid),CDQ(mid+1,r);
    int lt=l-1,nw=l;
    fr(i,mid+1,r){
        int flg=0;
        fr(j,lt+1,mid){
            if(!check(a[j],a[i])){
                flg=1;
                lt=j-1;
                break;
            } else {
                UPD(a[j].z,1);
                c[nw++]=a[j];
            }
        }
        if(!flg) lt=mid;
        d[a[i].id]+=Get(a[i].z);
        c[nw++]=a[i];
    }
    fr(i,lt+1,mid) c[nw++]=a[i];
    fr(i,l,lt) Qk(a[i].z);
    fr(i,l,r) {
        a[i]=c[i];
    }
}

int main(){
    int T;scanf("%d",&T);
    fr(o,1,T){
        memset(d,0,sizeof d);
        int n;scanf("%d",&n);
        fr(i,1,n) scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z),a[i].id=i;
        sort(a+1,a+1+n,cmp);
        CDQ(1,n);
        int lt=1;
        rf(i,n-1,1){
            if(a[i].x!=a[i+1].x||a[i].y!=a[i+1].y||a[i].z!=a[i+1].z){
                lt=1;
            } else lt++;
            d[a[i].id]+=lt-1;
        }
        fr(i,1,n) printf("%d\n",d[i]);
    }
    return 0;
}

hdu4742Pinball Game 3D

题意:给出\(n\)个点的三维坐标\((x,y,z)\) 随意排序 最长不下降的子序列长度是多少 在满足这样的条件下方案数有多少个?
并且给出的点不会重复

对每个点再维护一个\(dp\)值和方案数 大的点肯定是从小的点转移过来的 所以这里分治的顺序需要考虑一下
先递归左区间 再用左区间的值更新右区间 最后再递归右区间

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10,mod=1073741824;
struct data{
    int x,y,z,id;
}a[N],b[N];
struct node{
    int dp;
    LL f;
}tr[N],d[N];
LL tot=0;
int Ax[N],Ay[N],Az[N];
int n,ans=0;

void read(int &x){
    char ch=getchar();x=0;
    for(;ch<'0'||ch>'9';ch=getchar());
    for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
}

void Add(LL &x,LL y){
    x=(x+y)%mod;
}

bool cmp(data xx,data yy){
    if(xx.x!=yy.x) return xx.x<yy.x;
    if(xx.y!=yy.y) return xx.y<yy.y;
    if(xx.z!=yy.z) return xx.z<yy.z;
}

bool cmpy(data xx,data yy){
    if(xx.y!=yy.y) return xx.y<yy.y;
    else return xx.z<yy.z;
}

void Go(node &x,node y){
    if(x.dp<y.dp) x.dp=y.dp,x.f=y.f;
    else if(x.dp==y.dp) Add(x.f,y.f);
}

void Ch(int x){
    if(d[x].dp<ans) return ;
    else if(d[x].dp==ans) Add(tot,d[x].f);
    else ans=d[x].dp,tot=d[x].f;
}

int lowerbit(int x){ return x&(-x); }

void Upd(int x,node y){
    for(;x<N;x+=lowerbit(x)) Go(tr[x],y);
}

node Get(int x){
    if(!x) return (node){0,0};
    node tmp;tmp.dp=0,tmp.f=0;
    for(;x;x-=lowerbit(x)) Go(tmp,tr[x]);
    return tmp;
}

void Qk(int x){
    for(;x<N;x+=lowerbit(x)) tr[x].dp=0,tr[x].f=0;
}

void cdq(int l,int r){
    if(l==r) return ;
    int mid=(l+r)>>1;
    cdq(l,mid);
    sort(a+l,a+1+mid,cmpy);
    sort(a+mid+1,a+1+r,cmpy);
    int pos=l-1,nw=l;
    fr(i,mid+1,r){
        while(pos+1<=mid&&a[pos+1].y<=a[i].y){
            pos++,Upd(a[pos].z,(node){d[a[pos].id].dp,d[a[pos].id].f});
        }
        node gg=Get(a[i].z);
        gg.dp++;
        Go(d[a[i].id],gg);
    }
    fr(i,l,pos) Qk(a[i].z);
    sort(a+mid+1,a+1+r,cmp);
    cdq(mid+1,r);
}

int main(){
    int T;read(T);
    fr(o,1,T){
        read(n);
        ans=0,tot=0;
        fr(i,1,n) {
            scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z),a[i].z++,a[i].id=i;
            Ax[i]=a[i].x,Ay[i]=a[i].y,Az[i]=a[i].z;
        }
        sort(Ax+1,Ax+1+n),sort(Ay+1,Ay+1+n),sort(Az+1,Az+1+n);
        Ax[0]=unique(Ax+1,Ax+1+n)-Ax-1;
        Ay[0]=unique(Ay+1,Ay+1+n)-Ay-1;
        Az[0]=unique(Az+1,Az+1+n)-Az-1;
        fr(i,1,n){
            a[i].x=lower_bound(Ax+1,Ax+1+Ax[0],a[i].x)-Ax;
            a[i].y=lower_bound(Ay+1,Ay+1+Ay[0],a[i].y)-Ay;
            a[i].z=lower_bound(Az+1,Az+1+Az[0],a[i].z)-Az;
        }
        fr(i,1,n) d[i].dp=1,d[i].f=1;
        sort(a+1,a+1+n,cmp);
        cdq(1,n);
        fr(i,1,n) Ch(i);
        printf("%d %lld\n",ans,tot);
        fr(i,1,n) d[i]=(node){0,0LL};
    }
    return 0;
}

hdu4456Crowd

给出一张\(n*n\)的坐标系 有两个操作

1. 给\((x,y)\)的权值加上\(c\)
   2.询问与\((x,y)\)的曼哈顿距离\(\leq k\)的点的点权和
   \(n \leq 1e4,m \leq 8e4\)

坐标旋转 二维数点 CDQ

可以观察到 与一个点曼哈顿距离小于等于某个数所构成的图形是每个角都为90°的菱形

可以考虑点旋转或坐标轴旋转 避免根号 不妨将边长扩大为原来的\(\sqrt{2}\)倍
cdq时套上二维数点即可

tps: 二维数点

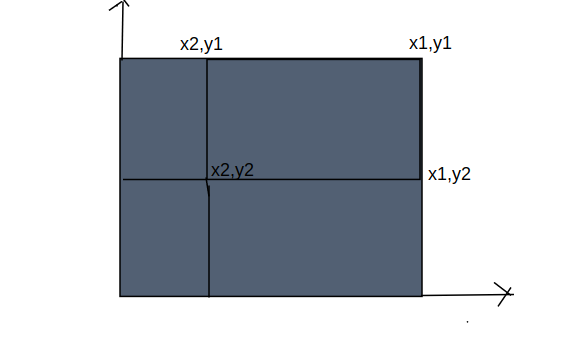
如果要求\((x1,y1,x2,y2)\)的价值 是不是相当于\(w_(x1,y1,0,0)-w_(x1,y2-1,0,0)-w_(x2-1,y1,0,0)+w_(x2-1,y2-1,0,0)\)
那么对于每个询问 先对时间排序 再对\(x\)排序 最后\(y\)所对应的值用树状数组去维护怎么套路和三位偏序一模一样!!

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=4e6+10,M=8e4+10,WF=3e4+10;
struct data{
    int tp,x,y,v,rk,flg;
}q[N],b[N];
int ans[M],tr[N];
int n,m;

int lowerbit(int x){ return x&(-x); }

void Upd(int x,int y){
    for(;x<N;x+=lowerbit(x)) tr[x]+=y;
}

int Get(int x){
    int ans=0;
    for(;x;x-=lowerbit(x)) ans+=tr[x];
    return ans;
}

void cdq(int l,int r){
    if(l==r) return ;
    int mid=(l+r)>>1;
    cdq(l,mid),cdq(mid+1,r);
    int pos=l-1,nw=l;
    //printf("l=%d r=%d\n",l,r);
    fr(i,mid+1,r){
        while(pos+1<=mid&&q[pos+1].x<=q[i].x){
            pos++;b[nw++]=q[pos];
            if(q[pos].tp==1) {
      //          cout<<q[pos].y<<" zz"<<q[pos].v<<endl;
                Upd(q[pos].y,q[pos].v);
            }
        }
        if(q[i].tp==2) {
            ans[q[i].rk]+=q[i].flg*Get(q[i].y);
      //      cout<<q[i].rk<<" ??"<<ans[q[i].rk]<<endl;
        }
        b[nw++]=q[i];
    }
    fr(i,pos+1,mid) b[nw++]=q[i];
    fr(i,l,pos) if(q[i].tp==1) Upd(q[i].y,-q[i].v);
    fr(i,l,r) {
        q[i]=b[i];
       // printf("tp=%d x=%d y=%d v=%d flg=%d rk=%d\n",q[i].tp,q[i].x,q[i].y,q[i].v,q[i].flg,q[i].rk);
    }
}

int main(){
    while(scanf("%d",&n)==1&&n){
        scanf("%d",&m);
        int cnt=0,tot=0;
        fr(i,1,m){
            int tp,x,y,v;
            scanf("%d%d%d%d",&tp,&x,&y,&v);
            if(tp==1) q[++tot].tp=tp,q[tot].x=x+y+WF,q[tot].y=x-y+WF,q[tot].v=v;
            else {
                int nx=x+y+WF,ny=x-y+WF;++cnt;
                q[++tot].tp=tp,q[tot].x=nx-v-1,q[tot].y=ny+v,q[tot].rk=cnt,q[tot].flg=-1;
                q[++tot].tp=tp,q[tot].x=nx+v,q[tot].y=ny-v-1,q[tot].rk=cnt,q[tot].flg=-1;
                q[++tot].tp=tp,q[tot].x=nx+v,q[tot].y=ny+v,q[tot].rk=cnt,q[tot].flg=1;
                q[++tot].tp=tp,q[tot].x=nx-v-1,q[tot].y=ny-v-1,q[tot].rk=cnt,q[tot].flg=1;
            }
        }
       /* fr(i,1,tot){
            printf("tp=%d x=%d y=%d v=%d flg=%d rk=%d\n",q[i].tp,q[i].x,q[i].y,q[i].v,q[i].flg,q[i].rk);
        }*/
        cdq(1,tot);
        //TAT
        fr(i,1,cnt) printf("%d\n",ans[i]);
        fr(i,1,cnt) ans[i]=0;
      //  puts("WTF!\n");
    }
    return 0;
}

CQOI2011动态逆序对 1A真是开心~

本题是删除一个数之后 求出所有逆序对的数量
发现正着做好像很难啊啊w(ﾟДﾟ)w
"遇难则反"
所以倒过来 我们考虑插入
那么是不是是需要考虑每次插入一个数 所增加的逆序对数是多少?
这样我们就很容易转换成了三位偏序问题
第一维是时间 第二维是位置 第三维是值
套个魔板就珂以啦QwQ

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10;
struct data{
    int x,y,z;
}qx[N],gg[N];
int n,m;
int ys[N],vis[N],a[N];
LL tr[N],ans[N];

void read(int &x){
    char ch=getchar();x=0;
    for(;ch<'0'||ch>'9';ch=getchar()) ;
    for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
}

int lowerbit(int x){ return x&(-x); }

LL Get(int x){
    LL ans=0;
    if(!x) return 0LL;
    for(;x;x-=lowerbit(x)) ans+=tr[x];
    return ans;
}

void Upd(int x,int k){
    for(;x<N;x+=lowerbit(x)) tr[x]+=k;
}

void Qk(int x){
    for(;x<N;x+=lowerbit(x)) tr[x]=0;
}

void cdq(int l,int r){
    int mid=(l+r)>>1;
    if(l==r) return ;
    cdq(l,mid),cdq(mid+1,r);
    int pos=l-1,nw=l;
    //printf("l=%d r=%d\n",l,r);
    fr(i,mid+1,r){
        while(pos+1<=mid&&qx[pos+1].y<qx[i].y){
            pos++,gg[nw++]=qx[pos],Upd(qx[pos].z,1);
        }
        gg[nw++]=qx[i];
        ans[qx[i].x]+=(pos-l+1)-Get(qx[i].z-1);
    }
    fr(i,pos+1,mid) gg[nw++]=qx[i];
    fr(i,l,pos) Qk(qx[i].z);
    pos=mid+1;
    rf(i,r,mid+1){
        while(pos-1>=l&&qx[pos-1].y>qx[i].y){
            pos--,Upd(qx[pos].z,1);
        }
        ans[qx[i].x]+=Get(qx[i].z-1);
    }
    fr(i,pos,mid) Qk(qx[i].z);
    fr(i,l,r) qx[i]=gg[i];
}

int main(){
    read(n),read(m);
    fr(i,1,n) scanf("%d",&a[i]),ys[a[i]]=i;
    int cz=n+1;
    fr(i,1,m){
        int x;scanf("%d",&x);
        vis[x]=1;
        qx[--cz].y=ys[x],qx[cz].z=x,qx[cz].x=cz;
    }
    fr(i,1,n) if(!vis[i]) qx[--cz].y=ys[i],qx[cz].z=i,qx[cz].x=cz;
    cdq(1,n);
    /*fr(i,1,n){
        printf("mdans=%lld\n",ans[i]);
    }*/
    fr(i,1,n) ans[i]+=ans[i-1];
    rf(i,n,n-m+1) printf("%lld\n",ans[i]);
    return 0;
}

bzoj1492|NOI2007货币兑换

题意 还是看原题吧TAT

可以显然得出 每一天要么不操作要么全部卖出 要不全部买入
那么我们设\(dp[i]\)表示前\(i\)天的最大获利
\[dp[i]=dp[i-1]\]
\[dp[i]=max_{j=1}^{i-1}(\dfrac{dp[j]*R[j]}{R[j]*A[j]+B[j]}*A[i]+\dfrac{f[j]}{R[j]*A[j]+B[j]}*B[i])\]
我们把\(\dfrac{dp[j]*R[j]}{R[j]*A[j]+B[j]}\)记作\(x\) , \(\dfrac{f[j]}{R[j]*A[j]+B[j]}\)记作\(y\)
\[dp[i]=max_{j=1}^{i-1}(x*A[i]+y*B[i])\]
是不是可以斜率优化啊QwQ 但是这个斜率并不是单调的QwQ
这里介绍cdq分治 我不会splay啊TAT
左区间将\(x,y\)水平序排序 维护一个斜率递减的凸包
右区间将斜率\(\frac{-A[i]}{B[i]}\)排序
就可以啦
注意一下细节

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=(x);i<=(y);++i)
#define rf(i,x,y) for(int i=(x);i>=(y);--i)
#define LL long long
#define db double
using namespace std;
const int N=1e5+10;
const db eps=1e-10;
struct data{
    int id;
    db x,y,A,B,R,k;
}q[N];
int Q[N];
db dp[N];

bool comp(data xx,data yy){
    return xx.k<yy.k;
}

bool cmp(data xx,data yy){
    return xx.x<yy.x||(xx.x==yy.x&&xx.y<yy.y);
}

bool Cmp(data xx,data yy){
    return xx.id<yy.id;
}

db Cross(db xx,db xy,db yx,db yy){
    return xx*yy-xy*yx;
}

db js(int tp,int i){
    return q[Q[tp]].x*q[i].A+q[Q[tp]].y*q[i].B;
}

void cdq(int l,int r){
    if(l==r){
       // cout<<q[l].id<<"WAI"<<endl;
        dp[q[l].id]=max(dp[q[l].id],dp[q[l].id-1]);
        q[l].x=dp[q[l].id]/(q[l].R*q[l].A+q[l].B)*q[l].R;
        q[l].y=dp[q[l].id]/(q[l].R*q[l].A+q[l].B);
        return ;
    }
    int mid=(l+r)>>1;
    cdq(l,mid);
    sort(q+l,q+mid+1,cmp);
    sort(q+mid+1,q+r+1,comp);
    int tp=0;
    /*fr(i,mid+1,r){
        db maxn=0;int kk=-1;
        fr(j,l,mid) {
            if(maxn<q[j].x*q[i].A+q[j].y*q[i].B) kk=j;
            maxn=max(maxn,q[j].x*q[i].A+q[j].y*q[i].B);
        }
        dp[q[i].id]=max(dp[q[i].id],maxn);
        printf("gg%d %lf %d\n",q[i].id,dp[q[i].id],kk);
    }*/
    fr(i,l,mid){
        while(tp>=2&&Cross(q[i].x-q[Q[tp]].x,q[i].y-q[Q[tp]].y,q[i].x-q[Q[tp-1]].x,q[i].y-q[Q[tp-1]].y)<=0) tp--;
        Q[++tp]=i;
    }
    fr(i,mid+1,r){
        db pos=js(tp,i);
        while(js(tp-1,i)>pos) tp--,pos=js(tp,i);
        dp[q[i].id]=max(dp[q[i].id],pos);
    }
    sort(q+mid+1,q+r+1,Cmp);
    cdq(mid+1,r);
}

int main(){
    int n;
    scanf("%d%lf",&n,&dp[0]);
    fr(i,1,n){
        q[i].id=i;
        scanf("%lf%lf%lf",&q[i].A,&q[i].B,&q[i].R);
        q[i].k=-q[i].A/q[i].B;
    }
    cdq(1,n);
  //  fr(i,0,n) printf("%.3f\n",dp[i]);
    printf("%.3f\n",dp[n]);
    return 0;
}

/*
10 100
5.007 5.139 1.44
5.142 5.963 1.39
5.248 5.038 1.06
5.705 5.606 1.07
5.151 5.067 1.86
5.924 5.979 1.88
5.069 5.912 1.28
5.075 5.092 1.77
5.485 5.409 1.28
5.161 5.233 1.63
148.311
*/

bzoj4553序列

题意 给出一个数组\(a[]\)
有\(m\)个操作 每次操作修改\(a_x\)为\(y\) 操作之间不影响
问这个数组的最长子序列使得在每一次操作过后都是非递减的QwQ

由于每一次操作都只修改一个位置 所以 每个位置在所有操作中的最大\(mx_i\)和最小值\(mn_i\)我们都可以知道
对于\(i < j\) 若\(j\)能够接到\(i\)的后面
那么必须满足 \(mx[i] \leq a[j]\) && \(a[i] \leq mn[j]\)
对左区间按\(a\)排序 右区间按照\(mn\)排序
\(mx_j\)和\(a_i\)的关系用树状数组维护

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10;
int ans=0;
int b[N],dp[N],mx[N],mn[N],a[N],tr[N];

int lowerbit(int x){ return x&(-x); }

void Upd(int x,int y){
    for(;x<N;x+=lowerbit(x)) tr[x]=max(tr[x],y);
}

void Qk(int x){
    for(;x<N;x+=lowerbit(x)) tr[x]=0;
}

int Get(int x){
    int pos=0;
    for(;x;x-=lowerbit(x)) pos=max(pos,tr[x]);
    return pos;
}

bool cmp1(int x,int y){
    return a[x]<a[y];
}

bool cmp2(int x,int y){
    return mn[x]<mn[y];
}

bool cmp3(int x,int y){
    return x<y;
}

void cdq(int l,int r){
    if(l==r) return ;
    int mid=(l+r)>>1;
    cdq(l,mid);
    sort(b+l,b+mid+1,cmp1);
    sort(b+mid+1,b+r+1,cmp2);
    int pos=l-1;
    fr(i,mid+1,r){
        while(pos+1<=mid&&a[b[pos+1]]<=mn[b[i]]){
            pos++;
            Upd(mx[b[pos]],dp[b[pos]]);
        }
        dp[b[i]]=max(dp[b[i]],Get(a[b[i]])+1);
    }
    fr(i,l,pos) Qk(mx[b[i]]);
    sort(b+mid+1,b+r+1,cmp3);
    cdq(mid+1,r);
}

int main(){
    int n,m;scanf("%d%d",&n,&m);
    fr(i,1,n) scanf("%d",&a[i]),mx[i]=a[i],mn[i]=a[i];
    fr(i,1,m){
        int x,y;
        scanf("%d%d",&x,&y);
        mx[x]=max(mx[x],y);
        mn[x]=min(mn[x],y);
    }
    fr(i,1,n) b[i]=i,dp[i]=1;
    cdq(1,n);
    fr(i,1,n) ans=max(ans,dp[i]);
    printf("%d\n",ans);
    return 0;
}

后记

啊...cdq就学习到这里吧
根据517的指示 魔版题也差不多做了做
剩下的就随缘了

参考博文

__stdcall 【教程】简易CDQ分治教程&学习笔记