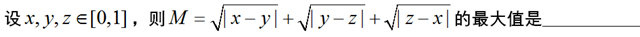
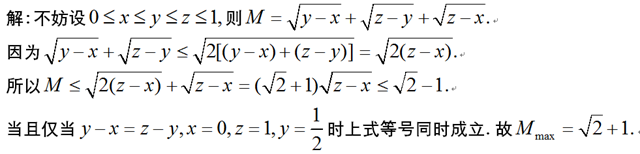
评：这是一道浙江省省赛题，这里利用对称性，设$x\le y\le z$从而解决了问题。值得注意的是此处三元轮换对称正好也是完全对称，但如果变成一般的$n\ge4$元对称问题时，就不能设大小关系。事实上有如下难题：

解答：

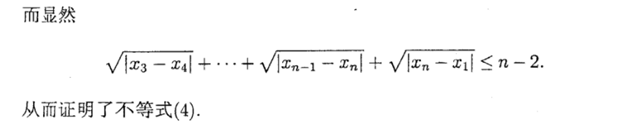
MT【98】三元对称不等式的更多相关文章

  1. 从首个IMO季军谈起 作者 : 付云皓

    刚刚过去的IMO,中国史无前例地获得了第三名,也是自1997年来近20年首次跌出前二.感谢微信等社交软件,相信现在这个新闻已经以火箭的速度传播了. 作为一个与数学竞赛及IMO打了多年交道的人,我一直有 ...

  2. MT【138】对称乎？

    已知\(a+b=1\),求\((a^3+1)(b^3+1)\)的最大值______ : 解答: \[ \begin{align*} (a^3+1)(b^3+1) &=a^3+b^3+a^3+b ...

  3. MT【25】切线不等式原理及例题

    评:切线不等式和琴生(Jesen)不等式都是有其几何意义的,在对称式中每一项单变量后利用图像的凹凸性得到一个线性的关系式.已知的条件往往就是线性条件,从而可以得到最值.

  4. MT【57】2017联赛一试解答倒数第二题:一道不等式的最值

    注:康拓诺维奇不等式的应用

  5. MT【33】证明琴生不等式

    解答:这里数学归纳法证明时指出关键的变形. 评:撇开琴生不等式自身的应用和意义外,单单就这个证明也是一道非常不错的练习数学归纳法的经典题目.

  6. MT【200】一道自招的不等式

    (2018武汉大学自招)设$x,y,z\ge0,xy+yz+zx=1$证明:$\dfrac{1}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{z+x}\ge \dfrac{5}{2}$ ...

  7. MT 【331】两元非齐次不等式

    若正实数$x,y$满足$x^3+y^3=(4x-5y)y$ 则 $y$ 的最大值为____ 解答:$x^3+y^3+y^2=4(x-y)y\le x^2$,故$y^3+y^2=x^2-x^3=\dfr ...

  8. MT【327】两道不等式题

    当$x,y\ge0,x+y=2$时求下面式子的最小值:1)$x+\sqrt{x^2-2x+y^2+1}$2)$\dfrac{1}{5}x+\sqrt{x^2-2x+y^2+1}$ 解:1)$P(x,y ...

  9. MT【322】绝对值不等式

    已知 $a,b,c\in\mathbb R$,求证:$|a|+|b|+|c|+|a+b+c|\geqslant |a+b|+|b+c|+|c+a|$ 分析:不妨设$c=\max\{a,b,c\},\d ...

随机推荐

  1. AI Summit（2018.07.19）

    AI Summit 时间:2018.07.19地点:北京丽都皇冠假日酒店

  2. 2017-2018-2 20155315《网络对抗技术》Exp6 ：信息搜集与漏洞扫描

    实验目的 进行信息搜集的工作,为实战做准备 教程 实验内容 外围信息搜集 NMAP OpenVAS 实验步骤 (一)各种搜索技巧的应用 实战的前提是进行信息搜索.当我们想要有针对地进行操作的时候,就要 ...

  3. Oracle中，如何查看FRA(Flashback Recovery Area)的利用率

    例子: SQL> set linesize 300SQL> select * from V$RECOVERY_AREA_USAGE; FILE_TYPE PERCENT_SPACE_USE ...

  4. 汇编 push ,pop指令

    知识点:  PUSH  POP  CALL堆栈平衡  RETN指令 一.PUSH入栈指令 (压栈指令): 格式: PUSH 操作数 //sub esp,4 ;mov [esp],EBP 操作数 ...

  5. python 回溯法 子集树模板 系列 —— 12、选排问题

    问题 从n个元素中挑选m个元素进行排列,每个元素最多可重复r次.其中m∈[2,n],r∈[1,m]. 如:从4个元素中挑选3个元素进行排列,每个元素最多可重复r次. 分析 解x的长度是固定的,为m. ...

  6. python 回溯法 子集树模板 系列 —— 6、排课问题

    问题 某乡村小学有六个年级,每个年级有一个班,共六个班. 周一到周五,每天上6节课,共计30节课. 开设的课程 一年级:语(9)数(9)书(2)体(2)美(2)音(2)德(2)班(1)安(1) 二年级 ...

  7. IOS免越狱虚拟定位修改工具共享 Jocation

    Jocation IOS虚拟定位修改器 具体使用方法可以按照 location cleaned软件相同的操作. 主要是因为本人有一部 IphoneX 和Iphone Xs Max 网上的locatio ...

  8. 爱普生L313彩色打印相片

    操作环境: windows 和MAC 一.普通打印(默认选项) 1.爱普生L313 普通默认打印为快速不清晰打印. 2.以上打印效果出来图片比较快速出图,但是清晰度不够 二.照片打印设置 1.照片设置 ...

  9. torchvision 批量可视化图片

    1.1 简介 计算机视觉中,我们需要观察我们的神经网络输出是否合理.因此就需要进行可视化的操作. orchvision是独立于pytorch的关于图像操作的一些方便工具库. torchvision的详 ...

  10. Unity 角色场景传送功能

    传送触发器 using System.Collections;using System.Collections.Generic;using UnityEngine;using UnityEngine. ...