PAT甲级——1123 Is It a Complete AVL Tree （完全AVL树的判断）

嫌排版乱的话可以移步我的CSDN：https://blog.csdn.net/weixin_44385565/article/details/89390802

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

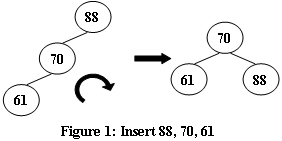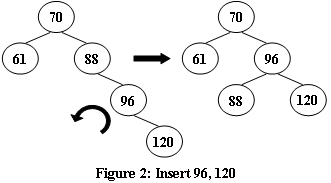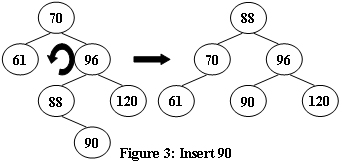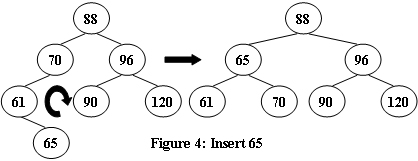Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.

Sample Input 1:

5
88 70 61 63 65

Sample Output 1:

70 63 88 61 65
YES

Sample Input 2:

8
88 70 61 96 120 90 65 68

Sample Output 2:

88 65 96 61 70 90 120 68
NO

题目大意：给出N个数据，建立AVL树，并判断其是否为完全二叉树。

思路：题目言简意赅，就两个核心操作：建立AVL树、判断是否为完全二叉树~~

AVL树的建立过程详见我之前的文章：AVL树（自平衡二叉查找树）

因为AVL树本身的性质已经保证了左右子树的高度差≤1，所以之后判断完全二叉树主要有两个条件：1、对于每个节点，左子树高度≥右子树高度；2、层序遍历遇到一个节点，它有左孩子但没有右孩子时标记一下，在它之后进入队列的节点都为叶子节点，这棵AVL树为完全二叉树。

 #include <iostream>
 #include <queue>
 #define ElementType int
 using namespace std;
 typedef struct node *AVLTree;
 struct node {
     ElementType key;
     int Height = ;
     AVLTree left = NULL, right = NULL;
 };
 bool flag = true;
 int Height(AVLTree tree);//求树的高度
 ElementType Max(ElementType a, ElementType b);
 AVLTree insert(AVLTree tree, ElementType &key);//在AVLTree中插入节点
 AVLTree LL_Rotation(AVLTree tree);//LL旋转
 AVLTree RR_Rotation(AVLTree tree);//RR旋转
 AVLTree LR_Rotation(AVLTree tree);//LR旋转
 AVLTree RL_Rotation(AVLTree tree);//RL旋转
 void levelTraversal(AVLTree tree);//层序遍历

 int main()
 {
     int N;
     ElementType key;
     AVLTree tree = NULL;
     scanf("%d", &N);
     for (int i = ; i < N; i++) {
         cin >> key;
         tree = insert(tree, key);
     }
     levelTraversal(tree);
     if (flag)
         printf("YES\n");
     else
         printf("NO\n");

 }

 AVLTree insert(AVLTree tree, ElementType &key) {
     if (tree == NULL) {
         tree = new node();
         tree->key = key;
     }
     else if (key < tree->key) {
         tree->left = insert(tree->left, key);//key小于当前节点的值时继续往其左子树递归地插入
         if (Height(tree->left) - Height(tree->right) >= ) {//左子树与右子树的高度差达到2的时候就要对当前节点进行旋转，这里由于是递归地执行，保证了平衡因子达到2的节点是最接近插入点的
             if (key < tree->left->key)
                 tree = LL_Rotation(tree);
             else
                 tree = LR_Rotation(tree);
         }
     }
     else {
         tree->right = insert(tree->right, key);
         if (Height(tree->right) - Height(tree->left) >= ) {
             if (key > tree->right->key)
                 tree = RR_Rotation(tree);
             else
                 tree = RL_Rotation(tree);
         }
     }
     tree->Height = Max(Height(tree->left), Height(tree->right)) + ;//当前节点的高度为其最大子树的高度+1
     return tree;
 }

 AVLTree LR_Rotation(AVLTree tree) {
     tree->left = RR_Rotation(tree->left);
     return LL_Rotation(tree);
 }

 AVLTree RL_Rotation(AVLTree tree) {
     tree->right = LL_Rotation(tree->right);
     return RR_Rotation(tree);
 }

 AVLTree RR_Rotation(AVLTree tree) {
     AVLTree tree2 = tree->right;
     tree->right = tree2->left;
     tree2->left = tree;
     tree->Height = Max(Height(tree->left), Height(tree->right)) + ;
     tree2->Height = Max(Height(tree2->right), tree->Height) + ;
     return tree2;
 }

 AVLTree LL_Rotation(AVLTree tree) {
     AVLTree tree2 = tree->left;
     tree->left = tree2->right;
     tree2->right = tree;
     tree->Height = Max(Height(tree->left), Height(tree->right)) + ;
     tree2->Height = Max(Height(tree->left), tree->Height) + ;
     return tree2;
 }

 int Height(AVLTree tree) {
     if (tree == NULL)
         return ;
     return tree->Height;
 }

 ElementType Max(ElementType a, ElementType b) {
     return a > b ? a : b;
 }

 void levelTraversal(AVLTree tree)
 {
     bool flag2 = false;
     AVLTree t = NULL;
     queue <AVLTree> Q;
     Q.push(tree);
     while (!Q.empty()) {
         t = Q.front();
         Q.pop();
         cout << t->key;
         if (flag2 && Height(t) != ) //高度为1的节点就是叶子节点
             flag = false;
         if (Height(t->left) < Height(t->right)) //AVL树保证了每个节点的左右子树高度差小于等于1，只要左子树高度小于右子树，这课AVL树就不是完全二叉树
             flag = false;
         if (t->left != NULL && t->right == NULL) //遇到一个节点，有左孩子但没有右孩子，标记一下，它之后的存入队列中的节点都为叶子节点时这棵AVL树才是完全二叉树
             flag2 = true;
         if (t->left != NULL)
             Q.push(t->left);
         if (t->right != NULL)
             Q.push(t->right);
         if (!Q.empty())
             printf(" ");
     }
     printf("\n");
 }