集训Day2

雅礼集训2017Day2

T1

给你一个水箱，水箱里有n-1个挡板，水遵循物理定律

给你m个条件，表示第i个格子上面y+1高度的地方有或没有水

现在给你无限的水从任意地方往下倒，问最多满足多少条件

n,m 1e5

SOL：

考虑答案的表示方法，肯定是类似于dp["区间1到n"]这种的

“区间1到n”这个东西我们可以状压，就过了20%

另外10%的数据只有“有水”的条件 我们cout<<m

另外30%的n平方做法肯定是要用到dp（我没有想出来这个东西怎么搞到n平方）

。。。

这里是全知全能的XiongGod提供的一种n平方做法

对于每一个条件，可以将其视为l到r区间的最高/最低高度为x；

把所有条件记录下来后就成了区间选择问题的版题，分成上下界两种讨论dp就好了

考虑暴力碾标算

一个区间能能不能“有水”取决于中间最长的那个木板

于是可以考虑递归建一棵“线段树”

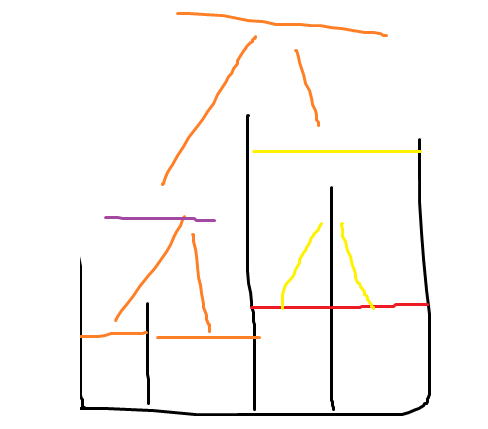
这样一个区间的问题就可以递归到左右儿子解决

且因为这是棵线段树，最多nlogn个点

然后树形DP

$d[i]$表示i节点水没有漫出去的情况

$f[i]$表示i节点水漫出去的情况

式子由于...这是要给学妹（实际只有学弟吧？）看的

所以你们自己推吧

T2

一个100*100的棋盘，有地方有障碍

Alice和Bob两个人玩游戏，Alice放一个棋子，Bob先手二人轮流移动棋子

要求：不能移到障碍上且走过的地方不能走

不能动就输了

求Alice的必胜点

SOL：

原题啊...

将棋盘黑白染色建出二分图 有障碍直接跳过就行了

考虑对于一个完美匹配，Bob（先手）按匹配边走就可以了

对于不完美的最大匹配，Alice可以把棋放在“不一定是最大匹配”的地方，让Bob走非匹配边，自己走匹配边

现在就是要考虑如何求这个“不一定是最大匹配”的点

跑完dinic，从S开始跑未满流的边，跑到左边的且非S的点就是“不一定是最大匹配”的

T开始跑未满流的边，跑到右边且非T的点就是“不一定是最大匹配的”

为什么正确可以通过交错路定理来证明一下

时间复杂度是O(您用的二分图匹配算法 + 棋盘大小)

100 + 100 + 0 = 200？

T3前30随便写可是没时间写了...

话说是不是上午时间不够啊

如果再给我半个小时就是100 + 100 + 30 = 230了（再次大众分

#include<bits/stdc++.h>
#define LL long long
inline int read() {
    int x = ,f = ;
    char ch = getchar();
    for(; !isdigit(ch); ch = getchar())if(ch == '-')f = -f;
    for(; isdigit(ch); x =  * x + ch - '',ch = getchar());
    return x * f;
}
const int maxn = 2e5 + ,inf = ;
int n,m,N;
int fa[maxn],bot[maxn],top[maxn],dx[maxn];
int ST[][maxn];
int son[maxn][];
int f[maxn],d[maxn];
 
struct block {
    int h,pos;
} hs[maxn];
bool cmp(const block &a,const block &b) {
    if(a.h == b.h)return a.pos < b.pos;
    return a.h < b.h;
}
struct info {
    int h,type;
    bool operator < (const info &a)const {
        if(h == a.h)return type < a.type;
        return h < a.h;
    }
};
 
std::vector<info> vec[maxn];
 
inline int find(int x) {
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}
 
int main() {
    int T = read();
    while(T--) {
        n = read(),m = read();
        N = n;
        memset(dx,,sizeof(dx));
        memset(fa,,sizeof(fa));
        memset(f,,sizeof(f));
        memset(d,,sizeof(d));
        int S,T,sum,sz,tmp;
        for(int i=; i<n; i++) {
            hs[i].h = read();
            hs[i].pos = i;
        }
        std::sort(hs + ,hs + n,cmp);
        bot[] = inf;
        for(int i=; i<=n; i++)top[i] = i,fa[i] = i;
        for(int i=; i<n; i++) {
            int fx = find(hs[i].pos),fy = find(hs[i].pos + );
            bot[++N] = hs[i].h;
            ST[][N] = ;
            ST[][top[fx]] = N;
            ST[][top[fy]] = N;
            son[N][] = top[fx],son[N][] = top[fy];
            fa[fy] = fx;
            top[fx] = N;
        }
        for(int i=; i<=N; i++)vec[i].clear();
        for(int i=; i<=; i++)
            for(int j=; j<=N; j++)
                ST[i][j]=ST[i-][ST[i-][j]];
        int x,y,k;
        for(int i=; i<=m; i++) {
            x = read(),y = read(),k = read();
            for(int j=; j>=; j--)
                if(bot[ST[j][x]] <= y)x = ST[j][x];
            vec[x].push_back((info) {y,k});
            dx[x] += !k;
        }
        for(int i=; i<=N; i++)std::sort(vec[i].begin(),vec[i].end());
        for(int i=; i<=N; i++) {
            if(!vec[i].empty()) {
                sz = vec[i].size();
                S = ;
                d[i] = sum = dx[i] + ( i > n ? f[son[i][]] + f[son[i][]] : );
                while(S < sz) {
                    T = S;
                    tmp = (vec[i][T].type ?  : -);
                    while(T +  < sz && vec[i][T+].h == vec[i][T].h)
                        ++T,tmp += (vec[i][T].type ?  : -);
                    sum += tmp;
                    d[i] = std::max(d[i],sum);
                    S = T + ;
                }
                f[i] = sum;
            }
            if(i > n) {
                d[i] = std::max(d[i],dx[i] + d[son[i][]] + d[son[i][]]);
                f[i] = std::max(f[i],f[son[i][]] + f[son[i][]]);
            }
        }
        printf("%d\n",d[N]);
    }
}

T1（压行太严重就用了Astyle）

#include<bits/stdc++.h>
using namespace std;
const int _MAX = ,MAX_POINT = ,MAXE = ,inf = ;
const int dx[] = {,,-,,};
const int dy[] = {,,,,-};
int ans[MAX_POINT];
int m,n;
int S = ,T = MAX_POINT - ;
char s[_MAX][_MAX];
int pos[_MAX][_MAX],col[MAX_POINT],vis[MAX_POINT];
struct DINIC
{
    int first[MAX_POINT],cnt;
    int next[MAXE],to[MAXE],caps[MAXE];
    int deep[MAX_POINT];
    DINIC(){cnt = ;}
    void add(int x,int y,int f)
    {
        next[++cnt] = first[x];
        to[cnt] = y;
        caps[cnt] = f;
        first[x] = cnt;
    }
    void insert(int x,int y,int f)
    {
        add(x,y,f);
        add(y,x,);
    }
    bool BFS()
    {
        queue<int> q;
        memset(deep,,sizeof(deep));
        deep[S] = ;
        q.push(S);
        while(!q.empty())
        {
            int x = q.front(); q.pop();
            for(int i = first[x]; i; i = next[i])
                if(caps[i] && !deep[to[i]])
                {
                    deep[to[i]] = deep[x] + ;
                    q.push(to[i]);
                    if(to[i] == T)    return true;
                }
        }
        return false;
    }
    int dfs(int x,int f)
    {
        if(x == T)    return f;
        int temp = f;
        for(int i = first[x]; i; i = next[i])
            if(caps[i] && deep[to[i]] == deep[x] +  && temp)
            {
                int w = dfs(to[i],min(caps[i],temp));
                if(!w) deep[to[i]] = ;
                caps[i] -= w;
                caps[i^] += w;
                temp -= w;
            }
        return f - temp;
    }
}G;
 
int ctt;
void DFS(int x,int f)
{
    vis[x] = ;
    if(col[x] == f && x != S && x != T)ans[++ctt] = x;
    for(int i = G.first[x]; i; i = G.next[i])
        if(G.caps[i] == f && !vis[G.to[i]])DFS(G.to[i],f);
}
void solveGraph()
{
    for(int i = ; i <= m; i++)
        for(int j = ; j <= n; j++)
        {
            if(s[i][j] == '#')    continue;
            if(!((i + j)&))G.insert(S,pos[i][j],),col[pos[i][j]] = ;
            else
            {
                G.insert(pos[i][j],T,);
                continue;
            }
            for(int k = ; k <= ; k++)
            {
                int fx = i + dx[k],fy = j + dy[k];
                if(fx <  || fy <  || fx > m || fy > n)    continue;
                if(s[fx][fy] == '.')G.insert(pos[i][j],pos[fx][fy],);
            }
        }
    while(G.BFS())G.dfs(S,inf);
    DFS(S,);memset(vis,,sizeof(vis));DFS(T,);
}
int main()
{
    scanf("%d%d",&m,&n);
    for(int i = ; i <= m; i++)
        scanf("%s",s[i] + );
    int cnt = ;
    for(int i = ; i <= m; i++)
        for(int j = ; j <= n; j++)
            pos[i][j] = ++cnt;
    solveGraph();
    printf("%d\n",ctt);
    sort(ans + ,ans + ctt + );
    for(int i = ; i <= ctt; i++)printf("%d %d\n",(ans[i] - ) / n + ,(ans[i] - ) % n + );
    return ;
}

T2