【点分治】luoguP2664 树上游戏

应该是一道中等难度的点分？麻烦在一些细节。

题目描述

lrb有一棵树，树的每个节点有个颜色。给一个长度为n的颜色序列，定义s(i,j) 为i 到j 的颜色数量。以及

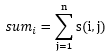
现在他想让你求出所有的sum[i]

输入输出格式

输入格式：

第一行为一个整数n，表示树节点的数量

第二行为n个整数，分别表示n个节点的颜色c[1],c[2]……c[n]

接下来n-1行，每行为两个整数x,y，表示x和y之间有一条边

输出格式：

输出n行，第i行为sum[i]

说明

sum[1]=s(1,1)+s(1,2)+s(1,3)+s(1,4)+s(1,5)=1+2+3+2+2=10
sum[2]=s(2,1)+s(2,2)+s(2,3)+s(2,4)+s(2,5)=2+1+2+1+3=9
sum[3]=s(3,1)+s(3,2)+s(3,3)+s(3,4)+s(3,5)=3+2+1+2+3=11
sum[4]=s(4,1)+s(4,2)+s(4,3)+s(4,4)+s(4,5)=2+1+2+1+3=9
sum[5]=s(5,1)+s(5,2)+s(5,3)+s(5,4)+s(5,5)=2+3+3+3+1=12

对于40%的数据，n<=2000

对于100%的数据，1<=n,c[i]<=10^5

---

题目分析

想法一：按颜色拆贡献

这里应该是有一种小颜色大颜色的分块套路的。但是这个想法我只能解决全局路径的数量和，并不会落实到点的询问。

想法二：点分治

目前尚未归结出点分治适用的具体问题范围……不过这一题是可以用点分解决的。

考虑每一层点分树，我们只需要对它的节点处理贡献。这里的贡献分为两部分：重心答案；经过重心的路径对子树的贡献。

重心的答案只需要以它自身为根，遍历一边该层点分树即可。子树内的答案处理要略微麻烦一些，需要分颜色来考虑贡献。记$colCnt[i]$为所有以重心为起点的路径中，含有颜色$i$的路径条数。然后首先假定子树内所有点的答案都为$\sum colCnt[i]$，再容斥考虑重心到子树路径上的颜色所产生的贡献。

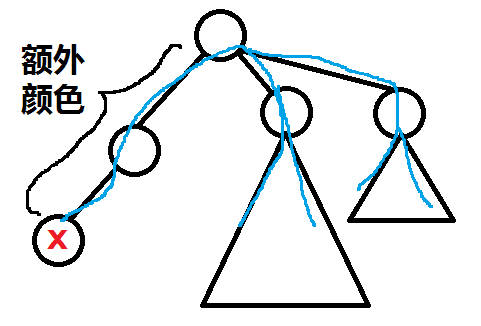
记当前点分树中除去正在处理的子树的大小为$outTot$，那么对于子树内点$x$，由于它具有颜色$c[x]$，所以对自身的答案有一个$outTot-colCnt[c[x]]$的贡献。并且，这一个贡献对于$x$的子树也是一概适用的，所以这一个标记要差分式地下传。

整体思路就是这些。这一题的点分涉及到例如“子树结构的重定向”或是“两个颜色桶并存”的一些细节问题，所以实现上面可能有一定的难度。

（话说这题的码风怎么这么丑）

 #include<bits/stdc++.h>
 typedef long long ll;
 const int maxn = ;
 const int maxm = ;

 ll ans[maxn];
 int n,bloTot,outTot,c[maxn];
 int size[maxn],son[maxn],root;
 int edgeTot,head[maxn],nxt[maxm],edges[maxm];
 int cols,cnt,cl,col[maxn],colTmp[maxn],colTim[maxn],colCnt[maxn],subCnt[maxn];
 bool colEx[maxn],divEx[maxn];

 int read()
 {
     char ch = getchar();
     int num = , fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
 void addedge(int u, int v)
 {
     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
     edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;
 }
 void getRoot(int x, int fa)
 {
     size[x] = , son[x] = ;
     for (int i=head[x]; i!=-; i=nxt[i])
     {
         int v = edges[i];
         if (divEx[v]||v==fa) continue;
         getRoot(v, x), size[x] += size[v];
         son[x] = std::max(son[x], size[v]);
     }
     son[x] = std::max(son[x], bloTot-size[x]);
     if (son[x] < son[root]) root = x;
 }
 void colDfs(int x, int fa, int *cnt)
 {
     if (!colEx[c[x]]) colEx[c[x]] = , col[++cols] = c[x];
     if ((++colTim[c[x]])==) cnt[c[x]] += size[x];
     for (int i=head[x]; i!=-; i=nxt[i])
         if ((!divEx[edges[i]])&&(edges[i]!=fa))
             colDfs(edges[i], x, cnt);
     --colTim[c[x]];
 }
 void colClear()
 {
     for (int i=; i<=cl; i++) colEx[colTmp[i]] = ;
     cols = ;
 }
 void modify(int x, int fa, ll tag)
 {
     if ((++colTim[c[x]])==) tag += outTot-colCnt[c[x]];
     ans[x] += tag+cnt;
     for (int i=head[x]; i!=-; i=nxt[i])
     {
         int v = edges[i];
         if (v==fa||divEx[v]) continue;
         modify(v, x, tag);
     }
     --colTim[c[x]];
 }
 void calc(int rt)　　　　　　//核心操作在这里
 {
     colClear(), getRoot(rt, );
     colDfs(rt, , colCnt);
     cnt = , cl = cols;
     for (int i=; i<=cols; i++)
         cnt += colCnt[col[i]], colTmp[i] = col[i];
     ans[rt] += cnt;
     for (int i=head[rt]; i!=-; i=nxt[i])
     {
         int v = edges[i];
         if (divEx[v]) continue;
         for (int j=; j<=cl; j++) subCnt[colTmp[j]] = ;　　//及时清除数组
         colClear();
         colEx[c[rt]] = ;
         colDfs(v, rt, subCnt);　　　　　　　　　　//统计子树内的含颜色i路径条数
         colEx[c[rt]] = ;
         colCnt[c[rt]] -= size[v], cnt -= size[v];　　　//除去重心出发的路径
         for (int j=; j<=cols; j++)
         {
             colCnt[col[j]] -= subCnt[col[j]];　　//除去子树内的路径（因为考虑子树外路径）
             cnt -= subCnt[col[j]];
         }
         outTot = size[rt]-size[v], modify(v, rt, );　　//对子树内累加贡献
         colCnt[c[rt]] += size[v], cnt += size[v];　　　　//恢复处理子树前状态
         for (int j=; j<=cols; j++)
         {
             colCnt[col[j]] += subCnt[col[j]];
             cnt += subCnt[col[j]];
         }
     }
     for (int i=; i<=cl; i++)
         colCnt[colTmp[i]] = ;　　　　　　//colTmp[]的作用；清空colCnt[]
 }
 void deal(int rt)
 {
     calc(rt), divEx[rt] = ;
     for (int i=head[rt]; i!=-; i=nxt[i])
     {
         int v = edges[i];
         if (divEx[v]) continue;
         root = , bloTot = size[v];
         getRoot(v, ), deal(root);
     }
 }
 int main()
 {
     memset(head, -, sizeof head);
     n = read(), son[] = n;
     for (int i=; i<=n; i++) c[i] = read();
     for (int i=; i<n; i++) addedge(read(), read());
     bloTot = n, getRoot(, ), deal(root);
     for (int i=; i<=n; i++) printf("%lld\n",ans[i]);
     return ;
 }

END