POJ 1656 Counting Black

Counting Black

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9772		Accepted: 6307

Description

There is a board with 100 * 100 grids as shown below. The left-top gird is denoted as (1, 1) and the right-bottom grid is (100, 100). 

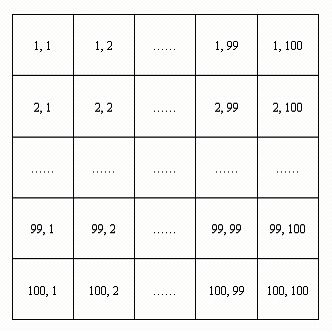
We may apply three commands to the board:

1.	WHITE  x, y, L     // Paint a white square on the board,

                           // the square is defined by left-top grid (x, y)

                           // and right-bottom grid (x+L-1, y+L-1)

2.	BLACK  x, y, L     // Paint a black square on the board,

                           // the square is defined by left-top grid (x, y)

                           // and right-bottom grid (x+L-1, y+L-1)

3.	TEST     x, y, L    // Ask for the number of black grids

                            // in the square (x, y)- (x+L-1, y+L-1) 

In the beginning, all the grids on the board are white. We apply a series of commands to the board. Your task is to write a program to give the numbers of black grids within a required region when a TEST command is applied. 

Input

The first line of the input is an integer t (1 <= t <= 100), representing the number of commands. In each of the following lines, there is a command. Assume all the commands are legal which means that they won't try to paint/test the grids outside the board.

Output

For each TEST command, print a line with the number of black grids in the required region.

Sample Input

5
BLACK 1 1 2
BLACK 2 2 2
TEST 1 1 3
WHITE 2 1 1
TEST 1 1 3

Sample Output

7
6
题目大意：输入n代表有n行指令，每行指令包括一个字符串cmd和三个数字x,y,nLen,如果cmd为“BLACK”表示将以x,y为左上角的边长为nLen的正方形里面的方块全部变成黑色，如果cmd为“WHITE”表示将以x,y为左上角的边长为nLen的正方形里面的方块全部变成白色，如果cmd为“TEST”则查询以x,y为左上角的边长为nLen的正方形里面的黑色方块共有多少个。
解题方法：而为树状数组。

#include <stdio.h>
#include <iostream>
#include <string.h>
using namespace std;

int maze[][];
int color[][];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int y, int n)
{
    if (color[x][y] == n)
    {
        return ;
    }
    color[x][y] = n;
    for (int i = x; i <= ; i += lowbit(i))
    {
        for (int j = y; j <= ; j += lowbit(j))
        {
            maze[i][j] += n;
        }
    }
}

int getsum(int x, int y)
{
    int sum = ;
    for (int i = x; i >= ; i -= lowbit(i))
    {
        for (int j = y; j >= ; j -= lowbit(j))
        {
            sum += maze[i][j];
        }
    }
    return sum;
}

int main()
{
    int n;
    int x, y, nLen;
    char cmd[];
    scanf("%d", &n);
    memset(color, -, sizeof(color));
    while(n--)
    {
        scanf("%s%d%d%d", cmd, &x, &y, &nLen);
        if (strcmp(cmd, "BLACK") == )
        {
            for (int i = x; i < x + nLen; i++)
            {
                for (int j = y; j < y + nLen; j++)
                {
                    add(i, j, );
                }
            }
        }
        else
        {
            if (strcmp(cmd, "WHITE") == )
            {
                for (int i = x; i < x + nLen; i++)
                {
                    for (int j = y; j < y + nLen; j++)
                    {
                        add(i, j, -);
                    }
                }
            }
            else
            {
                printf("%d\n", getsum(x + nLen - , y + nLen - ) - getsum(x - , y + nLen - ) - getsum(x + nLen - , y - ) + getsum(x - , y - ));
            }
        }
    }
    return ;
}