GBDT算法简述

提升决策树GBDT

梯度提升决策树算法是近年来被提及较多的一个算法，这主要得益于其算法的性能，以及该算法在各类数据挖掘以及机器学习比赛中的卓越表现，有很多人对GBDT算法进行了开源代码的开发，比较火的是陈天奇的XGBoost和微软的LightGBM

一、监督学习

1、  监督学习的主要任务

监督学习是机器学习算法中重要的一种，对于监督学习，假设有m个训练样本：

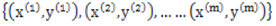
其中，

，如分类问题；也可以为连续值，如回归问题。在监督学习中利用训练样本训练出模型，该模型能够细线从样本特征 。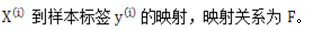

为了能够对映射F进行求解，通常对模型设置损失函数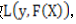

，并求的损失函数最小的情况下的映射为最好的映射。

对于一个具体的问题，如线性回归问题，其映射函数的形式为：

梯度下降法算法是求解最优化问题最简单、最直接的方法。梯度下降法是一种迭代的优化算法，对于优化问题：

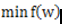
其基本步骤为：

1）  随机选择一个初始点

2）  重复以下过程：

决定下降的方向：

选择步长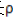

更新：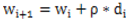

直到满足终止条件

梯度下降法的具体过程如下图所示：

2、  在函数空间的优化

以上是在指定的函数空间中对最优化函数进行搜索，那么，能否直接在函数空间中查找到最优的函数呢？根绝上述的梯度下降法的思路，对于模型的损失函数，为了

二、Boosting

1、  集成方法之Boosting

Boosting方法是集成学习中重要的一种方法，在集成学习方法中最主要的两种方法是Bagging和Boosting,在bagging中，通过对训练样本重新采样的方法得到不同的训练样本集，在这些新的训练样本集上分别训练学习器，最终合并每一个学习器的结果，作为最终的学习结果，Bagging方法的具体过程如下图所示：

在Bagging方法中最重要的算法为随机森林RF算法。由以上的图中可以看出，在Bagging方法中，b个学习器之间彼此是相互独立的，这样的特点使得Bagging方法更容易并行。与bagging不同的是，在Boosting算法中，学习器之间是存在先后顺序的，同时，每一个样本是都有权重的，初始时，每一个样本的权重都是相等的，首先，第1个学习器对训练样本进行学习，当学习完成后，增大错误样本的权重，同时减小正确样本的权重，再利用第2个学习器对其进行学习，依次进行下去，最终得到b个学习器，最终，合并这b个学习器的结果，同时，与Bagging中不同的是，每个学习器的权重也不一样，Boosting方法的具体过程如下图所示：

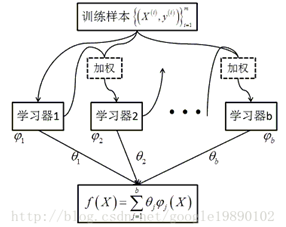
在Boosting方法中，最重要的方法包括：Adaboost和GBDT。

GB,梯度提升，通过进行M次迭代，每次迭代产生一个回归树模型，我们需要让每次迭代生成的模型对训练集的损失函数最小，而如何让损失函数越来越小呢？我们采用梯度下降的方法，在每次迭代时通过损失函数的负梯度方向移动来使得损失函数越来越小，这样我们就可以得到越来越精确的模型。

假设GBDT模型T有4棵回归树构成：t1,t2,t3,t4,样本标签Y(y1,y2,y3,….,yn)

设定该模型的误差函数为L，并且为SquaredError，则整体样本的误差推导如下：

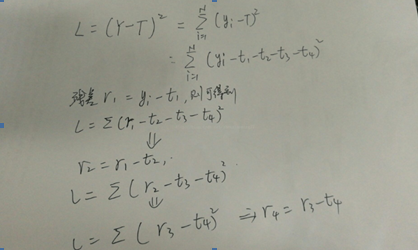
对于首颗树，可以看出，拟合的就是训练样本的标签，并且得到t1预测后的残差，从误差函数的公式中可以看出，后面的残差r2=r1-t2,r3=r2-t3,r4=r3-t4……,由此可以得出，后面的回归树t2,t3,t4创建时都是为了拟合前一次留下的残差，可以看出，残差不断在减小，直至达到可接受的阈值为止。

对于梯度版本，采用误差函数的当前负梯度值作为当前模型预测留下的残差，因此创建新的一棵回归树来拟合该残差，更新后，整体gbdt模型的残差将进一步降低，也带来L的不断降低。

Gbdt树分为两种，

（1）       残差版本

残差其实就是真实值和预测值之间的差值，在学习的过程中，首先学习一棵回归树，然后将“真实值-预测值”得到残差，再把残差作为一个学习目标，学习下一棵回归树，依次类推，直到残差小于某个接近0的阈值或回归树数目达到某一阈值。其核心思想是每轮通过拟合残差来降低损失函数。

总的来说，第一棵树是正常的，之后所有的树的决策全是由残差来决定。

（2）       梯度版本

与残差版本把GBDT说成一个残差迭代树，认为每一颗回归树都在学习前N-1棵树的残差不同，Gradient版本把GBDT说成一个梯度迭代树，使用梯度下降法求解，认为每一棵回归树都在学习前N-1棵树的梯度下降值。总的来说两者相同之处在于，都是迭代回归树，都是累加每棵树结果作为最终结果，每棵树都在学习前N-1棵树尚存的不足，从总体流程和输入输出上两者是没有区别的；

两者的不同主要每步迭代时，是否使用Gradient作为求解方法。前者不用gradient而用残差-残差是全局最优值，gradient是局部最优方向*步长，即前者每一步都在试图让结果变成最好，后者则每一步试图让结果更好一点。

两者优缺点。看起来前者更科学一点-有绝对最优方向不学，为什么舍近求远学一个局部最优方向呢？原因在于灵活性。前者最大的问题是，由于它依赖残差，损失函数一般固定为放映残差的均方差，因此很难处理纯回归问题之外的问题。而后者求解办法为梯度下降法，只要可求导的损失函数都可以使用。

总结：GBDT又叫MART，是一种迭代的决策树算法，该算法是由多棵决策树组成，所有树的结论累加起来做最终答案，它在被提出之初就和SVM一起被认为是泛化能力较强的算法。

GBDT中的树是回归树（不是分类树），GBDT用来做回归预测，调整后可以用于分类。

重要参数的设置及意义

问题：XGBoost和GBDT在调参的时候为什么树的深度很小就能达到很高的精度？

用xgboost/gbdt在调参的时候把树的最大深度调成6就有很高的精度了，但是用Desion Tree、RandomForest的时候，需要把树的深度调到15或更高。用RandomForest所需要的树的深度和DesionTree一样，我能理解，因为他是用disitionTree组合在一起的，相当于做了很多次的DecisionTree一样。但是xgboost/gbdt仅仅用梯度上升法就能达到很高的预测精度，使我惊讶到怀疑他是黑科技，请问下xgboost/gbdt是怎么做到的？她的节点和一般般的Desition不同吗？

答：Boosting主要关注降低偏差，因为boosting能给予泛化性能相当弱的学习器构建出很强的集成；Bagging主要关注降低偏差，因此它在不剪枝的决策树、神经网络等学习器上效果更为明显。

随机森林和GBDT都属于集成学习的范畴。集成学习下有两个重要的策略Bagging和Boosting

对于Bagging算法来说，由于我们会并行的训练很多不同的分类器的目的就是降低这个方差，因为，采用了相互独立的基分类器以后，h值自然就会靠近，所以对于每个分类器来说，目标就是如何降低这个偏差，所以我们就会采用很深的甚至不剪枝的决策树。

对于Boosting来说，每一步我们都会在上一轮的基础上更加拟合原始数据，所以可以保证偏差，所以对于每个基分类器来说，问题就在于如何选择方差更小的分类器，既简单的分类器，所以我们选择了深度很浅的决策树。