算法学习记录-图——最小生成树之prim算法

一个连通图的生成树是一个极小的连通子图，它包含图中全部的顶点（n个顶点），但只有n-1条边。

最小生成树：构造连通网的最小代价（最小权值）生成树。

prim算法在严蔚敏树上有解释，但是都是数学语言，很深奥。

最小生成树MST性质：假设N=（V,{E}）是一个连通网，U是顶点集V的一个非空子集。若（u,v）是一条具有最小权值（代价）的边，

其中u∈U，v∈V-U，则必存在一颗包含边（u,v）的最小生成树。

prim算法过程为：

假设N=（V,{E}）是连通图，TE是N上最小生成树中边的集合。算法从U={u₀}（u₀∈V），TE={}开始，

重复执行下述操作：

在所有u∈U，v∈V-U的边（u，v）∈E中找一条代价最小的边（u₀，v₀）并入集合TE，同时v₀ 并入U，直至U=V为止。

此时TE中必有n-1条边，则T=（V，{TE}）为N的最小生成树。

我以图为例，看看算法过程。

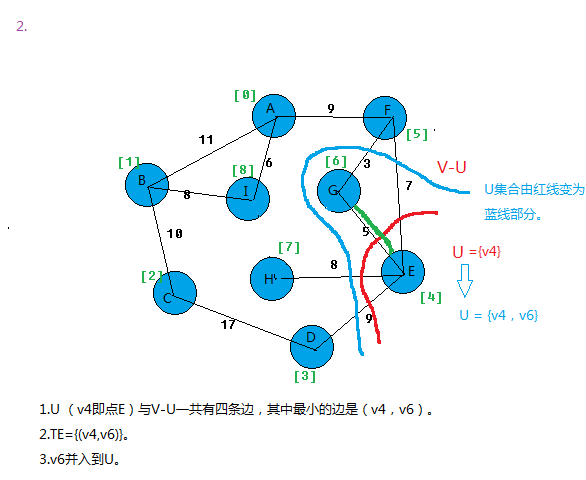
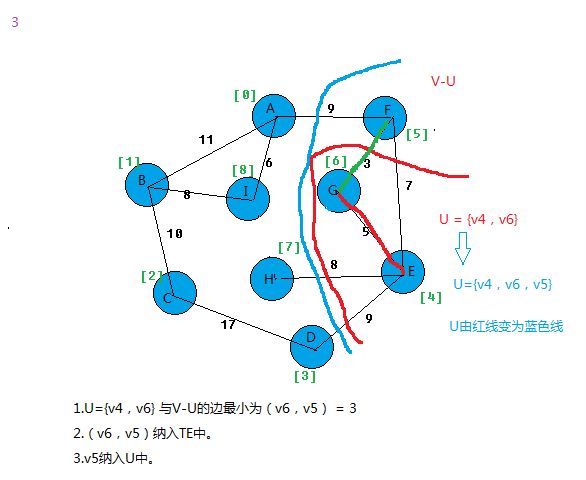
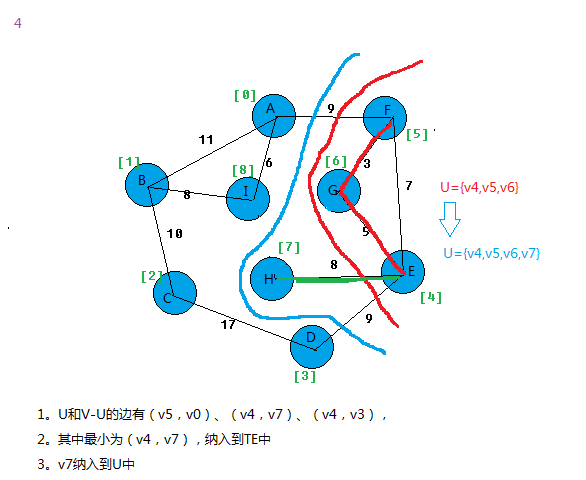
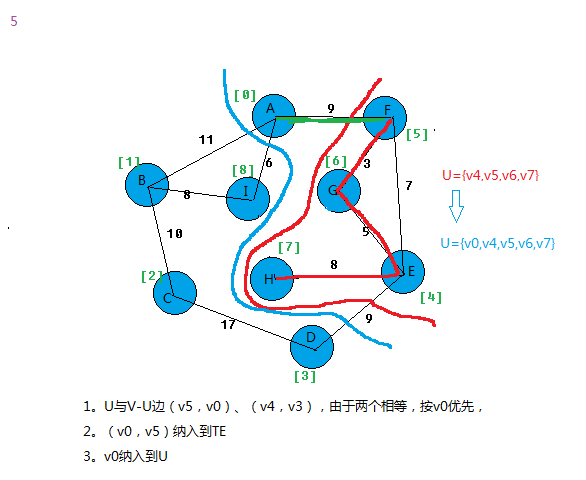
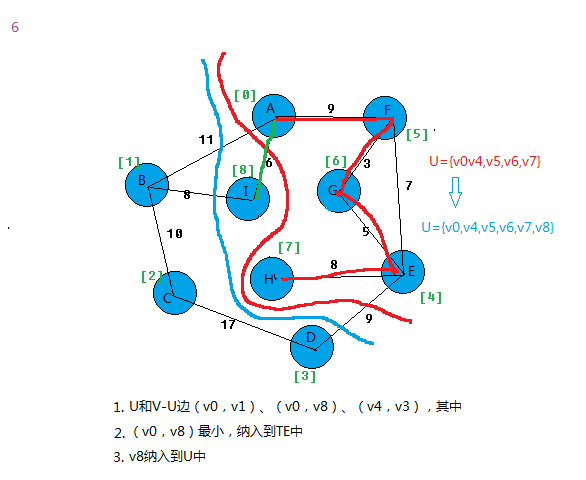
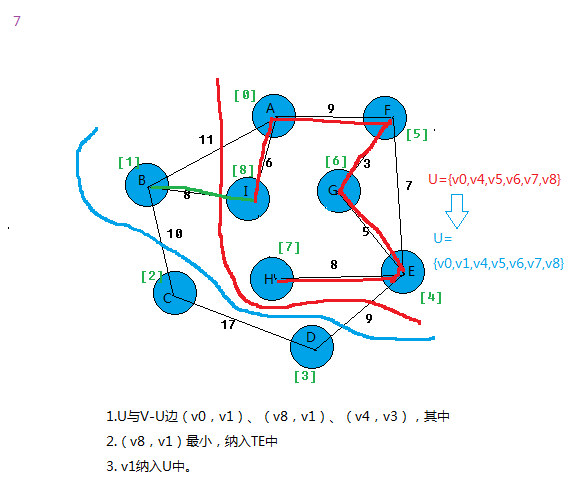
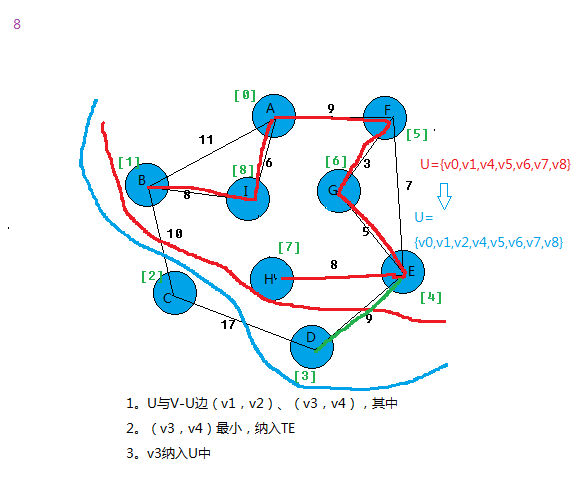
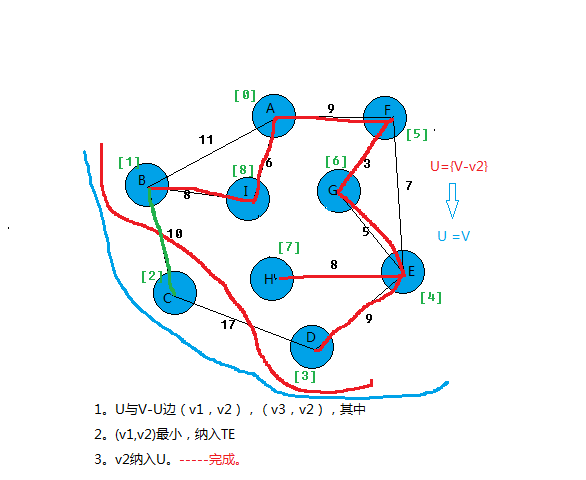
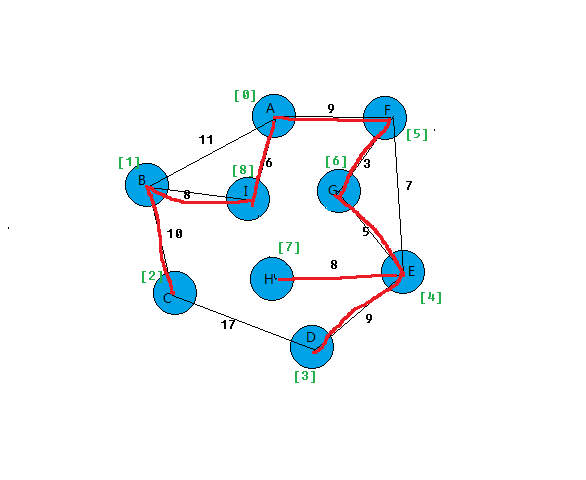
上面基本就把prim算法思想给表达出来。

代码部分：

这里我使用的是邻接矩阵来表示图，其中边的值就是权值。

#define MAXVEX 100
#define IFY 65535

typedef char VertexType;
typedef int  EdgeType;

//静态图-邻接矩阵
typedef struct {
    VertexType vexs[MAXVEX];
    EdgeType Mat[MAXVEX][MAXVEX];
    int numVexs,numEdges;
}MGraph;

VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'};

EdgeType g_init_edges[MAXVEX][MAXVEX] = {
    {,,IFY,IFY,IFY,,IFY,IFY,},    //'A'
    {,,,IFY,IFY,IFY,IFY,IFY,},  //'B'
    {IFY,,,,IFY,IFY,IFY,IFY,IFY},//'C'
    {IFY,IFY,,,,IFY,IFY,IFY,IFY},//'D'
    {IFY,IFY,IFY,,,,,,IFY},    //'E'
    {,IFY,IFY,IFY,,,,IFY,IFY},    //'F'
    {IFY,IFY,IFY,IFY,,,,IFY,IFY},    //'G'
    {IFY,IFY,IFY,IFY,,IFY,IFY,,IFY},    //'H'
    {,,IFY,IFY,IFY,IFY,IFY,IFY,},    //'I'
};

prim算法代码：

void prim(MGraph G,int num)
{
    int sum=;
    int min,i,j,k;
    int adjvex[MAXVEX];
    int lowcost[MAXVEX];

    lowcost[num] = ;
    adjvex[num] = ;

    for (i = ; i < G.numVexs;i++ )
    {
        if (num == i)
        {
            continue;
        }
        lowcost[i]=G.Mat[num][i];    //存放起始顶点到各个顶点的权值。
        adjvex[i] = num;
    }

    for (i=;i<G.numVexs;i++)
    {
        //1.找权最短路径
        //2.把权最短路径的顶点纳入已找到的顶点集合中，重新查看新集合中最短路径
        if(num == i)
        {
            continue;
        }
        min = IFY;
        j=;k=;
        while (j<G.numVexs)
        {
            if (lowcost[j] !=  && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j;

            }
            j++;
        }
        printf(" (%d,%d) --> ",adjvex[k],k);
        sum += G.Mat[adjvex[k]][k];
        lowcost[k]=;
        for (j=;j<G.numVexs;j++)
        {
            if (j == num)
            {
                continue;
            }
            if (lowcost[j] !=  && G.Mat[k][j] < lowcost[j])
            {
                lowcost[j] = G.Mat[k][j];
                adjvex[j]=k;
            }
        }
    }
    printf("\ntotal:sum=%d",sum);
}

我写的是一个可以指定入口的（即从哪个点）开始进行。测试每个入口，得到的路径应该是一样，且值也应该一样大。

其中两个辅助数组:

lowcost[]：用来存放 非U集合的点与U集合点的权值的最小值。其【x】里面的数字x，表示U中到V中顶点Vx的最小权值。（每次都会更新比较，保证其最小。）

　　　　　　而归入到U集合的点，对应的lowcost中的元素是为0；之后就不再做比较。

adjvex[]：在每次归入新顶点后，都要对U与非U集合中权值比较，保持lowcost中的值为最小。此时改变的lowcost中的某个元素（即新纳入的顶点到非U集合的权值更小）

　　　　　　此时，将改变的lowcost中序号x，将新纳入的顶点Vt与原先U集合中与之相连的点的序号存入adjvex【x】。这样 adjvex【x】中，x就是那些个要更新的

　　　　　　lowcost【x】，adjvex【x】存放就是原先点。

这也方便查找新加入的边（adjvex【k】，k）。

　　　

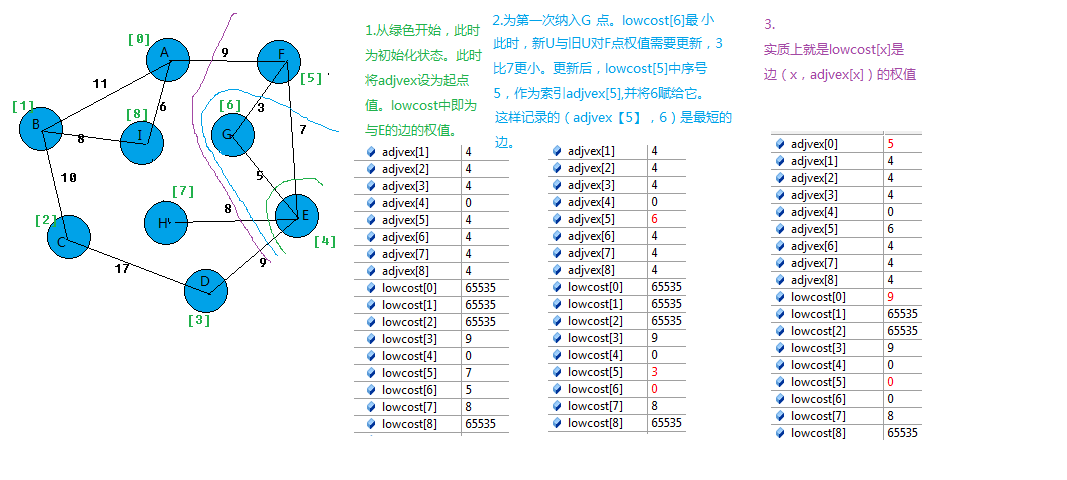
基本上可以看出，adjvex【】作用：

　　实质上lowcost[x] 是 边（x，adjvex[x]）的权值。明白这一点，程序就非常好理解了。

完整程序：

// grp-mat-bfs-self.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <stdlib.h>

#define MAXVEX 100
#define IFY 65535

typedef char VertexType;
typedef int  EdgeType;

bool g_visited[MAXVEX];

VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'};

EdgeType g_init_edges[MAXVEX][MAXVEX] = {
    {,,IFY,IFY,IFY,,IFY,IFY,},    //'A'
    {,,,IFY,IFY,IFY,IFY,IFY,},  //'B'
    {IFY,,,,IFY,IFY,IFY,IFY,IFY},//'C'
    {IFY,IFY,,,,IFY,IFY,IFY,IFY},//'D'
    {IFY,IFY,IFY,,,,,,IFY},    //'E'
    {,IFY,IFY,IFY,,,,IFY,IFY},    //'F'
    {IFY,IFY,IFY,IFY,,,,IFY,IFY},    //'G'
    {IFY,IFY,IFY,IFY,,IFY,IFY,,IFY},    //'H'
    {,,IFY,IFY,IFY,IFY,IFY,IFY,},    //'I'
};

EdgeType g_init_edges_bak[MAXVEX][MAXVEX] = {
    {,,IFY,IFY,IFY,,IFY,IFY,},    //'A'
    {,,,IFY,IFY,IFY,IFY,IFY,},  //'B'
    {IFY,,,,IFY,IFY,IFY,IFY,IFY},//'C'
    {IFY,IFY,,,,IFY,IFY,IFY,IFY},//'D'
    {IFY,IFY,IFY,,,,,,IFY},    //'E'
    {,IFY,IFY,IFY,,,,IFY,IFY},    //'F'
    {IFY,IFY,IFY,IFY,,,,IFY,IFY},    //'G'
    {IFY,IFY,IFY,IFY,,IFY,IFY,,IFY},    //'H'
    {,,IFY,IFY,IFY,IFY,IFY,IFY,},    //'I'
};
//==========================================================================
//静态图-邻接矩阵
typedef struct {
    VertexType vexs[MAXVEX];
    EdgeType Mat[MAXVEX][MAXVEX];
    int numVexs,numEdges;
}MGraph;

//====================================================================
//打印矩阵
void prt_maxtix(EdgeType *p,int vexs)
{
    int i,j;
    for (i=;i<vexs;i++)
    {
        printf("\t");
        for (j=;j<vexs;j++)
        {
            if( (*(p + MAXVEX*i + j)) == IFY)
            {
                printf("  $ ");
            }
            else
            {
                printf(" %2d ", *(p + MAXVEX*i + j));
            }
        }
        printf("\n");
    }
}

//check the number of vextex
int getVexNum(VertexType *vexs)
{
    VertexType *pos = vexs;
    int cnt=;
    while(*pos <= 'Z' && *pos >= 'A')
    {
        cnt++;
        pos++;
    }
    return cnt;
}

bool checkMat(EdgeType *p,VertexType numvex)
{
    int i,j;
    for (i=;i<numvex;i++)
    {
        for(j=i+;j<numvex;j++)
        {
            //printf("[%d][%d] = %d\t",i,j,*(p + MAXVEX*i + j));
            //printf("[%d][%d] = %d\n",j,i,*(p + MAXVEX*j + i));
            if (*(p + MAXVEX*i + j) != *(p + MAXVEX*j +i) )
            {
                printf("ERROR:Mat[%d][%d] or Mat[%d][%d] not equal!\n",i,j,j,i);
                return false;
            }
        }
    }
    return true;
}

void init_Grp(MGraph *g,VertexType *v,EdgeType *p)
{
    int i,j;
    // init vex num
    (*g).numVexs = getVexNum(v);

    //init vexter
    for (i=;i<(*g).numVexs;i++)
    {
        (*g).vexs[i]=*v;
        v++;
    }

    //init Mat
    for (i=;i<(*g).numVexs;i++)
    {
        for (j=;j<(*g).numVexs;j++)
        {
            (*g).Mat[i][j] = *(p + MAXVEX*i + j);
        }
    }
    if(checkMat(&((*g).Mat[][]),(*g).numVexs) == false)
    {
        printf("init error!\n");
        exit();
    }
}

void prim(MGraph G,int num)
{
    int sum=;
    int min,i,j,k;
    int adjvex[MAXVEX];
    int lowcost[MAXVEX];

    lowcost[num] = ;
    adjvex[num] = ;

    for (i = ; i < G.numVexs;i++ )
    {
        if (num == i)
        {
            continue;
        }
        lowcost[i]=G.Mat[num][i];    //存放起始顶点到各个顶点的权值。
        adjvex[i] = num;
    }

    for (i=;i<G.numVexs;i++)
    {
        //1.找权最短路径
        //2.把权最短路径的顶点纳入已找到的顶点集合中，重新查看新集合中最短路径
        if(num == i)
        {
            continue;
        }
        min = IFY;
        j=;k=;
        while (j<G.numVexs)
        {
            if (lowcost[j] !=  && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j;

            }
            j++;
        }
        printf(" (%d,%d) --> ",adjvex[k],k);
        sum += G.Mat[adjvex[k]][k];
        lowcost[k]=;
        for (j=;j<G.numVexs;j++)
        {

            if (lowcost[j] !=  && G.Mat[k][j] < lowcost[j])
            {
                lowcost[j] = G.Mat[k][j];
                adjvex[j]=k;
            }
        }

    }
    printf("total:sum=%d\n",sum);
}

int _tmain(int argc, _TCHAR* argv[])
{
    MGraph grp;
    //init
    init_Grp(&grp,g_init_vexs,&g_init_edges[][]);
    //print Matix
    prt_maxtix(&grp.Mat[][],grp.numVexs);

    //prim(grp,4);
    int i;
    for (i=;i<grp.numVexs;i++)
    {
        prim(grp,i);
    }
    //prim(grp,3);

    getchar();
    return ;
}

测试结果：

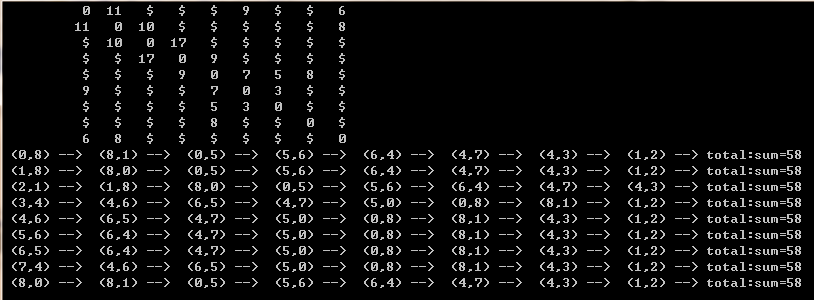
最小生成树一样，而且总权值也一样。