JSOI2004 平衡点 / 吊打XXX

题目描述

有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

输入输出格式

输入格式：

文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )

输出格式：

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。

输入输出样例

输入样例 1：

3

0 0 1

0 2 1

1 1 1

输出样例 1：

0.577 1.000

数据范围

1≤n≤1000

-10000≤x,y≤10000, 0<w≤1000

Solution

首先看看这个题目（貌似像物理题）。

当x点确定时，所有重物的重力势能之和最小，由于所有的绳子是一样长的，所以重的物体离地面要近一些，必须使得桌面上的那一截绳子最短，也就是离x点越近。

那么我们不难列出这个式子：



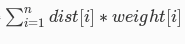
其中dist为点到x的距离，weight为点上物体的重量

当上述式子最小时，即为答案x。

贴代码

#include<bits/stdc++.h>
using namespace std;
const int Maxn=1005;
struct Lemon
{
    int x,y,m;
}point[Maxn];
int n;
double ansx,ansy;
void read()
{
    int allx=0,ally=0;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",&point[i].x,&point[i].y,&point[i].m);
        allx+=point[i].x;
        ally+=point[i].y;
    }
    ansx=double(allx)/double(n);
    ansy=double(ally)/double(n);
    return ;
}
double get(double x,double y)
{
    double sum=0;
    for(int i=1;i<=n;i++)
    {
        double lex=point[i].x-x;
        double ley=point[i].y-y;
        sum+=sqrt(lex*lex+ley*ley)*point[i].m;
    }
    return sum;
}
double ans=1000000000000009,t;//ans不要开太小，被这个坑了好久
const double delta=0.9969;
void fire()
{
    double menx=ansx;
    double meny=ansy;
    t=1218.0;
    while(t>1e-14)
    {
        double xtemp=ansx+(rand()*2-RAND_MAX)*t;
        double ytemp=ansy+(rand()*2-RAND_MAX)*t;
        double newans=get(xtemp,ytemp);
        double DE=newans-ans;
        if(DE<0)
        {
        	menx=xtemp;
        	meny=ytemp;
        	ansx=xtemp;
        	ansy=ytemp;
        	ans=newans;
        }
        else if(exp(-DE/t)*RAND_MAX>rand())
        {
            menx=xtemp;
            meny=ytemp;
        }
        t*=delta;
    }
}
int main()
{
    read();
    fire();
    fire();
    fire();
    fire();
    printf("%.3lf %.3lf",ansx,ansy);
    return 0;
}