搜索入门之dfs--经典的迷宫问题解析

今天来谈一下dfs的入门，以前看到的dfs入门，那真的是入门吗，都是把dfs的实现步骤往那一贴，看完是知道dfs的步骤了，但是对于代码实现还是没有概念。今天准备写点自己的心得，真的是字面意思--入门。

DFS，即深度优先搜索，是一种每次搜索都向尽可能深的地方去搜索，到达尽头时再回溯进行其他结点去搜索的搜索策略。形象的说，这是一种“不撞南墙不回头”的策略。

其实也就是遍历，只不过不像一个线性数组的遍历那么直观罢了。说到回溯，每次看到这个词我都得思考一会，到底是怎么用栈进行回溯的呢？今天实际操作了一次bfs，才发现妹的，这个事都是交给编译器去完成的(只要写的是递归形式)...当然了，非递归形式的dfs实现，肯定是要自己做栈的...

---

迷宫问题

迷宫问题是dfs入门的一个经典问题，这里就以HDOJ 1010 Tempter of Bone 来谈谈如何实际运用dfs。

http://acm.hdu.edu.cn/showproblem.php?pid=1010

题目大意：　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　 S.X.

　　　　　　　　　　　　　　　　　　　　　　　　　 ..X.

　　　　　　　　　　　　　　　　　　　　　　　　　 ..XD

　　　　　　　　　　　　　　　　　　　　　　　　　 ....

给出一个由以上四种符号组成的“迷宫”，‘.’代表可以通行的块，‘X’代表墙不能通过，‘S’代表起点，‘D’代表终点，每秒都必须且只能走一步(上、下、左、右)，判断能否恰好在第T秒，到达终点D。其中每次走过的‘.’块都会立刻消失不能再走。

当然了，算法就是dfs了，其实也就是暴力枚举，对走的每一步都进行4个方向上的分支判断，再加上一定的剪枝，舍去一些明显不合题意的结果，以满足时间上的要求。

先贴上代码吧：

 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 using namespace std;
 char map[][];//输入的迷宫矩阵
 int dir[][] = {{, }, {, }, {-, }, {, -}};//4个方向
 int OK = ;
 int N, M, T, si, sj, di, dj;
 int dfs(int si, int sj, int cnt)
 {
     if (si <=  || sj <=  || si > N || sj > M)//超出边界就说明这条路已经死了，则返回
     {
         return ;
     }
     if (si == di && sj == dj && cnt == T)//找到终点就返回，把标志位置为1
     {
         OK = ;
     }
     if (OK)
     {
         return ;
     }
     int temp = T - cnt - abs(di - si) - abs(dj - sj);//这里就是剪枝，开始没写这里，Time Limit Exceeded了十几次...下面细谈
     if (temp <  || temp & )
     {
         return ;
     }
     for (int i = ; i < ; ++i)//对走到的每个结点都进行四个方向的探索
     {
         if (map[si+dir[i][]][sj+dir[i][]] != 'X')
         {
             map[si+dir[i][]][sj+dir[i][]] = 'X';//走过的路不能走，就先置为墙
             dfs(si+dir[i][], sj+dir[i][], cnt + );
             map[si+dir[i][]][sj+dir[i][]] = '.';//探索下一条路时，这个结点要恢复成可以走的状态
         }
     }
     return ;
 }
 int main()
 {
     while(cin >> N >> M >> T)
     {
         int wall = ;
         OK = ;
         if (N ==  && M ==  && T == )
         {
             break;
         }
         for (int i = ; i <= N; ++i)
         {
             for (int j = ; j <= M; ++j)
             {
                 cin >> map[i][j];//这里开始还写的scanf("%c", &map[i][j]);蠢的不谈了...  不过可以这样在for(i)的循环里面写 scanf("%s", &map[i]);
                 if (map[i][j] == 'S')
                 {
                     si = i;
                     sj = j;
                 }else if (map[i][j] == 'D')
                 {
                     di = i;
                     dj = j;
                 }else if (map[i][j] == 'X')
                 {
                     wall++;
                 }
             }
         }
         if (N * M - wall <= T)//一个小剪枝
         {
             cout << "NO" << endl;
             continue;
         }
         map[si][sj] = 'X';
         dfs(si, sj, );
         if (OK)
         {
             cout << "YES" << endl;
         }else
         {
             cout << "NO" << endl;
         }
     }
     return ;
 }

先借助代码谈一下dfs的过程：

从S开始，i = 0，往右探索，只要没有return，就一直往右走，return了就回溯，回溯的过程呢，就是从i = 0转到i = 1了，这就是回溯的实现过程...

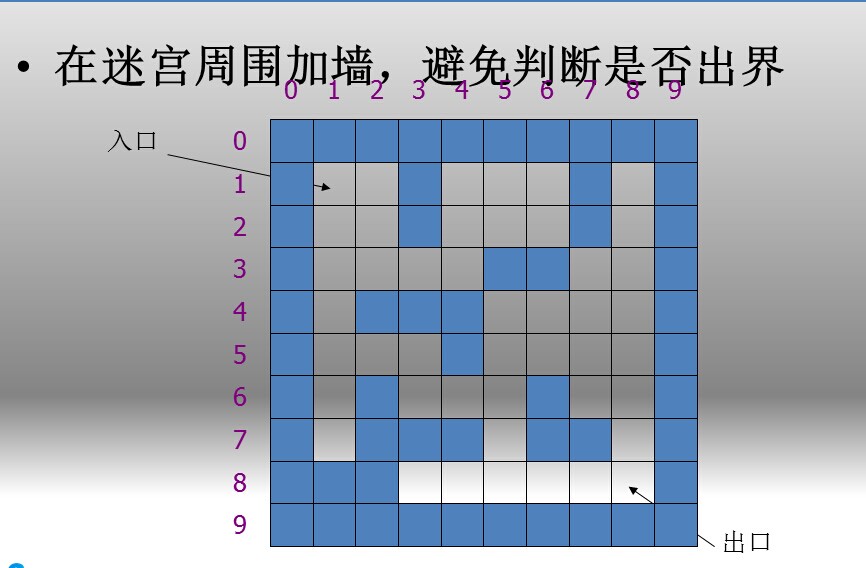
一个小技巧，初始化这个迷宫矩阵的时候，i = 0 ， j = 0， i = n + 1， j = m + 1都进行初始化，但是不存储数据，这样相当于在迷宫外面的四面都加上了墙，这样在dfs过程中就不用判断是否出界了...

下面谈一下剪枝：

1、如果可走的块数小于T，则肯定不能到达，这就是main()中的那个小剪枝

2、奇偶性剪枝：

可以把map看成这样：

0 1 0 1 0 1

1 0 1 0 1 0

0 1 0 1 0 1

1 0 1 0 1 0

0 1 0 1 0 1

从为 0 的格子走一步，必然走向为 1 的格子

从为 1 的格子走一步，必然走向为 0 的格子

即：

　　0 ->1或1->0 必然是奇数步

　　0->0 走1->1 必然是偶数步

 

结论：

　　所以当遇到从 0 走向 0 但是要求时间是奇数的，或者， 从 1 走向 0 但是要求时间是偶数的 都可以直接判断不可达！

这就是dfs中那个剪枝，也就是最主要的剪枝，其中用了&与运算来判断是不是偶数...

---

提醒：

算法中最基本和常用的是搜索，这里要说的是，有些初学者在学习这些搜索基本算法是不太注意剪枝，这是十分不可取的，因为所有搜索的题目给你的测试用例都不会有很大的规模，你往往察觉不出程序运行的时间问题，但是真正的测试数据一定能过滤出那些没有剪枝的算法。

实际上参赛选手基本上都会使用常用的搜索算法，题目的区分度往往就是建立在诸如剪枝之类的优化上了。 ”