LGP5075【JSOI2012】分零食

、

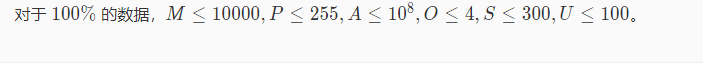
• 题解：

  • 令$F$为欢乐度$f(x) = Ox^2 + Sx + U$的生成函数，常数项为$0$；
  • 令$G(x) = \sum_{i=0}^{A} F^i (x) $
  • $ans = [x^M]G;$
  • 模数比较麻烦所以我用的分治求:
  • 如果现在要求$0$到$n-1$的$G_{n} = \sum_{i=0}^{n-1}F^{i}$和$F_{n} = F^{n} $，假设n为偶数；
  • 那么分治求出关于$n/2$的答案$G_{\frac{n}{2}}$和$F_{\frac{n}{2}}$
  • $$G_{n} = (F_{\frac{n}{2}}+1)G_{\frac{n}{2}}  , F_{n} = F_{\frac{n}{2}}^2$$
  • 如果$n$是奇数先算用上述操作算$n-1$，再把$F_{n-1}$补加给$G_{n-1}$得到$G_{n}$,最后$F_{n-1}$另外乘一次得到$F_{n}$；
  • 和快速幂的思想差不多；

  •  #include<bits/stdc++.h>
     #define ld double
     using namespace std;
     const int N=;
     const ld pi=acos(-);
     int M,P,A,O,S,U,len,L,rev[N];
     struct C{
         ld x,y;
         C(ld _x=,ld _y=):x(_x),y(_y){};
         C operator +(const C&A)const{return C(x+A.x,y+A.y);}
         C operator -(const C&A)const{return C(x-A.x,y-A.y);}
         C operator *(const C&A)const{return C(x*A.x-y*A.y,x*A.y+y*A.x);}
         C operator /(const ld&A)const{return C(x/A,y/A);}
     }f[N],g[N],t[N];
     int cal(int x){return (O*x*x+S*x+U)%P;}
     void fft(C*a,int f){
         for(int i=;i<len;++i)if(i<rev[i])swap(a[i],a[rev[i]]);
         for(int i=;i<len;i<<=){
             C wn=C(cos(pi/i),f*sin(pi/i));
             for(int j=;j<len;j+=i<<){
                 C w=C(,);
                 for(int k=;k<i;++k,w=w*wn){
                     C x=a[j+k],y=w*a[j+k+i];
                     a[j+k]=x+y,a[j+k+i]=x-y;
                 }
             }
         }
         if(!~f)for(int i=;i<len;++i){
             a[i]=a[i]/len;
             a[i].x=int(a[i].x+0.1)%P;
             a[i].y=;
         }
     }
     void solve(int A){
         if(A==){g[].x=;return;}
         solve(A>>);
         fft(f,);fft(g,);
         for(int j=;j<len;++j)g[j]=g[j]*(f[j]+C(,)),f[j]=f[j]*f[j];
         fft(f,-);fft(g,-);
         for(int j=M+;j<len;++j)f[j].x=g[j].x=;
         if(A&){
             for(int j=;j<=M;++j)g[j].x=(int)(g[j].x+f[j].x+0.1)%P;
             fft(f,);for(int j=;j<len;++j)f[j]=f[j]*t[j];
             fft(f,-);for(int j=M+;j<len;++j)f[j].x=;
         }
     }
     int main(){
     //    freopen("P5075.in","r",stdin);
     //    freopen("P5075.out","w",stdout);
         scanf("%d%d%d%d%d%d",&M,&P,&A,&O,&S,&U);
         for(int i=;i<=M;++i)t[i].x=f[i].x=cal(i%P);
         for(len=;len<=M<<;len<<=,L++);
         for(int i=;i<len;++i)rev[i]=(rev[i>>]>>)|((i&)<<(L-));
         fft(t,);solve(min(A,M)+);
         printf("%d\n",(int)(g[M].x+0.1)%P);
         return ;
     }