可变多隐层神经网络的python实现
说明：这是我对网上代码的改写版本，目的是使它跟前一篇提到的使用方法尽量一致，用起来更直观些。
此神经网络有两个特点：
1、灵活性
非常灵活，隐藏层的数目是可以设置的，隐藏层的激活函数也是可以设置的
2、扩展性
扩展性非常好。目前只实现了一个学习方法：lm（Levenberg-Marquardt训练算法），你可以添加不同的学习方法到NeuralNetwork类
什么是最优化，可分为几大类？
答：Levenberg-Marquardt算法是最优化算法中的一种。最优化是寻找使得函数值最小的参数向量。它的应用领域非常广泛，如：经济学、管理优化、网络分析、最优设计、机械或电子设计等等。
根据求导数的方法，可分为2大类。第一类，若f具有解析函数形式，知道x后求导数速度快。第二类，使用数值差分来求导数。
根据使用模型不同，分为非约束最优化、约束最优化、最小二乘最优化。
什么是Levenberg-Marquardt算法？
答：它是使用最广泛的非线性最小二乘算法，中文为列文伯格-马夸尔特法。它是利用梯度求最大（小）值的算法，形象的说，属于“爬山”法的一种。它同时具有梯度法和牛顿法的优点。当λ很小时，步长等于牛顿法步长，当λ很大时，步长约等于梯度下降法的步长。
（本文基于win7 + python3.4）
一、先说说改动的部分
1) 改写了NetStruct类初始化函数
原来：
class NetStruct:
'''神经网络结构'''
def __init__(self, x, y, hidden_layers, activ_fun_list, performance_function = 'mse'):
现在：
class NetStruct:
'''神经网络结构'''
def __init__(self, ni, nh, no, active_fun_list):
# ni 输入层节点数（int）
# ni 隐藏层节点数（int 或 list）
# no 输出层节点数（int）
# active_fun_list 隐藏层激活函数类型（list）
好处：
初始化网络时更直观
2) 修改了NeuralNetwork类的train函数的参数
原来：
class NeuralNetwork:
def __init__(self, ...):
# ...
def train(self, method = 'lm'):
if(method == 'lm'):
self.lm()
现在：
class NeuralNetwork:
'''神经网络'''
def __init__(self, ...):
'''初始化'''
# ... def train(self, x, y, method = 'lm'):
'''训练'''
self.net_struct.x = x
self.net_struct.y = y
if(method == 'lm'):
self.lm()
好处：
使用训练（train）函数时更直观
3) 修改了sinSamples样例函数的错误
原代码会报错："x与y维度不一致"
4) 添加了部分注释
主要是为了更好地理解代码
二、再说说隐藏层的层数对误差的影响
效果图（peakSamples样例）
1) 两个隐藏层
误差：
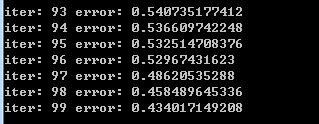
100次迭代后，误差一般收敛在（1.3， 0.3）这个区间
2) 三个隐藏层
误差：
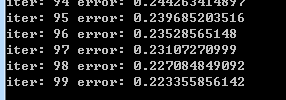
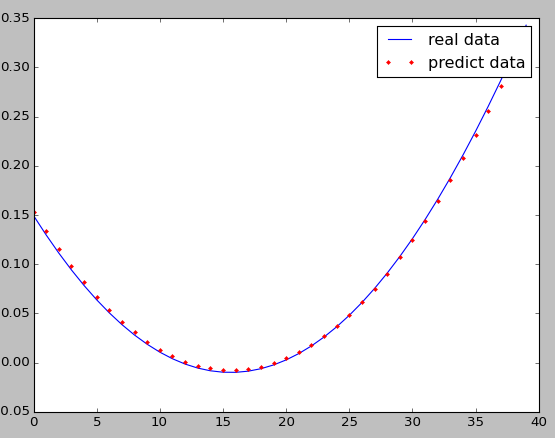
100次迭代后，误差一般收敛在（0.3， 0.1）这个区间
结论：对于peakSamples这个样例，采用三个隐藏层优于两个隐藏层（显然，这里没有考虑与测试各隐藏层神经元数目改变的情况）
注：还可以试试另外一个测试函数
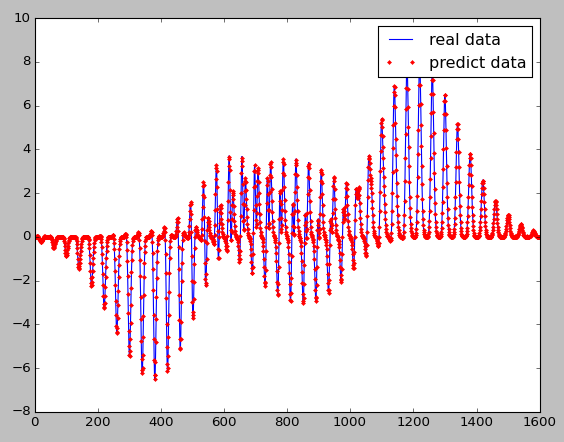
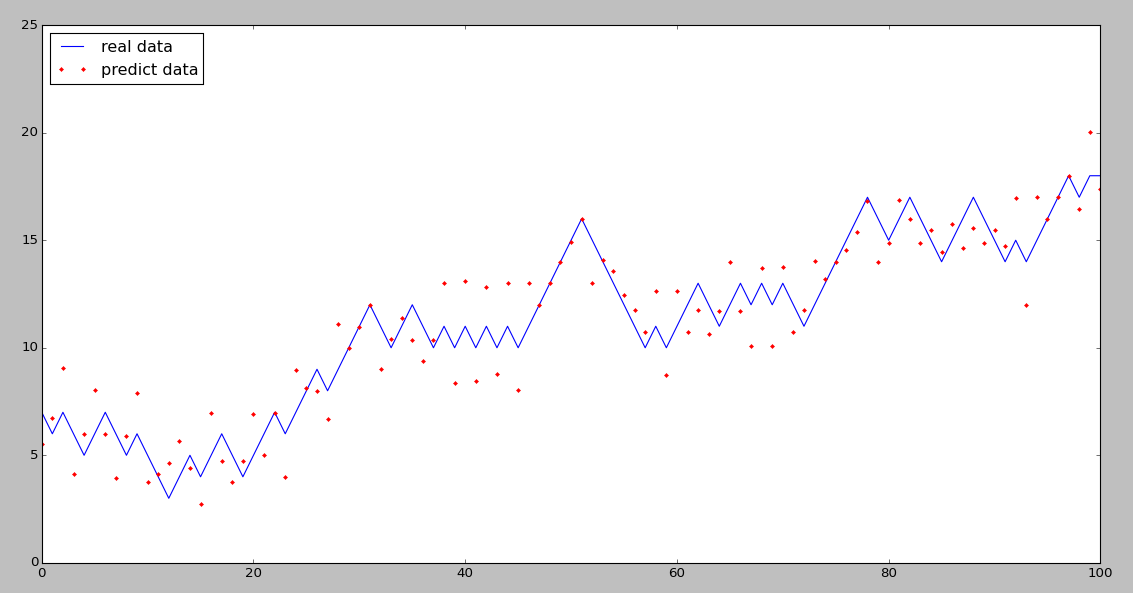
再附一个我用股票数据做的预测效果图 ：
完整代码：
# neuralnetwork.py
# modified by Robin 2015/03/03 import numpy as np
from math import exp, pow
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import sys
import copy
from scipy.linalg import norm, pinv class Layer:
'''层'''
def __init__(self, w, b, neure_number, transfer_function, layer_index):
self.transfer_function = transfer_function
self.neure_number = neure_number
self.layer_index = layer_index
self.w = w
self.b = b class NetStruct:
'''神经网络结构'''
def __init__(self, ni, nh, no, active_fun_list):
# ni 输入层节点（int）
# ni 隐藏层节点（int 或 list）
# no 输出层节点（int）
# active_fun_list 隐藏层激活函数类型（list）
# ==> 1
self.neurals = [] # 各层的神经元数目
self.neurals.append(ni)
if isinstance(nh, list):
self.neurals.extend(nh)
else:
self.neurals.append(nh)
self.neurals.append(no)
# ==> 2
if len(self.neurals)-2 == len(active_fun_list):
active_fun_list.append('line')
self.active_fun_list = active_fun_list
# ==> 3
self.layers = [] # 所有的层
for i in range(0, len(self.neurals)):
if i == 0:
self.layers.append(Layer([], [], self.neurals[i], 'none', i))
continue
f = self.neurals[i - 1]
s = self.neurals[i]
self.layers.append(Layer(np.random.randn(s, f), np.random.randn(s, 1), self.neurals[i], self.active_fun_list[i-1], i)) class NeuralNetwork:
'''神经网络'''
def __init__(self, net_struct, mu = 1e-3, beta = 10, iteration = 100, tol = 0.1):
'''初始化'''
self.net_struct = net_struct
self.mu = mu
self.beta = beta
self.iteration = iteration
self.tol = tol def train(self, x, y, method = 'lm'):
'''训练'''
self.net_struct.x = x
self.net_struct.y = y
if(method == 'lm'):
self.lm() def sim(self, x):
'''预测'''
self.net_struct.x = x
self.forward()
layer_num = len(self.net_struct.layers)
predict = self.net_struct.layers[layer_num - 1].output_val
return predict def actFun(self, z, active_type = 'sigm'):
''' 激活函数 '''
# activ_type: 激活函数类型有 sigm、tanh、radb、line
if active_type == 'sigm':
f = 1.0 / (1.0 + np.exp(-z))
elif active_type == 'tanh':
f = (np.exp(z) + np.exp(-z)) / (np.exp(z) + np.exp(-z))
elif active_type == 'radb':
f = np.exp(-z * z)
elif active_type == 'line':
f = z
return f def actFunGrad(self, z, active_type = 'sigm'):
'''激活函数的变化（派生）率'''
# active_type: 激活函数类型有 sigm、tanh、radb、line
y = self.actFun(z, active_type)
if active_type == 'sigm':
grad = y * (1.0 - y)
elif active_type == 'tanh':
grad = 1.0 - y * y
elif active_type == 'radb':
grad = -2.0 * z * y
elif active_type == 'line':
m = z.shape[0]
n = z.shape[1]
grad = np.ones((m, n))
return grad def forward(self):
''' 前向 '''
layer_num = len(self.net_struct.layers)
for i in range(0, layer_num):
if i == 0:
curr_layer = self.net_struct.layers[i]
curr_layer.input_val = self.net_struct.x
curr_layer.output_val = self.net_struct.x
continue
before_layer = self.net_struct.layers[i - 1]
curr_layer = self.net_struct.layers[i]
curr_layer.input_val = curr_layer.w.dot(before_layer.output_val) + curr_layer.b
curr_layer.output_val = self.actFun(curr_layer.input_val,
self.net_struct.active_fun_list[i - 1]) def backward(self):
'''反向'''
layer_num = len(self.net_struct.layers)
last_layer = self.net_struct.layers[layer_num - 1]
last_layer.error = -self.actFunGrad(last_layer.input_val,
self.net_struct.active_fun_list[layer_num - 2])
layer_index = list(range(1, layer_num - 1))
layer_index.reverse()
for i in layer_index:
curr_layer = self.net_struct.layers[i]
curr_layer.error = (last_layer.w.transpose().dot(last_layer.error)) * self.actFunGrad(curr_layer.input_val,self.net_struct.active_fun_list[i - 1])
last_layer = curr_layer def parDeriv(self):
'''标准梯度（求导）'''
layer_num = len(self.net_struct.layers)
for i in range(1, layer_num):
befor_layer = self.net_struct.layers[i - 1]
befor_input_val = befor_layer.output_val.transpose()
curr_layer = self.net_struct.layers[i]
curr_error = curr_layer.error
curr_error = curr_error.reshape(curr_error.shape[0]*curr_error.shape[1], 1, order='F')
row = curr_error.shape[0]
col = befor_input_val.shape[1]
a = np.zeros((row, col))
num = befor_input_val.shape[0]
neure_number = curr_layer.neure_number
for i in range(0, num):
a[neure_number*i:neure_number*i + neure_number,:] = np.repeat([befor_input_val[i,:]],neure_number,axis = 0)
tmp_w_par_deriv = curr_error * a
curr_layer.w_par_deriv = np.zeros((num, befor_layer.neure_number * curr_layer.neure_number))
for i in range(0, num):
tmp = tmp_w_par_deriv[neure_number*i:neure_number*i + neure_number,:]
tmp = tmp.reshape(tmp.shape[0] * tmp.shape[1], order='C')
curr_layer.w_par_deriv[i, :] = tmp
curr_layer.b_par_deriv = curr_layer.error.transpose() def jacobian(self):
'''雅可比行列式'''
layers = self.net_struct.neurals
row = self.net_struct.x.shape[1]
col = 0
for i in range(0, len(layers) - 1):
col = col + layers[i] * layers[i + 1] + layers[i + 1]
j = np.zeros((row, col))
layer_num = len(self.net_struct.layers)
index = 0
for i in range(1, layer_num):
curr_layer = self.net_struct.layers[i]
w_col = curr_layer.w_par_deriv.shape[1]
b_col = curr_layer.b_par_deriv.shape[1]
j[:, index : index + w_col] = curr_layer.w_par_deriv
index = index + w_col
j[:, index : index + b_col] = curr_layer.b_par_deriv
index = index + b_col
return j def gradCheck(self):
'''梯度检查'''
W1 = self.net_struct.layers[1].w
b1 = self.net_struct.layers[1].b
n = self.net_struct.layers[1].neure_number
W2 = self.net_struct.layers[2].w
b2 = self.net_struct.layers[2].b
x = self.net_struct.x
p = []
p.extend(W1.reshape(1,W1.shape[0]*W1.shape[1],order = 'C')[0])
p.extend(b1.reshape(1,b1.shape[0]*b1.shape[1],order = 'C')[0])
p.extend(W2.reshape(1,W2.shape[0]*W2.shape[1],order = 'C')[0])
p.extend(b2.reshape(1,b2.shape[0]*b2.shape[1],order = 'C')[0])
old_p = p
jac = []
for i in range(0, x.shape[1]):
xi = np.array([x[:,i]])
xi = xi.transpose()
ji = []
for j in range(0, len(p)):
W1 = np.array(p[0:2*n]).reshape(n,2,order='C')
b1 = np.array(p[2*n:2*n+n]).reshape(n,1,order='C')
W2 = np.array(p[3*n:4*n]).reshape(1,n,order='C')
b2 = np.array(p[4*n:4*n+1]).reshape(1,1,order='C') z2 = W1.dot(xi) + b1
a2 = self.actFun(z2)
z3 = W2.dot(a2) + b2
h1 = self.actFun(z3)
p[j] = p[j] + 0.00001
W1 = np.array(p[0:2*n]).reshape(n,2,order='C')
b1 = np.array(p[2*n:2*n+n]).reshape(n,1,order='C')
W2 = np.array(p[3*n:4*n]).reshape(1,n,order='C')
b2 = np.array(p[4*n:4*n+1]).reshape(1,1,order='C') z2 = W1.dot(xi) + b1
a2 = self.actFun(z2)
z3 = W2.dot(a2) + b2
h = self.actFun(z3)
g = (h[0][0]-h1[0][0])/0.00001
ji.append(g)
jac.append(ji)
p = old_p
return jac def jjje(self):
'''计算jj与je'''
layer_num = len(self.net_struct.layers)
e = self.net_struct.y - self.net_struct.layers[layer_num - 1].output_val
e = e.transpose()
j = self.jacobian()
#check gradient
#j1 = -np.array(self.gradCheck())
#jk = j.reshape(1,j.shape[0]*j.shape[1])
#jk1 = j1.reshape(1,j1.shape[0]*j1.shape[1])
#plt.plot(jk[0])
#plt.plot(jk1[0],'.')
#plt.show()
jj = j.transpose().dot(j)
je = -j.transpose().dot(e)
return[jj, je] def lm(self):
'''Levenberg-Marquardt训练算法'''
mu = self.mu
beta = self.beta
iteration = self.iteration
tol = self.tol
y = self.net_struct.y
layer_num = len(self.net_struct.layers)
self.forward()
pred = self.net_struct.layers[layer_num - 1].output_val
pref = self.perfermance(y, pred)
for i in range(0, iteration):
print('iter:',i, 'error:', pref)
#1) 第一步:
if(pref < tol):
break
#2) 第二步:
self.backward()
self.parDeriv()
[jj, je] = self.jjje()
while(1):
#3) 第三步:
A = jj + mu * np.diag(np.ones(jj.shape[0]))
delta_w_b = pinv(A).dot(je)
#4) 第四步:
old_net_struct = copy.deepcopy(self.net_struct)
self.updataNetStruct(delta_w_b)
self.forward()
pred1 = self.net_struct.layers[layer_num - 1].output_val
pref1 = self.perfermance(y, pred1)
if (pref1 < pref):
mu = mu / beta
pref = pref1
break
mu = mu * beta
self.net_struct = copy.deepcopy(old_net_struct) def updataNetStruct(self, delta_w_b):
'''更新网络权重及阈值'''
layer_num = len(self.net_struct.layers)
index = 0
for i in range(1, layer_num):
before_layer = self.net_struct.layers[i - 1]
curr_layer = self.net_struct.layers[i]
w_num = before_layer.neure_number * curr_layer.neure_number
b_num = curr_layer.neure_number
w = delta_w_b[index : index + w_num]
w = w.reshape(curr_layer.neure_number, before_layer.neure_number, order='C')
index = index + w_num
b = delta_w_b[index : index + b_num]
index = index + b_num
curr_layer.w += w
curr_layer.b += b def perfermance(self, y, pred):
'''性能函数'''
error = y - pred
return norm(error) / len(y) # 以下函数为测试样例
def plotSamples(n = 40):
x = np.array([np.linspace(0, 3, n)])
x = x.repeat(n, axis = 0)
y = x.transpose()
z = np.zeros((n, n))
for i in range(0, x.shape[0]):
for j in range(0, x.shape[1]):
z[i][j] = sampleFun(x[i][j], y[i][j])
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(x, y, z, cmap='autumn', cstride=2, rstride=2)
ax.set_xlabel("X-Label")
ax.set_ylabel("Y-Label")
ax.set_zlabel("Z-Label")
plt.show() def sinSamples(n):
x = np.array([np.linspace(-0.5, 0.5, n)])
#x = x.repeat(n, axis = 0)
y = x + 0.2
z = np.zeros((n, 1))
for i in range(0, x.shape[1]):
z[i] = np.sin(x[0][i] * y[0][i])
X = np.zeros((n, 2))
n = 0
for xi, yi in zip(x.transpose(), y.transpose()):
X[n][0] = xi
X[n][1] = yi
n = n + 1
# print(x.shape, y.shape)
# print(X.shape, z.shape)
return X, z.transpose() def peaksSamples(n):
x = np.array([np.linspace(-3, 3, n)])
x = x.repeat(n, axis = 0)
y = x.transpose()
z = np.zeros((n, n))
for i in range(0, x.shape[0]):
for j in range(0, x.shape[1]):
z[i][j] = sampleFun(x[i][j], y[i][j])
X = np.zeros((n*n, 2))
x_list = x.reshape(n*n,1 )
y_list = y.reshape(n*n,1)
z_list = z.reshape(n*n,1)
n = 0
for xi, yi in zip(x_list, y_list):
X[n][0] = xi
X[n][1] = yi
n = n + 1
# print(x.shape, y.shape)
# print(X.shape, z.shape, z_list.shape, z_list.transpose().shape)
return X,z_list.transpose() def sampleFun( x, y):
z = 3*pow((1-x),2) * exp(-(pow(x,2)) - pow((y+1),2)) - 10*(x/5 - pow(x, 3) - pow(y, 5)) * exp(-pow(x, 2) - pow(y, 2)) - 1/3*exp(-pow((x+1), 2) - pow(y, 2))
return z # 测试
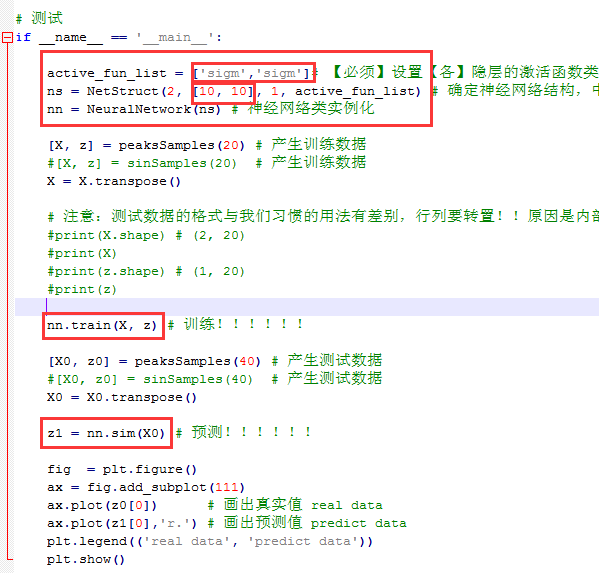
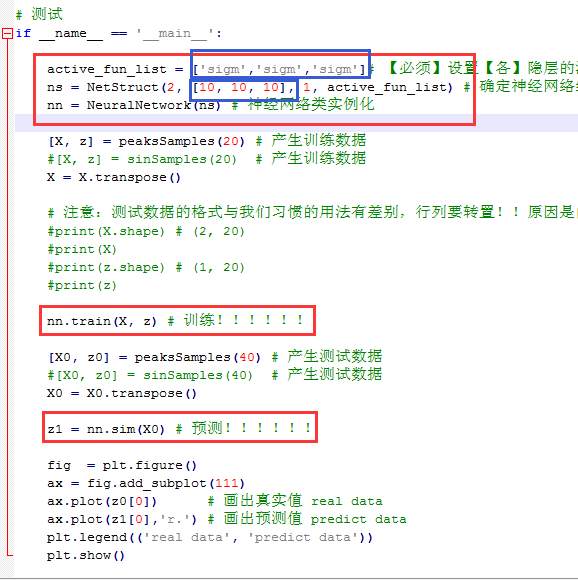
if __name__ == '__main__': active_fun_list = ['sigm','sigm','sigm']# 【必须】设置【各】隐层的激活函数类型，可以设置为tanh,radb，tanh,line类型，如果不显式的设置最后一层为line
ns = NetStruct(2, [10, 10, 10], 1, active_fun_list) # 确定神经网络结构，中间两个隐层各10个神经元
nn = NeuralNetwork(ns) # 神经网络类实例化 [X, z] = peaksSamples(20) # 产生训练数据
#[X, z] = sinSamples(20) # 第二个训练数据
X = X.transpose() # 注意：测试数据的格式与我们习惯的用法有差别，行列要转置！！原因是内部逻辑采用了矩阵运算？！！！！
#print(X.shape) # (2, 20)
#print(X)
#print(z.shape) # (1, 20)
#print(z) nn.train(X, z) # 训练！！！！！！ [X0, z0] = peaksSamples(40) # 产生测试数据
#[X0, z0] = sinSamples(40) # 第二个测试数据
X0 = X0.transpose() z1 = nn.sim(X0) # 预测！！！！！！ fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(z0[0]) # 画出真实值 real data
ax.plot(z1[0],'r.') # 画出预测值 predict data
plt.legend(('real data', 'predict data'))
plt.show()
可变多隐层神经网络的python实现的更多相关文章
- 实现一个单隐层神经网络python
看过首席科学家NG的深度学习公开课很久了,一直没有时间做课后编程题,做完想把思路总结下来,仅仅记录编程主线. 一 引用工具包 import numpy as np import matplotlib. ...
- 用C实现单隐层神经网络的训练和预测（手写BP算法）
实验要求:•实现10以内的非负双精度浮点数加法,例如输入4.99和5.70,能够预测输出为10.69•使用Gprof测试代码热度 代码框架•随机初始化1000对数值在0~10之间的浮点数,保存在二维数 ...
- Andrew Ng - 深度学习工程师 - Part 1. 神经网络和深度学习（Week 3. 浅层神经网络）
=================第3周 浅层神经网络=============== ===3..1 神经网络概览=== ===3.2 神经网络表示=== ===3.3 计算神经网络的输出== ...
- tensorflow-LSTM-网络输出与多隐层节点
本文从tensorflow的代码层面理解LSTM. 看本文之前,需要先看我的这两篇博客 https://www.cnblogs.com/yanshw/p/10495745.html 谈到网络结构 ht ...
- 1.4激活函数-带隐层的神经网络tf实战
激活函数 激活函数----日常不能用线性方程所概括的东西 左图是线性方程,右图是非线性方程 当男生增加到一定程度的时候,喜欢女生的数量不可能无限制增加,更加趋于平稳 在线性基础上套了一个激活函数,使得 ...
- 神经网络结构设计指导原则——输入层：神经元个数=feature维度 输出层：神经元个数=分类类别数，默认只用一个隐层 如果用多个隐层，则每个隐层的神经元数目都一样
神经网络结构设计指导原则 原文 http://blog.csdn.net/ybdesire/article/details/52821185 下面这个神经网络结构设计指导原则是Andrew N ...
- Neural Networks and Deep Learning（week3）Planar data classification with one hidden layer(基于单隐藏层神经网络的平面数据分类)
Planar data classification with one hidden layer 你会学习到如何: 用单隐层实现一个二分类神经网络 使用一个非线性激励函数,如 tanh 计算交叉熵的损 ...
- BP神经网络在python下的自主搭建梳理
本实验使用mnist数据集完成手写数字识别的测试.识别正确率认为是95% 完整代码如下: #!/usr/bin/env python # coding: utf-8 # In[1]: import n ...
- 吴恩达《深度学习》-第一门课 (Neural Networks and Deep Learning)-第三周：浅层神经网络(Shallow neural networks) -课程笔记
第三周:浅层神经网络(Shallow neural networks) 3.1 神经网络概述(Neural Network Overview) 使用符号$ ^{[
随机推荐
- 如何在定制化组件中实现并使用v-model
https://alligator.io/vuejs/add-v-model-support/
- MySQL binlog格式解析
MySQL binlog格式解析 binlog想必大家都不陌生,在主从复制或者某些情况下的数据恢复会用到.由于binlog是二进制数据,要查看一般都借助mysqlbinlog工具.这篇笔记分析了b ...
- OpenGLES渲染
OpenGLES渲染 OpenGLES使用GPU渲染图片,不占用CPU,但其使用还是挺复杂的. 先用OpenGLES显示一张图片: // // ShowViewController.m // Open ...
- Exchange & Office 365最小混合部署
前言 这篇文章的主题是混合部署~ 混合使得本地组织和云环境像一个单一的.协作紧密的组织一样运作.当组织决定进行混合部署,达到本地Exchange Server和Office 365共存的状态时,就会面 ...
- SpringMVC框架项目在编译运行是常见错误
1.问题描述(Spring_shizhan4ban_Chapter05应用):在自动注入FileValidator对象引用类型时报错,由于FileValidator是实体类,没有实现接口. @Auto ...
- Hadoop HBase概念学习系列之HBase里的Client（二十二）
这个,很简单,但凡是略懂大数据的,就很清楚,不多说,直接上图.
- 移动端上下滑动事件之--坑爹的touch.js
下面的方法,不知道是操作方法不对还是啥. 在 zepto.js 里面加那一段代码不起作用 百度的 touch.js 是可以用的,但是使用方式 和 zepto有点不一样. 解决方案:参照这个链接地址 ...
- python第二十课——math模块中常用的函数
属性: e:自然数 pi:圆周率 函数: ceil():向上取整 floor():向下取整 sqrt():开平方根 radians():角度转弧度 degrees():弧度转角度 import mat ...
- HDU5343:MZL's Circle Zhou(SAM,记忆化搜索DP)
Description Input Output Sample Input Sample Output Solution 题意:给你两个串,分别从两个里面各选出一个子串拼到一起,问能构成多少个本质不同 ...
- 【openjudge】【字符串+模拟】1777:文件结构“图”
[题目传送门:]戳 [描述:] 在计算机上看到文件系统的结构通常很有用.Microsoft Windows上面的"explorer"程序就是这样的一个例子.但是在有图形界面之前,没 ...