Gumbel-Softmax Trick和Gumbel分布

  之前看MADDPG论文的时候，作者提到在离散的信息交流环境中，使用了Gumbel-Softmax estimator。于是去搜了一下，发现该技巧应用甚广，如深度学习中的各种GAN、强化学习中的A2C和MADDPG算法等等。只要涉及在离散分布上运用重参数技巧时(re-parameterization)，都可以试试Gumbel-Softmax Trick。


  这篇文章是学习以下链接之后的个人理解，内容也基本出于此，需要深入理解的可以自取。

• The Humble Gumbel Distribution
• The Gumbel-Max Trick for Discrete Distributions
• The Gumbel-Softmax Trick for Inference of Discrete Variables
• 如何理解Gumbel-Max trick？

  这篇文章从直观感觉讲起，先讲Gumbel-Softmax Trick用在哪里及如何运用，再编程感受Gumbel分布的效果，最后讨论数学证明。

目录

• 一、Gumbel-Softmax Trick用在哪里
  • 问题来源
  • Re-parameterization Trick
  • Gumbel-Softmax Trick
• 二、Gumbel分布采样效果
• 三、数学证明

一、Gumbel-Softmax Trick用在哪里

问题来源

  通常在强化学习中，如果动作空间是离散的，比如上、下、左、右四个动作，通常的做法是网络输出一个四维的one-hot向量(不考虑空动作)，分别代表四个动作。比如[1,0,0,0]代表上，[0,1,0,0]代表下等等。而具体取哪个动作呢，就根据输出的每个维度的大小，选择值最大的作为输出动作,即\(\arg\max(v)\)。


  例如网络输出的四维向量为\(v=[-20,10,9.6,6.2]\)，第二个维度取到最大值10，那么输出的动作就是[0,1,0,0]，也就是下，这和多类别的分类任务是一个道理。但是这种取法有个问题是不能计算梯度，也就不能更新网络。通常的做法是加softmax函数，把向量归一化，这样既能计算梯度，同时值的大小还能表示概率的含义。softmax函数定义如下：

\[\sigma(z_i)=\frac{e^{z_i}}{\sum\limits_{j=1}^Ke^{z_j}}
\]

  那么将\(v=[-20,10,9.6,6.2]\)通过softmax函数后有\(\sigma(v)=[0,0.591,0.396,0.013]\)，这样做不会改变动作或者说类别的选取，同时softmax倾向于让最大值的概率显著大于其他值，比如这里10和9.6经过softmax放缩之后变成了0.591和0.396，6.2对应的概率更是变成了0.013，这有利于把网络训成一个one-hot输出的形式，这种方式在分类问题中是常用方法。


  但是这么做还有一个问题，这个表示概率的向量\(\sigma(v)=[0,0.591,0.396,0.013]\)并没有真正显示出概率的含义，因为一旦某个值最大，就选择相应的动作或者分类。比如\(\sigma(v)=[0,0.591,0.396,0.013]\)和\(\sigma(v)=[0,0.9,0.1,0]\)在类别选取的结果看来没有任何差别，都是选择第二个类别，但是从概率意义上讲差别是巨大的。所以需要一种方法不仅选出动作，而且遵从概率的含义。


  很直接的方法是依概率采样就完事了，比如直接用np.random.choice函数依照概率生成样本值，这样概率就有意义了。这样做确实可以，但是又有一个问题冒了出来：这种方式怎么计算梯度？不能计算梯度怎么用BP的方式更新网络？


  这时重参数(re-parameterization)技巧解决了这个问题，这里有详尽的解释，不过比较晦涩。简单来说重参数技巧的一个用处是把采样的步骤移出计算图，这样整个图就可以计算梯度BP更新了。之前我一直在想分类任务直接softmax之后BP更新不就完事了吗，为什么非得采样。后来看了VAE和GAN之后明白，还有很多需要采样训练的任务。这里举简单的VAE(变分自编码器)的例子说明需要采样训练的任务以及重参数技巧，详细内容来自视频和博客。

Re-parameterization Trick

  最原始的自编码器通常长这样：





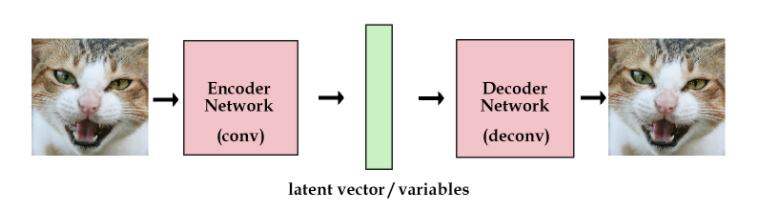
  左右两边是端到端的出入输出网络，中间的绿色是提取的特征向量，这是一种直接从图片提取特征的方式。
  而VAE长这样:





  VAE的想法是不直接用网络去提取特征向量，而是提取这张图像的分布特征，也就把绿色的特征向量替换为分布的参数向量，比如说均值和标准差。然后需要decode图像的时候，就从encode出来的分布中采样得到特征向量样本，用这个样本去重建图像，这时怎么计算梯度的问题就出现了。
  重参数技巧可以解决这个问题，它长下面这样:





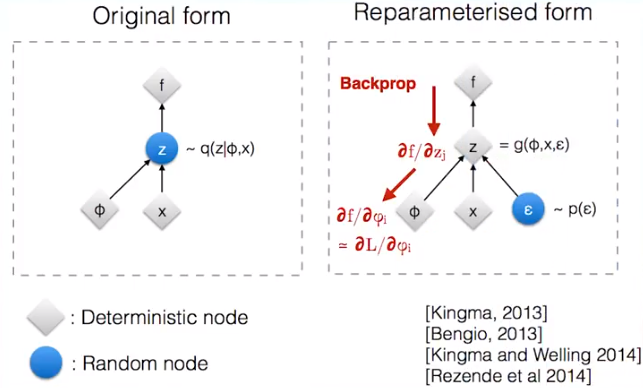
  假设图中的\(x\)和\(\phi\)表示VAE中的均值和标准差向量，它们是确定性的节点。而需要输出的样本\(z\)是带有随机性的节点，重参数就是把带有随机性的\(z\)变成确定性的节点，同时随机性用另一个输入节点\(\epsilon\)代替。例如，这里用正态分布采样，原本从均值为\(x\)和标准差为\(\phi\)的正态分布\(N(x,\phi^2)\)中采样得到\(z\)。将其转化成从标准正态分布\(N(0,1)\)中采样得到\(\epsilon\),再计算得到\(z=x+\epsilon\cdot \phi\)。这样一来，采样的过程移出了计算图，整张计算图就可以计算梯度进行更新了，而新加的\(\epsilon\)的输入分支不做更新，只当成一个没有权重变化的输入。


  到这里，需要采样训练的任务实例以及重参数技巧基本有个概念了。

Gumbel-Softmax Trick

  VAE的例子是一个连续分布(正态分布)的重参数，离散分布的情况也一样，首先需要可以采样，使得离散的概率分布有意义而不是只取概率最大的值，其次需要可以计算梯度。那么怎么做到的，具体操作如下：


  对于\(n\)维概率向量\(\pi\),对\(\pi\)对应的离散随机变量\(x_{\pi}\)添加Gumbel噪声，再取样

\[x_{\pi}=\arg\max(\log(\pi_i)+G_i)
\]

  其中，\(G_i\)是独立同分布的标准Gumbel分布的随机变量，标准Gumbel分布的CDF为\(F(x)=e^{-e^{-x}}\)。
  这就是Gumbel-Max trick。可以看到由于这中间有一个\(\arg\max\)操作，这是不可导的，所以用softmax函数代替之，也就是Gumbel-Softmax Trick，而\(G_i\)可以通过Gumbel分布求逆从均匀分布生成，即\(G_i=-\log(-\log(U_i)),U_i\sim U(0,1)\),这样就搞定了。


  具体实践是这样操作的,

• 对于网络输出的一个\(n\)维向量\(v\),生成\(n\)个服从均匀分布\(U(0,1)\)的独立样本\(\epsilon_1,...,\epsilon_n\)
  
• 通过\(G_i=-\log(-\log(\epsilon_i))\)计算得到\(G_i\)
  
• 对应相加得到新的值向量\(v'=[v_1+G_1,v_2+G_2,...,v_n+G_n]\)
  
• 通过softmax函数

\[\sigma_{\tau}(v'_i)=\frac{e^{v'_i/\tau}}{\sum\limits_{j=1}^ne^{v'_j/\tau}}
\]

  计算概率大小得到最终的类别。其中\(\tau\)是温度参数。


  直观上感觉，对于强化学习来说，在选择动作之前加一个扰动，相当于增加探索度，感觉上是合理的。对于深度学习的任务来说，添加随机性去模拟分布的样本生成，也是合情合理的。

二、Gumbel分布采样效果

  为什么使用Gumbel分布生成随机数，就能模拟离散概率分布的样本呢？这部分使用代码模拟来感受它的优越性。这部分例子和代码来自这里。


  首先Gumbel分布的概率密度函数长这样：

\[p(x)=\frac{1}{\beta}e^{-z-e^{-z}}
\]

  其中\(z=\frac{x-\mu}{\beta}\)。


  Gumbel分布是一类极值分布，那么它表示什么含义呢？原链接举了一个ice cream的例子，没有get到点。这里举一个类似的喝水的例子。

  比如你每天都会喝很多次水(比如100次)，每次喝水的量也不一样。假设每次喝水的量服从正态分布\(N(\mu,\sigma^2)\)(其实也有点不合理，毕竟喝水的多少不能取为负值，不过无伤大雅能理解就好，假设均值为5)，那么每天100次喝水里总会有一个最大值，这个最大值服从的分布就是Gumbel分布。实际上，只要是指数族分布，它的极值分布都服从Gumbel分布。那么上面这个例子的分布长什么样子呢，作图有

from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt
mean_hunger = 5
samples_per_day = 100
n_days = 10000
samples = np.random.normal(loc=mean_hunger, size=(n_days, samples_per_day))
daily_maxes = np.max(samples, axis=1)

def gumbel_pdf(prob,loc,scale):
    z = (prob-loc)/scale
    return np.exp(-z-np.exp(-z))/scale

def plot_maxes(daily_maxes):
    probs,hungers,_=plt.hist(daily_maxes,density=True,bins=100)
    plt.xlabel('Volume')
    plt.ylabel('Probability of Volume being daily maximum')
    (loc,scale),_=curve_fit(gumbel_pdf,hungers[:-1],probs)
    #curve_fit用于曲线拟合
    #接受需要拟合的函数（函数的第一个参数是输入，后面的是要拟合的函数的参数）、输入数据、输出数据
    #返回的是函数需要拟合的参数
    # https://blog.csdn.net/guduruyu/article/details/70313176
    plt.plot(hungers,gumbel_pdf(hungers,loc,scale))

plt.figure()
plot_maxes(daily_maxes)

  那么gumbel分布在离散分布的采样中效果如何呢？可以作图比较一下。先定义一个多项分布，作出真实的概率密度图。再通过采样的方式比较各种方法的效果。


  如下代码定义了一个7类别的多项分布，其真实的密度函数如下图

n_cats = 7
cats = np.arange(n_cats)
probs = np.random.randint(low=1, high=20, size=n_cats)
probs = probs / sum(probs)
logits = np.log(probs)
def plot_probs():
    plt.bar(cats, probs)
    plt.xlabel("Category")
    plt.ylabel("Probability")
plt.figure()
plot_probs()

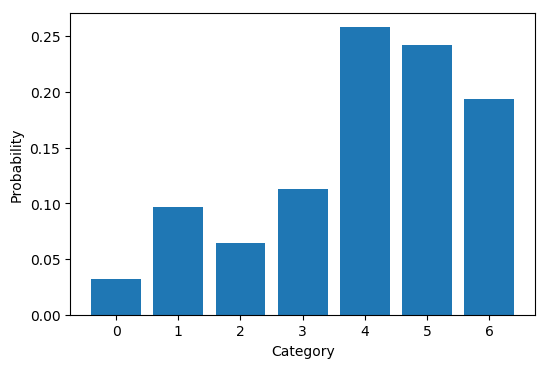
  首先我们直接根据真实的分布利用np.random.choice函数采样对比效果

n_samples = 1000
def plot_estimated_probs(samples,ylabel=''):
    n_cats = np.max(samples)+1
    estd_probs,_,_ = plt.hist(samples,bins=np.arange(n_cats+1),align='left',edgecolor='white',density=True)
    plt.xlabel('Category')
    plt.ylabel(ylabel+'Estimated probability')
    return estd_probs
def print_probs(probs):
    print('  '.join(['{:.2f}']`len(probs)).format(`probs))

samples = np.random.choice(cats,p=probs,size=n_samples) 

plt.figure()
plt.subplot(1,2,1)
plot_probs()
plt.subplot(1,2,2)
estd_probs = plot_estimated_probs(samples)
plt.tight_layout()#紧凑显示图片

print('Original probabilities:\t\t',end='')
print_probs(probs)
print('Estimated probabilities:\t',end='')
print_probs(estd_probs)

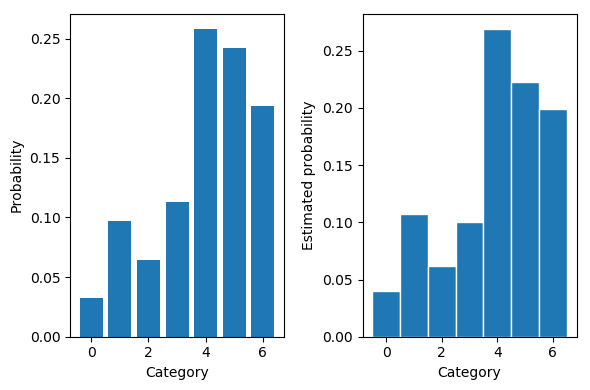
Original probabilities:  0.11 0.05 0.12 0.21 0.12 0.26 0.14

Estimated probabilities: 0.12 0.04 0.12 0.23 0.10 0.26 0.13


  效果意料之中的好。可以想到要是没有不能求梯度这个问题，直接从原分布采样是再好不过的。


  接着通过前述的方法添加Gumbel噪声采样，同时也添加正态分布和均匀分布的噪声作对比

def sample_gumbel(logits):
    noise = np.random.gumbel(size=len(logits))
    sample = np.argmax(logits+noise)
    return sample
gumbel_samples = [sample_gumbel(logits) for _ in range(n_samples)]

def sample_uniform(logits):
    noise = np.random.uniform(size=len(logits))
    sample = np.argmax(logits+noise)
    return sample
uniform_samples = [sample_uniform(logits) for _ in range(n_samples)]

def sample_normal(logits):
    noise = np.random.normal(size=len(logits))
    sample = np.argmax(logits+noise)
    return sample
normal_samples = [sample_normal(logits) for _ in range(n_samples)]

plt.figure(figsize=(10,4))
plt.subplot(1,4,1)
plot_probs()
plt.subplot(1,4,2)
gumbel_estd_probs = plot_estimated_probs(gumbel_samples,'Gumbel ')
plt.subplot(1,4,3)
normal_estd_probs = plot_estimated_probs(normal_samples,'Normal ')
plt.subplot(1,4,4)
uniform_estd_probs = plot_estimated_probs(uniform_samples,'Uniform ')
plt.tight_layout()

print('Original probabilities:\t\t',end='')
print_probs(probs)
print('Gumbel Estimated probabilities:\t',end='')
print_probs(gumbel_estd_probs)
print('Normal Estimated probabilities:\t',end='')
print_probs(normal_estd_probs)
print('Uniform Estimated probabilities:',end='')
print_probs(uniform_estd_probs)

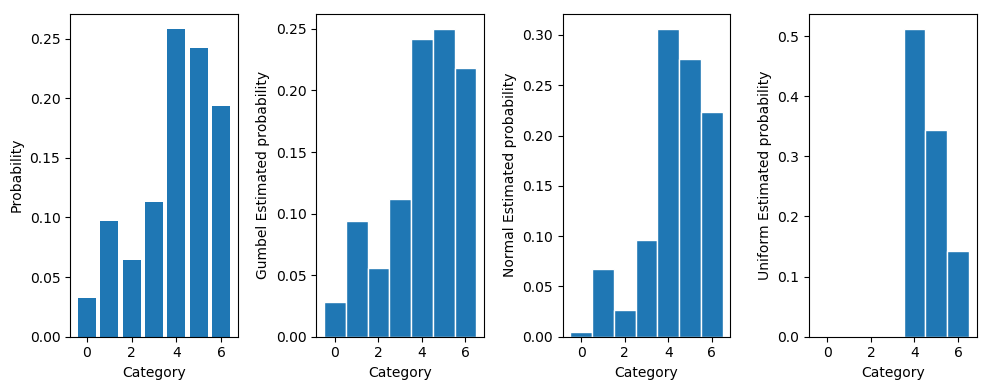
Original probabilities:      0.11 0.05 0.12 0.21 0.12 0.26 0.14

Gumbel Estimated probabilities: 0.11 0.04 0.11 0.23 0.12 0.26 0.14

Normal Estimated probabilities:  0.08 0.02 0.11 0.26 0.11 0.29 0.12

Uniform Estimated probabilities: 0.00 0.00 0.00 0.32 0.01 0.63 0.03


  可以明显看到Gumbel噪声的采样效果是最好的，正态分布其次，均匀分布最差。也就是说可以用Gumbel分布做Re-parameterization使得整个图计算可导，同时样本点最接近真实分布的样本。

三、数学证明

  为什么添加Gumbel噪声有如此效果，下面阐述问题并给出证明。


  假设有一个\(K\)维的输出向量，每个维度的值记为\(x_k\),通过softmax函数可得，取到每个维度的概率为：

\[\pi_k=\frac{e^{x_k}}{\sum^K_{k'=1}e^{x'_k}}
\]

  这是直接softmax得到的概率密度函数，如果换一种方式，对每个\(x_k\)添加独立的标准Gumbel分布(尺度参数为1，位置参数为0)噪声，并选择值最大的维度作为输出，得到的概率密度同样为\(\pi_k\)。


  下面给出Gumbel分布的概率密度函数和分布函数，并证明这件事情。

  尺度参数为1，位置参数为\(\mu\)的Gumbel分布的PDF为

\[f(z;\mu)=e^{-(z-\mu)-e^{-(z-\mu)}}
\]

  CDF为

\[F(z;\mu)=e^{-e^{-(z-\mu)}}
\]

  假设第\(k\)个Gumbel分布对应\(x_k\),加和得到随机变量\(z_k=x_k+G_k\),即相当于\(z_k\)服从尺度参数为1，位置参数为\(\mu=x_k\)的Gumbel分布。要证明这样取得的随机变量\(z_k\)与原随机变量相同，只需证明取到\(z_k\)的概率为\(\pi_k\)。也就是\(z_k\)比其他所有\(z_{k'}(k'\not=k)\)大的概率为\(\pi_k\)，即

\[P(z_k\ge z_{k'};\forall k'\not = k|\{x_{k'}\}_{k'=1}^K)=\pi_k
\]

  关于\(z_k\)的条件累积概率分布函数为

\[P(z_k\ge z_{k'};\forall k'\not = k|z_k,\{x_{k'}\}_{k'=1}^K)=P(z_1\le z_k)P(z_2\le z_k)\cdot\cdot\cdot P(z_{k-1}\le z_{k})P(z_{k+1}\le z_{k})\cdot\cdot\cdot P(z_K\le z_k)
\]

  即

\[P(z_k\ge z_{k'};\forall k'\not = k|z_k,\{x_{k'}\}_{k'=1}^K)=\prod\limits_{k'\not= k}e^{-e^{-(z_k-x_{k'})}}
\]

  对\(z_k\)求积分可得边缘累积概率分布函数

\[P(z_k\ge z_{k'};\forall k'\not = k|\{x_{k'}\}_{k'=1}^K)=\int P(z_k\ge z_{k'};\forall k'\not = k|z_k,\{x_{k'}\}_{k'=1}^K)\cdot f(z_k;x_k)\,dz_k
\]

  带入式子有

\[P(z_k\ge z_{k'};\forall k'\not = k|\{x_{k'}\}_{k'=1}^K)=\int \prod\limits_{k'\not= k}e^{-e^{-(z_k-x_{k'})}}\cdot e^{-(z_k-x_k)-e^{-(z_k-x_k)}}\,dz_k
\]

  化简有

\[\begin{array}{l}
P(z_k\ge z_{k'};\forall k'\not = k|\{x_{k'}\}_{k'=1}^K)\\ \qquad \qquad =\int \prod_{k'\not= k}e^{-e^{-(z_k-x_{k'})}}\cdot e^{-(z_k-x_k)-e^{-(z_k-x_k)}}\,dz_k \\
\qquad \qquad = \int e^{-\sum_{k'\not=k}e^{-(z_k-x_{k'})}-(z_k-x_k)-e^{-(z_k-x_k)}}\,dz_k\\
\qquad \qquad = \int e^{-\sum_{k'=1}^Ke^{-(z_k-x_{k'})}-(z_k-x_k)}\,dz_k\\
\qquad \qquad = \int e^{-(\sum_{k'=1}^Ke^{x_{k'}})e^{-z_k}-z_k+x_k}\,dz_k\\
\qquad \qquad = \int e^{-e^{-z_k+\ln(\sum_{k'=1}^Ke^{x_{k'}})}-z_k+x_k}\,dz_k \\
\qquad \qquad = \int e^{-e^{-(z_k-\ln(\sum_{k'=1}^Ke^{x_{k'}}))}-(z_k-\ln(\sum_{k'=1}^Ke^{x_{k'}}))-\ln(\sum_{k'=1}^Ke^{x_{k'}})+x_k}\,dz_k \\
\qquad \qquad = e^{-\ln(\sum_{k'=1}^Ke^{x_{k'}})+x_k}\int e^{-e^{-(z_k-\ln(\sum_{k'=1}^Ke^{x_{k'}}))}-(z_k-\ln(\sum_{k'=1}^Ke^{x_{k'}}))}\,dz_k\\
\qquad \qquad = \frac{e^{x_k}}{\sum_{k'=1}^Ke^{x_{k'}}}\int e^{-e^{-(z_k-\ln(\sum_{k'=1}^Ke^{x_{k'}}))}-(z_k-\ln(\sum_{k'=1}^Ke^{x_{k'}}))}\,dz_k \\
\qquad \qquad = \frac{e^{x_k}}{\sum_{k'=1}^Ke^{x_{k'}}}\int e^{-(z_k-\ln(\sum_{k'=1}^Ke^{x_{k'}}))-e^{-(z_k-\ln(\sum_{k'=1}^Ke^{x_{k'}}))}}\,dz_k
\end{array}
\]

  积分里面是\(\mu=\ln(\sum_{k'=1}^Ke^{x_{k'}})\)的Gumbel分布，所以整个积分为1。则有

\[P(z_k\ge z_{k'};\forall k'\not = k|\{x_{k'}\}_{k'=1}^K)=\frac{e^{x_k}}{\sum_{k'=1}^Ke^{x_{k'}}}
\]

  这和softmax的结果一致。