CF 1041 F. Ray in the tube

F. Ray in the tube

链接

题意：

　　有两条平行于x轴的直线A,B，每条直线上的某些位置有传感器。你需要确定A,B轴上任意两个整点位置$x_a$,$x_b$，使得一条光线沿$x_a→x_b$射出（碰到A,B后反射），能够碰到的传感器数量最多是多少。 每条直线上的传感器数量≤105，0≤xi≤10⁹ 

分析：

　　很有意思的一道题。

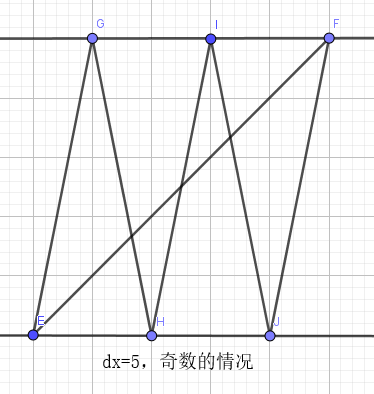
　　发现和y没什么关系，只要确定$x_a$,$x_b$之间的水平距离差dx就行了。

　　然后寻找性质：

　　1、如果dx为奇数，那么dx一定可以用1来代替，并且不会更差。

　　2、如果dx为偶数，那么dx一定可以用2的幂来代替，并且不会更差。

　　于是可以枚举dx，然后判断。复杂度$O(nlognlog(10^9))$

代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
#include<cctype>
#include<set>
#include<queue>
#include<vector>
#include<map>
using namespace std;
typedef long long LL;

inline int read() {
    int x=,f=;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-;
    for(;isdigit(ch);ch=getchar())x=x*+ch-'';return x*f;
}

const int N = ;
int A[N], B[N], C[N];

int main() {
    int n = read();read();
    for (int i = ; i <= n; ++i) A[i] = read();
    int m = read();read();
    for (int i = ; i <= m; ++i) B[i] = read();
    int ans = ; C[n + m + ] = 1e9 + ;
    for (int k = ; k <= ; k <<= ) {
        for (int i = ; i <= n; ++i) C[i] = A[i] % (k + k);
        for (int i = ; i <= m; ++i) C[i + n] = (B[i] + k) % (k + k);
        sort(C + , C + n + m + );
        for (int i = , pre = ; i <= n + m; ++i)
            if (C[i] != C[i + ]) ans = max(ans, i - pre + ), pre = i + ;
    }
    cout << ans;
    return ;
}