[agc008f] Black Radius 树形dp

Description

​ 给你一棵有NN个节点的树，节点编号为11到NN，所有边的长度都为11

​ "全"对某些节点情有独钟，这些他喜欢的节点的信息会以一个长度为NN的字符串ss的形式给到你，具体一点就是对于1<=i<=N1<=i<=N，si=1si=1表示"全"喜欢节点ii，为00表示"全"不喜欢节点ii

​ 一开始的时候，所有的节点都是白色的，"全"会进行以下操作恰好一次：

​ 选择一个他喜欢的节点vv和一个非负整数dd，然后将所有与节点vv距离不超过dd的节点全部涂黑

​ 问进行操作之后，有多少种不同的涂色情况？两种情况不同当且仅当两种情况存在一个节点ii的颜色不同

Input

​ 第一行一个正整数NN

​ 接下来N−1N−1行每行两个正整数xi,yixi,yi表示xixi到yiyi有一条边

​ 最后一行一个字符串ss

Output

​ 输出不同染色情况的数量

Sample Input

#Sample1
4
1 2
1 3
1 4
1100

#Sample2
5
1 2
1 3
1 4
4 5
11111

#Sample3
6
1 2
1 3
1 4
2 5
2 6
100011

Sample Output

#Sample1
4

#Sample2
11

#Sample3
8

HINT

​ 数据范围：

​ 对于100%的数据，2<=N<=2∗105,1<=xi,yi<=N2<=N<=2∗105,1<=xi,yi<=N,s由00或11构成，并且ss中最少有一个11

​ 样例解释：

​ Sample1：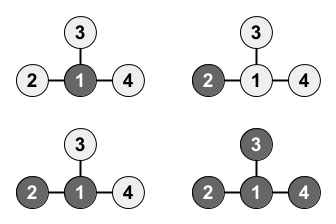

Sol

真的是神题，以下翻译的是官方题解。。。

orzCKW

Code

#include <bits/stdc++.h>
using namespace std;
vector<int>e[200005];char s[200005];long long ans;
int x,y,n,tot,cnt[200005],d1[200005],d2[200005],R[200005],L[200005];
int dfs1(int x,int fa)
{
    for(int i=0;i<e[x].size();i++) if(e[x][i]!=fa)
    {
        cnt[x]+=dfs1(e[x][i],x);
        if(d1[e[x][i]]+1>d1[x]) d2[x]=d1[x],d1[x]=d1[e[x][i]]+1;
        else if(d1[e[x][i]]+1>d2[x]) d2[x]=d1[e[x][i]]+1;
    }
    return cnt[x]+=s[x]-'0';
}
void dfs2(int x,int fa,int v)
{
    R[x]=v>d1[x]?d1[x]:max(v,d2[x]),L[x]=(s[x]-'0')?0:(tot-cnt[x]?v:1e9);
    if(fa)
    {
        if(d1[x]==v-1) ans++;
        else if(d1[x]<v-1) ans+=(cnt[x]>0);
        else ans+=(tot-cnt[x]>0);
    }
    for(int i=0;i<e[x].size();i++) if(e[x][i]!=fa)
    {
        if(cnt[e[x][i]]) L[x]=min(L[x],d1[e[x][i]]+1);
        if(d1[e[x][i]]+1==d1[x]) dfs2(e[x][i],x,max(v+1,d2[x]+1));
        else dfs2(e[x][i],x,max(v+1,d1[x]+1));
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<n;i++) scanf("%d%d",&x,&y),e[x].push_back(y),e[y].push_back(x);
    scanf("%s",s+1);
    for(int i=1;i<=n;i++) tot+=s[i]-'0';
    dfs1(1,0);dfs2(1,0,0);
    for(int i=1;i<=n;i++) if(L[i]<=R[i]) ans+=(R[i]-L[i]+1);
    printf("%lld\n",ans);
}