[hdu 6069]素数筛+区间质因数分解

给[L,R]区间的每一个数都质因数分解的复杂度可以达到(R-L)logR，真的涨姿势……

另外，质因数分解有很重要的一点，就是只需要打sqrt(R)以内的素数表就够了……因为超过sqrt(R)的至多只有一个，分解其他的那些剩下的就是了。

果然学习的过程中要精益求精，把时间和空间都尽量降到最低。

此外还有一个很重要的公式。d(i)表示i的因子个数。那么

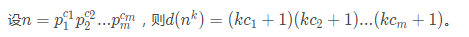
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int MAXN=;
int prime[MAXN+];
void getPrime()
{
    memset(prime,,sizeof(prime));
    for(int i=; i<=MAXN; i++)
    {
        if(!prime[i])prime[++prime[]]=i;
        for(int j=; j<=prime[]&&prime[j]<=MAXN/i; j++)
        {
            prime[prime[j]*i]=;
            if(i%prime[j]==) break;
        }
    }
}

const int md=;
long long sj[MAXN+];
long long fj[MAXN+];
long long k;

void getfact(long long l,long long r)
{
    for (long long i=l;i<=r;i++)
    {
        fj[i-l]=;
        sj[i-l]=i;
    }
    for (int i=;i<=prime[];i++)
    {
        long long th=prime[i];
        for (long long j=(l-)/th*th+th;j<=r;j+=th)
        {
            int cnt=;
            while (sj[j-l]%th==)
            {
                cnt++;
                sj[j-l]/=th;
            }
            fj[j-l]=fj[j-l]*(k*cnt%md+)%md;
        }
    }
    for (long long i=l;i<=r;i++)
    {
        if (sj[i-l]!=)
        {
            fj[i-l]=fj[i-l]*(k+)%md;
        }
    }
}

int main()
{
    getPrime();
    int t;
    scanf("%d",&t);
    while (t--)
    {
        ll l,r;
        scanf("%I64d%I64d%I64d",&l,&r,&k);
        getfact(l,r);
        long long ans=;
        for (long long i=l;i<=r;i++)
        {
            ans=(ans+fj[i-l])%md;
        }
        printf("%I64d\n",ans);
    }
    return ;
}