【CF MEMSQL 3.0 D. Third Month Insanity】

time limit per test 2 seconds

memory limit per test 256 megabytes

input standard input

output standard output

The annual college sports-ball tournament is approaching, which for trademark reasons we'll refer to as Third Month Insanity. There are a total of 2^N teams participating in the tournament, numbered from 1 to 2^N. The tournament lasts N rounds, with each round eliminating half the teams. The first round consists of 2^N - 1 games, numbered starting from 1. In game i, team 2·i - 1 will play against team 2·i. The loser is eliminated and the winner advances to the next round (there are no ties). Each subsequent round has half as many games as the previous round, and in game i the winner of the previous round's game 2·i - 1 will play against the winner of the previous round's game2·i.

Every year the office has a pool to see who can create the best bracket. A bracket is a set of winner predictions for every game. For games in the first round you may predict either team to win, but for games in later rounds the winner you predict must also be predicted as a winner in the previous round. Note that the bracket is fully constructed before any games are actually played. Correct predictions in the first round are worth 1 point, and correct predictions in each subsequent round are worth twice as many points as the previous, so correct predictions in the final game are worth 2^N - 1 points.

For every pair of teams in the league, you have estimated the probability of each team winning if they play against each other. Now you want to construct a bracket with the maximum possible expected score.

Input

Input will begin with a line containing N (2 ≤ N ≤ 6).

2^N lines follow, each with 2^N integers. The j-th column of the i-th row indicates the percentage chance that team i will defeat team j, unless i = j, in which case the value will be 0. It is guaranteed that the i-th column of the j-th row plus the j-th column of the i-th row will add to exactly 100.

Output

Print the maximum possible expected score over all possible brackets. Your answer must be correct to within an absolute or relative error of 10^- 9.

Formally, let your answer be a, and the jury's answer be b. Your answer will be considered correct, if .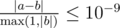

Examples

input

2
0 40 100 100
60 0 40 40
0 60 0 45
0 60 55 0

output

1.75

input

3
0 0 100 0 100 0 0 0
100 0 100 0 0 0 100 100
0 0 0 100 100 0 0 0
100 100 0 0 0 0 100 100
0 100 0 100 0 0 100 0
100 100 100 100 100 0 0 0
100 0 100 0 0 100 0 0
100 0 100 0 100 100 100 0

output

12

input

2
0 21 41 26
79 0 97 33
59 3 0 91
74 67 9 0

output

3.141592

Note

In the first example, you should predict teams 1 and 4 to win in round 1, and team 1 to win in round 2. Recall that the winner you predict in round 2 must also be predicted as a winner in round 1.

【翻译】2ⁿ个人参加比赛。相邻两个人决出胜负进入下一轮比赛(所以共有n轮)。输出p[i][j]表示i在比赛中战胜j的概率(p[j][i]=1-p[i][j])。每一轮你可以给两两对决的选手其中之一下赌注，如果该选手胜利那么将获得2^k的钱（k表示当前为第k轮）。求获得最优收益的期望值。

题解：
     ①期望动态规划。首先可以想到需要表示这一场比赛哪个人赢了。

     ②以dfs的形式降到最底层，g[i][j]表示二叉树节点i(代表了一个区间)上j成为最终胜利者的概率，f[i][j]表示上述状态下的最有收益期望值。

     ③g的转移即枚举j最后和哪些人对决并胜出。

     ④f的转移即j胜出的概率乘上收益并加上所有和j比赛的人中之前的最优期望收益值。

#include<stdio.h>
#include<algorithm>
#define go(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int N=1003;int k,n;
double p[N][N],f[N][N],g[N][N],ans;
void dfs(int u,int l,int r)
{
	if(l==r){f[u][l]=0;g[u][l]=1;return;}
	int M=l+r>>1;dfs(u<<1,l,M);dfs(u<<1|1,M+1,r);

	go(i,1,M)go(j,M+1,n)g[u][i]+=g[u<<1][i]*g[u<<1|1][j]*p[i][j];
	go(i,M+1,n)go(j,1,M)g[u][i]+=g[u<<1|1][i]*g[u<<1][j]*p[i][j];
	go(i,1,M)go(j,M+1,n)f[u][i]=max(f[u][i],g[u][i]*(r-l+1)/2+f[u<<1][i]+f[u<<1|1][j]);
	go(i,M+1,n)go(j,1,M)f[u][i]=max(f[u][i],g[u][i]*(r-l+1)/2+f[u<<1|1][i]+f[u<<1][j]);
}
int main()
{
	scanf("%d",&k);n=1<<k;
	go(i,1,n)go(j,1,n)scanf("%lf",&p[i][j]),p[i][j]/=100;
	dfs(1,1,n);go(i,1,n)ans=max(ans,f[1][i]);printf("%.10lf\n",ans);
	return 0;
}//Paul_Guderian