【BZOJ4657】tower [网络流]

炮塔

Time Limit: 10 Sec  Memory Limit: 256 MB

Description

　　

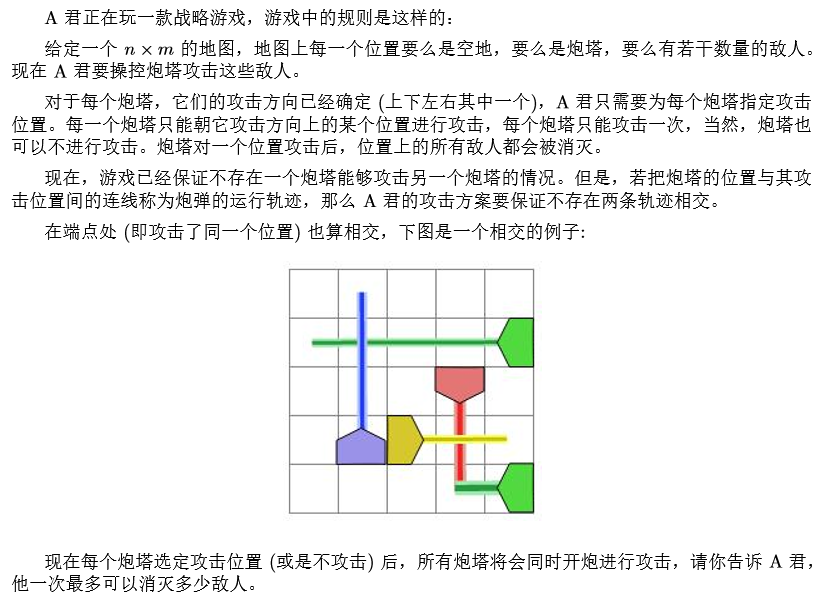
Input

　　

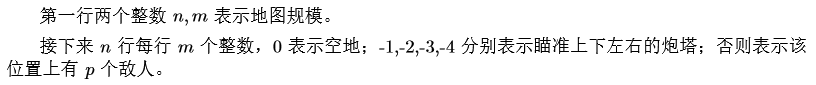
Output

　　一行一个整数表示答案。

Sample Input

　　4 5
　　0 0 -2 0 0
　　-4 0 5 4 0
　　0 -4 3 0 6
　　9 0 0 -1 0

Sample Output

　　12

HINT

　　

Main idea

　　给定若干固定方向的炮台，以及若干位置的敌人，炮台可以杀掉对应方向上从该位置到底的其中一个位置的敌人，要求炮台位置和消灭的敌人位置连线，连线不能有重叠，询问最多能消灭几个敌人。

Solution

　　我们发现，相交的连线其实就是给出了炮台之间的路径。我们来处理如何解决无可走路径的问题，显然想到了最小割。

　　横向炮台或纵向炮台之间是没有影响的。所以显然可以构建一张二分图。

　　那么我们如何确定容量呢？我们可以令一条 (u->v) 的割边表示选择了u这个点。方便处理连边上下或左右攻击的炮台，连边方向应该一致。然后我们连边时先找到一条可攻击位置上的最大贡献，设最大贡献为Max，然后连边时容量用Max-val，就表示它会损失这么多的价值。注意到这样连边的话，在最边界上的点是没有连边的。但是并不会影响答案，为什么呢？我们这么考虑：如果我们选择了最边界的点，那么这个位置的敌人数必然是最多的，如果不是最多的话（也就是说还有其它点人数更多）显然连到边界不可能是最优的，因为连边界就可能阻断了更多其它炮台攻击方案的可能性。这就表示了，若选择边界，则必然边界贡献最多，那么如果连边了，容量也应该是0，综上所述不会影响答案。

　　我们这样连完了边，但发现还是会有一些问题。如果出现这种情况，就会有一些Bug：

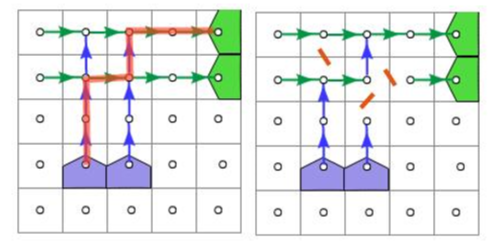
　　这样就会影响了答案。怎么处理呢？我们发现问题只能涉及一行一列，只要令路径只能“拐一次弯”就可以解决。所以我们可以再将点拆为横向点和纵向点，横向点向纵向点连INF的边，纵向点没有边连向横向点即可。

　　这样的话复杂度就是O(maxflow(n×m,n×m))，成功了解决了问题！\(≧▽≦)/

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;

 const int ONE = ;
 const int INF = ;

 int n,m;
 int S,T;
 int Ans;
 int a[][],Max;
 int next[ONE],first[ONE],go[ONE],w[ONE],tot;
 int q[],Dep[ONE],E[ONE],tou,wei;
 #define id(i,j) (i-1)*m+j

 int get()
 {
         int res,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 void Add(int u,int v,int z)
 {
         next[++tot]=first[u];    first[u]=tot;    go[tot]=v;    w[tot]=z;
         next[++tot]=first[v];    first[v]=tot;    go[tot]=u;    w[tot]=;
 }

 int Bfs()
 {
         memset(Dep,,sizeof(Dep));
         tou=;    wei=;
         q[]=S;    Dep[S]=;
         for(int u=S;u<=T;u++) E[u]=first[u];
         while(tou < wei)
         {
             int u=q[++tou];
             for(int e=first[u];e;e=next[e])
             {
                 int v=go[e];
                 if(Dep[v] || !w[e]) continue;
                 Dep[v] = Dep[u] + ;
                 q[++wei] = v;
             }
         }
         return Dep[T] > ;
 }

 int Dfs(int u,int Limit)
 {
         if(u==T || !Limit) return Limit;
         int flow=,f;
         for(int &e=E[u]; e; e=next[e])
         {
             int v=go[e];
             if(Dep[v]!=Dep[u]+ || !w[e]) continue;
             f=Dfs(v,min(w[e],Limit));
             w[e] -= f;
             w[((e-)^)+] += f;
             Limit -= f;
             flow += f;
             if (!Limit) break;
         }
         return flow;
 }

 int main()
 {
         n=get();    m=get();
         for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
         {
             a[i][j] = get();
         }

         int PD=n*m;
         S=;    T=*PD+;
         for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
         {
             if(a[i][j] == -)
             {
                 Max = a[i][j] = ;
                 Add(S,id(i,j),INF);
                 for(int k=i-;k>=;k--) Max = max(Max, a[k][j]);
                 for(int k=i;k>=+;k--) Add(id(k,j), id(k-,j), Max-a[k][j]);
                 Ans += Max;
             }

             else
             if(a[i][j] == -)
             {
                 Max = a[i][j] = ;
                 Add(S,id(i,j),INF);
                 for(int k=i+;k<=n;k++)    Max = max(Max, a[k][j]);
                 for(int k=i;k<=n-;k++) Add(id(k,j), id(k+,j), Max-a[k][j]);
                 Ans += Max;
             }

             else
             if(a[i][j] == -)
             {
                 Max = a[i][j] = ;
                 Add(id(i,j)+PD,T,INF);
                 for(int k=j-;k>=;k--) Max = max(Max, a[i][k]);
                 for(int k=j;k>=+;k--) Add(id(i,k-)+PD, id(i,k)+PD, Max-a[i][k]);
                 Ans += Max;
             }

             else
             if(a[i][j] == -)
             {
                 Max = a[i][j] = ;
                 Add(id(i,j)+PD,T,INF);
                 for(int k=j+;k<=m;k++) Max = max(Max, a[i][k]);
                 for(int k=j;k<=m-;k++) Add(id(i,k+)+PD, id(i,k)+PD, Max-a[i][k]);
                 Ans += Max;
             }

             else
             {
                 Add(id(i,j), id(i,j)+PD, INF);
             }
         }

         while(Bfs()) Ans-=Dfs(S,INF);

         printf("%d",Ans);
 }