Round 0: Regionals 2010 :: NEERC Eastern Subregional

Round 0: Regionals 2010 :: NEERC Eastern Subregional

贴吧题解（官方）？

网上的题解

水 A Murphy's Law

题意：Anka拿着一块涂着黄油的面包正要往嘴里塞，忽然虎躯一震面包脱手了。 面包可以被认为是一条长度为l的线段，脱手的一瞬间面包（线段）与地面平行，此时面包的下表面为黄油。面包脱手后在掉落过程中以一定的角速度绕面包中心（即线段中点）旋转。 问面包的哪一面先着地。

l:面包的长度，以厘米为单位；

h：Anka的嘴巴与地面的垂直距离，以厘米为单位；
w：面包的在掉落过程中每分钟的转数。

思路：(cyd)根据自由落体，当面包下落到l/2的高度时可以确定面包的旋转角度，根据这个角度可以确定面包最后落地的方式。

代码：

#include <bits/stdc++.h>
using namespace std;

const double g=9.81;
int L,H,W;
double l,h,w,pas;
int main()
{

    int i,j,k;
    while(scanf("%d %d %d",&L,&H,&W)!=EOF)
    {
        l=L,h=H,w=W;
        l=l/100.0,h=h/100.0;                 //单位转换
        w=w/60.0;
        pas=h-l/2;
        if(pas<=0)                           //特殊情况
        {
            printf("butter\n");
        }
        else
        {
            double t1=sqrt(pas*2.0/g),pr;
            pr=t1*w;
            pr=pr-(int)pr;                   //去掉整数圈数
            if(0.25<=pr && pr<0.75)
            {
                printf("bread\n");
            }
            else
            {
                printf("butter\n");
            }
        }
    }
    return 0;
}

　　

B The Revolution Cup

题意：将一大波球队分为t个等级，编号从1到t，编号越小表示该球队的能力越强。每个等级恰好有g支球队。这些球队由一些股东进行投资。要求将这总共g*t支球队分为g个小组，每个小组t至球队，使每个小组的球队同时满足两个条件：（1）等级各不相同；（2）股东各不相同。

思路：...

代码：...

C Cube Puzzle

题意：Anka生日的时候，Petka给送了一个自制的拼装积木：积木分为6块小积木，每块小积木有一个面积为n*n的底座，外表面涂漆，内表面分为n*n个正方小格子，其中可能有一些正方小格子附着长度为k的长方小柱子，柱子的长度不会超过n。 请帮帮Anka把这6块小积木组装成一个n*n*n的正方体。这6块小积木的体位可以随意旋转。

思路：...

代码：...

数论 D The Czechs' Rifles

题意：

火枪手dota被虐，跑到杰克那里买步枪。杰克有n只步枪，第1只步枪卖1元，第2只步枪卖1元，接下来第i只步枪的价格等于第(i-1)和第(i-2)只步枪的价格之和。
火枪手只有面值为1，k，k^2, k^3……（k的非负整数次幂）的钞票，火枪手买枪，会用钞票张数最少的方案按照步枪的价格购买每一只的步枪。
要求按照每一只步枪花费的钞票张数从小到大将步枪排序，若两只步枪所花费的钞票张数相同，则编号小的步枪排在前边。

思路：(cyd)题目即求Fibonacci的第n项K进制表示后各个位的和。由于题目所要求的数列值很大，采用压缩的方式，以最大的k ^ n（< 1000000）作为进制将数列转换，先预处理出来k ^ n各个数的位数之和以节省时间，然后直接采用滚动数组模拟加法的方法进行计算。

代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn=3005;
int n,k;
int mod;
int sum[1000005];

struct Node1
{
    int cnt_num;            //结果的位数和
    int id;                 //编号
}ans[50007];

struct Node
{
    int num[maxn];          //各位数的值
    int num_len;            //位数长度
    int getans()            //算出各位数之和
    {
        int ret=0;
        for(int i=0;i<num_len;i++)
        {
            ret+=sum[num[i]];
        }
        return ret;
    }
    Node()
    {
        num_len=0;
        memset(num,0,sizeof(num));
    }
};

struct Node a,b,c;

bool cmp(Node1 A,Node1 B)
{
    if(A.cnt_num==B.cnt_num)
        return A.id<B.id;
    else
        return A.cnt_num<B.cnt_num;
}

int main()
{
    int i,j,k;
    while(scanf("%d %d",&k,&n)!=EOF)
    {
        mod=k;
        while( mod*k <=1000000)         //算出最大的K^n
        {
            mod=mod*k;
        }
        for(int i=0;i<=mod;i++)         //预处理k^n里的各个数的位数之和
        {
            int x=i;
            int temp=0;
            while(x)
            {
                temp+=x%k;
                x/=k;
            }
            sum[i]=temp;
        }

        a.num[0]=1,a.num_len=1;b.num[0]=1,b.num_len=1;              //直接写出前两个数
        ans[1].cnt_num=1,ans[1].id=1;ans[2].cnt_num=1,ans[2].id=2;

        for(i=3;i<=n;i++)                                           //由前两位数得出值
        {
            int pre=0;
            for(j=0;j<a.num_len || j<b.num_len || pre;j++)
            {
                c.num[j]=(a.num[j]+b.num[j]+pre)%mod;               //当前位的值
                pre=(a.num[j]+b.num[j]+pre)/mod;                    //进位
            }
            c.num_len=j;
            ans[i].id=i;
            ans[i].cnt_num=c.getans();                              //计算位数和
            a=b;
            b=c;
        }

        sort(ans+1,ans+n+1,cmp);                                    //按照位数和大小，序号大小排序

        for(i=1;i<=n;i++)
        {
            if(i==n)
                printf("%d\n",ans[i].id);
            else
                printf("%d ",ans[i].id);
        }

    }
    return 0;
}

　　

暴力/数学思维 E The Machinegunners in a Playoff

题意：A和B在各自的足球场比赛，共比两场，给出其中一场A的得分数和B的得分数。问（1）A在第二场比赛至少进几球能有机会赢得比赛。（2）A在第二场比赛至多进几球使得B有机会赢得比赛。比赛规则是1. 如果两场总积分不同，则积分大的赢；2. 如果总积分相同，那么在客场比分大的赢；3. 如果还相同，那么随机决定输赢。

思路：考虑至少进球数时，假定B得分为0；考虑至多进球数时，假定B得分为30。解法一：（bh）考虑到每场比分最多30，可以直接枚举A的得分数，用规则判断是否合理。

解法二：(cyd)分类讨论法，以A队视角先分主场和客场情况，再根据赢、平、输（即输入的x,y大小比较）分类，共分为6类。问题一为A队有赢得比赛的可能，那么就让B队为最坏情况（进0球）来算A队至少进球数；问题二为B队有赢得比赛可能，那么让B队为最好情况（进30球）来算A队至多的进球数。

代码：

解法一：

#include <bits/stdc++.h>

bool home;

//A(a, c) B(b, d)
bool judge_min(int a, int b, int c, int d) {
    if (a + c == b + d) {
        if (home) {
            //a=homeA, b=awayB
            //c=awayA, d=homeB
            if (c >= b) {
                return true;
            } else {
                return false;
            }
        } else {
            //a=awayA, b=homeB
            //c=homeA, d=awayB
            if (a >= d) {
                return true;
            } else {
                return false;
            }
        }
    } else if (a + c > b + d) {
        return true;
    } else {
        return false;
    }
}

bool judge_max(int a, int b, int c, int d) {
    if (a + c == b + d) {
        if (home) {
            //a=homeA, b=awayB
            //c=awayA, d=homeB
            if (c <= b) {
                return true;
            } else {
                return false;
            }
        } else {
            //a=awayA, b=homeB
            //c=homeA, d=awayB
            if (a <= d) {
                return true;
            } else {
                return false;
            }
        }
    } else if (a + c < b + d) {
        return true;
    } else {
        return false;
    }
}

int main() {
    int T;
    scanf ("%d", &T);
    getchar ();
    char str[100];
    while (T--) {
        int x, y;
        gets (str);
        sscanf (str, "The Machinegunners played %s game, scored %d goals, and conceded %d goals.", &str, &x, &y);

        if (str[0] == 'h') {
            home = true;
        } else {
            home = false;
        }

        int minA, maxA;
        for (int i=0; i<=30; ++i) {
            if (judge_min (x, y, i, 0)) {
                minA = i;
                break;
            }
        }
        for (int i=30; i>=0; --i) {
            if (judge_max (x, y, i, 30)) {
                maxA = i;
                break;
            }
        }
        printf ("%d %d\n", minA, maxA);
    }
    return 0;
}

解法二：

#include <bits/stdc++.h>
using namespace std;

int main() {
    int T;
    scanf ("%d", &T);
    getchar ();
    char str[100];
    while (T--) {
        int x, y;
        gets (str);
        sscanf (str, "The Machinegunners played %s game, scored %d goals, and conceded %d goals.", &str, &x, &y);
        //printf ("$%s\n", str);
        //printf ("$%d %d\n", x, y); continue;
        int minA,maxA;                              //最少进球数和最大进球数
        if (str[0] == 'h') {                        //主场比赛情况
            if(x>y)                                 //赢
            {
                minA=0;
                if(x==30)
                    maxA=y+30-x;
                else
                    maxA=y+30-x-1;
            }
            else if(x==y)                           //平
            {
                if(x==0)
                    minA=0;
                else
                    minA=1;
                if(x==30)
                    maxA=30;
                else
                    maxA=29;
            }
            else                                    //输
            {
                if(x==0)
                    minA=y;
                else
                    minA=y-x+1;
                maxA=30;
            }
        } else if (str[0] == 'a') {                 //客场比赛情况
            if(x>y)
            {
                minA=0;
                maxA=y+30-x;
            }
            else if(x==y)
            {
                minA=0;
                maxA=30;
            }
            else
            {
                minA=y-x;
                maxA=30;
            }
        }
        minA = max (minA, 0);
        minA = min (minA, 30);
        maxA = max (maxA, 0);
        maxA = min (maxA, 30);
        printf ("%d %d\n", minA, maxA);
    }
    return 0;
}

　　

构造 F Chapaev and a Cipher Grille

题意：一个n*n的正方形，选择n*n/4个位置”开天窗”，正方形旋转四次，那么这m个格子都能经旋转获得四个位置，要使每个格子的四个位置都不重复才能覆盖整个图。求字典序第k个的方案。

样例：

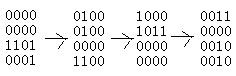
所谓的字典序就是排列成n*n的线性序列后比较大小，如（0000000011010001）比（010001000000100）要小。

思路：（bh）网上有详细分析，链接。里面的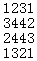这个意思是说相同的数字(1~4)只要某一个填1就可以了（因为可以旋转得到）。简单来说，做法就是假设该位置不填1（字典小），那么后面填数字的总方案数和k比较，如果小于k，说明前面所有方案数都不行，k-前面所有的方案数，同时该位置填1；如果大于k，说明k在前面的总方案数里面。

代码：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 100 + 5;
int a[N][N], q[N], ans[N];
int vis[N];
int n;
ll k;

void prepare(int n) {
    //m：左上角m*m小正方形，num：要填的数字
    int m = n / 2, num = 0;
    for (int i=1; i<=m; ++i) {
        for (int j=1; j<=m; ++j) {
            a[i][j] = a[j][n-i+1] = a[n-i+1][n-j+1] = a[n-j+1][i] = ++num;
        }
    }
    //转变为n*n的线性序列
    m = 0;
    for (int i=1; i<=n; ++i) {
        for (int j=1; j<=n; ++j) {
            q[++m] = a[i][j];
        }
    }
}

int main() {
    while (scanf ("%d%I64d", &n, &k) == 2) {
        prepare (n);
        memset (ans, 0, sizeof (ans));

        //m：一共要填的数字个数；每个数字在整张图中出现4次
        int m = n * n / 4, len = n * n;
        ll tot = 1;
        for (int i=1; i<=m; ++i) {
            vis[i] = 4;  //初始化能填的位置都有4个
            tot *= 4;  //4 ^ m
        }

        for (int i=1; i<=len; ++i) {
            if (vis[q[i]] > 0) {
                int v = vis[q[i]];
                ll pretot = tot / v;
                if (v > 1) {
                    //如果不选, 这个数字能填的位置还有(v-1)个
                    pretot *= (v - 1);
                }

                //因为要字典序第k个，如果在这里填数字的话，字典序是比不填大的

                //所以先算前面的填了这个数字后所有方案数，pretot如果
                if (k > pretot) {
                    //如果k>pretot，那么这个数字一定要填在这里
                    k -= pretot;
                    tot -= pretot;
                    ans[i] = 1;
                    vis[q[i]] = -1;  //接下来这个数字都不填了
                } else {
                    tot = pretot;  //新的总个数
                    vis[q[i]]--;
                    if (!vis[q[i]]) {
                        //后面没了，只能填在这里
                        ans[i] = 1;
                    }
                }
                if (!k) {
                    break;
                }
            }
        }

        for (int i=1; i<=n; ++i) {
            for (int j=1; j<=n; ++j) {
                printf ("%d", ans[(i-1)*n+j]);
            }
            puts ("");
        }
    }
    return 0;
}

最短路 G Mobile Telegraphs

题意：n个电话机，每一个用不同的10位0~9的数字表示，电话机A和电话机B可以通话的条件是1. 改变A的某一个数字能变成B 2. 或者A的两个数字交换能变成B。A和B的连线消耗时间为它们的最长公共前缀长度，问从电话机1到电话机n所消耗的最少连线时间。

思路：（bh）A和B能通话，就相当于A到B有一条边，边权值为消耗时间。问题转换为求1到n的最短路。本题一个关键点是图的边的数量并不是n*n，而是10*9+10*9/2=135种。这样的话可以用map来找改变后是否存在这样的电话机。

代码：

#include <bits/stdc++.h>

typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 5e4 + 5;
const int E = N * 150 * 2;
int cost[15];
ll ten_pow[15];
ll s[N];
int d[N];
int prev[N];
bool vis[N];

struct Edge {
    int v, w, nex;
}edge[E];
int head[N];
int n, etot;

void SPFA(int s) {
    memset (d, INF, sizeof (d));
    memset (vis, false, sizeof (vis));
    d[s] = 0; vis[s] = true;
    std::queue<int> que;
    que.push (s);
    while (!que.empty ()) {
        int u = que.front ();
        que.pop ();
        vis[u] = false;
        for (int i=head[u]; ~i; i=edge[i].nex) {
            Edge e = edge[i];
            if (d[e.v] > d[u] + e.w) {
                d[e.v] = d[u] + e.w;
                prev[e.v] = u;
                if (!vis[e.v]) {
                    vis[e.v] = true;
                    que.push (e.v);
                }
            }
        }
    }
}

void add_edge(int u, int v, int w) {
    edge[etot].v = v; edge[etot].w = w;
    edge[etot].nex = head[u]; head[u] = etot++;
}

void init_edge() {
    memset (head, -1, sizeof (head));
    etot = 0;
}

void print(int u, std::vector<int> &path) {
    if (u == 1) {
        return ;
    }
    print (prev[u], path);
    path.push_back (prev[u]);
}

void init_ten_pow() {
    ten_pow[0] = 1;
    for (int i=1; i<15; ++i) {
        ten_pow[i] = ten_pow[i-1] * 10;
    }
}

int main() {
    init_ten_pow ();
    while (scanf ("%d", &n) == 1) {
        std::map<ll, int> ID;
        std::map<ll, int>::iterator it;

        for (int i=0; i<10; ++i) {
            scanf ("%d", &cost[i]);
        }
        for (int i=1; i<=n; ++i) {
            scanf ("%I64d", &s[i]);
            ID[s[i]] = i;
        }

        init_edge ();
        for (int i=1; i<=n; ++i) {
            for (int j=1; j<=10; ++j) {
                for (int k=0; k<=9; ++k) {
                    ll tmp = s[i];
                    int d = (tmp / ten_pow[j-1]) % 10;
                    //d -> k
                    if (d == k) {
                        continue;
                    }
                    tmp = tmp - (d - k) * ten_pow[j-1];
                    it = ID.find (tmp);
                    if (it != ID.end ()) {
                        add_edge (i, it->second, cost[10-j]);
                    }
                }
            }
            for (int j=1; j<=10; ++j) {
                for (int k=j-1; k>=1; --k) {
                    ll tmp = s[i];
                    int d1 = (tmp / ten_pow[j-1]) % 10;
                    int d2 = (tmp / ten_pow[k-1]) % 10;
                    //d1 <-> d2
                    if (d1 == d2) {
                        continue;
                    }
                    tmp = tmp - (d1 - d2) * ten_pow[j-1];  //j <- k
                    tmp = tmp - (d2 - d1) * ten_pow[k-1];  //k <- j
                    it = ID.find (tmp);
                    if (it != ID.end ()) {
                        add_edge (i, it->second, cost[10-j]);
                    }
                }
            }
        }

        SPFA (1);
        if (d[n] == INF) {
            puts ("-1");
        } else {
            printf ("%d\n", d[n]);
            std::vector<int> path;
            print (n, path);
            path.push_back (n);
            printf ("%d\n", path.size ());
            for (int i=0; i<path.size (); ++i) {
                if (i > 0) {
                    putchar (' ');
                }
                printf ("%d", path[i]);
            }
            puts ("");
        }
    }
    return 0;
}

H

题意：给出一个正整数n（n为合数），求n的一个划分(a1,a2,...,ak,...)(k>=2)。使得其在存在最大的最大公约数之下，存在最大的最小公倍数。

思路：(cyd)首先，要想有最大公公约数，那么假设它们的最大公约数为G，那么:G*(a1/G,a2/G,a3，...)=n,所以要想让G最大，那么只需要a1/G+a2/G+a3/G+...最小记为M，那么取M为n的最小素数因子即可。这样一来：M<=sqrt(10^9)<31625。LCM的一个定理:LCM(a1,a2,a3,...,ai)为各个数分解质因数以后，所有存在的素数的最高幂次之积。问题转换为求素数M的一个划分，使划分中的数的嘴小公倍数最大。

根据定理，我们可以断言：将拆分成M=若干个1+p1^k1+p2^k2+p3^k3+...（其中p1,p2,p3,...等数两两互质且为素数）时，最小公倍数最大。
最后变为对各个素数的指数的动态规划问题。因为每两个数都是互质的，所以其最小公倍数即为已经存在的各个数之积，因为不需要求解LCM，所以大可用double存储。如果害怕double过大时，存在前十六位相同，导致状态转移错无，那我们可以用log来表示，因为：log是单增函数，且log(a*b)=loga+logb，便于状态转移。

double dp[N][M];(M:minprime)
int pre[i][j];
我们用dp[i][j]表示用前i个数表示j时最优解，即log的最大值。
用pre[i][j]表示取dp[i][j]为最优解表示j时，j剩余的数。
状态转移方程:dp[i][j]=max(dp[i-1][j-p[i]]+(Kn)*logp[i],dp[i][j]);
这样我们最后的最优解即为:dp[N][M]：如果:M-pre[N][M]不为零的话就要输出(M-pre[N][M])*G,接下来搜索dp[N-1][j-k*prime[N]](即dp[N-1][M]，M=pre[N][M])。
最后dp[1][M]剩下来的值即为要输出的1*G的个数了。

其中对n%2，n%3的预处理可以省去很多麻烦，而且少了一大半的数

代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn = 100007;
int vis[maxn], prime[maxn], prime_num;
int n,minprime,magcd,malcm,pre[156][35000];
double dp[160][35000];

void getprime()                                 //处理前十万范围内的素数
{
    memset(vis, 0, sizeof(vis));
    for (int i = 2; i <= sqrt(maxn * 1.0); i++) {
        if (!vis[i]) {
            for (int j = i * i; j < maxn; j += i) {
                vis[j] = 1;
            }
        }
    }
    prime_num = 0;
    for (int i = 2; i < maxn; i++) {
        if (!vis[i]) {
            prime[++prime_num] = i;
        }
    }
}

int main()
{
    int i,j,k;
    int flg=1;

    scanf("%d",&n);

    getprime();
    for(i=1;i<=prime_num;i++)           //算出最小的素数因子
    {
        if(n%prime[i]==0)
        {
            flg=1;
            minprime=prime[i];
            break;
        }
    }
    if(flg==0)
    {
        minprime=n;
    }

    magcd=n/minprime;                   //最大公约数
    malcm=0;

    if(minprime==2)                     //对n%2，n%3的预处理
    {
        printf("%d %d\n",magcd,magcd);
        return 0;
    }
    if(minprime==3)
    {
        printf("%d %d\n",magcd,magcd*2);
        return 0;
    }
    for(i=1;i<=150;i++)                 //只需处理前一小部分素数
    {
        for(j=0;j<=minprime;j++)
        {
            dp[i][j]=dp[i-1][j];
            pre[i][j]=j;
            int cnt=prime[i];           //当前素数对值的贡献
            double t=log((double)prime[i]),temp;
            for(k=1;cnt<=j;k++)
            {
                temp=t*(double)k;                   //k*log(p)的值
                if(dp[i][j]<dp[i-1][j-cnt]+temp)
                {
                    dp[i][j]=dp[i-1][j-cnt]+temp;
                    pre[i][j]=j-cnt;
                }
                cnt*=prime[i];                      //p的k次方
            }
        }
    }

    int tot=minprime;
    for(i=150;i>=1;i--)
    {
        if(tot-pre[i][tot]!=0)                      //该素数对值有贡献
        {
            printf("%d ",(tot-pre[i][tot])*magcd);
            tot=pre[i][tot];
        }
    }
    while(tot)                                      //算出1的个数
    {
        printf("%d ",magcd);
        tot--;
    }
    printf("\n");
    return 0;
}

　　

I

题意：...

思路：...

代码：...

暴力 J Chapaev and Potatoes

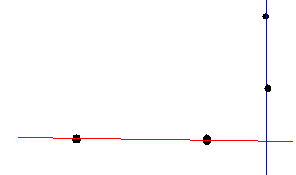
题意：四个点在20*20的格子里，问最少要移动几个点，使得存在两个点在同一条竖线或横线，且另外两个也在另一条竖线或横线，如图所示：

思路：（bh）最多重排2个土豆的位置。枚举0个/1个/2个点不动，暴力重排剩余的点，判断是否符合条件，复杂度O(N^4)。

代码：

#include <bits/stdc++.h>

int x[4], y[4];

void print() {
    for (int i=0; i<4; ++i) {
        printf ("%d %d\n", x[i], y[i]);
    }
}

bool judge() {
    int c[4] = {0};
    int X[4] = {x[0], x[1], x[2], x[3]};
    int Y[4] = {y[0], y[1], y[2], y[3]};
    for (int i=0; i<4; ++i) {
        for (int j=i+1; j<4; ++j) {
            if (X[i] == X[j] && Y[i] == Y[j]) {
                return false;
            }
            if (X[i] == X[j] || Y[i] == Y[j]) {
                c[i]++; c[j]++;
            }
        }
    }
    for (int i=0; i<4; ++i) {
        if (c[i] != 1) {
            return false;
        }
    }
    return true;
}

void solve() {
    //move 0
    if (judge ()) {
        print ();
        return ;
    }
    //move 1
    for (int i=0; i<4; ++i) {
        int tx = x[i], ty = y[i];
        for (int p=1; p<=20; ++p) {
            for (int q=1; q<=20; ++q) {
                x[i] = p; y[i] = q;
                if (judge ()) {
                    print ();
                    return ;
                }
            }
        }
        x[i] = tx; y[i] = ty;
    }
    //move 2
    for (int i=0; i<4; ++i) {
        for (int j=0; j<4; ++j) {
            int tx1 = x[i], ty1 = y[i];
            int tx2 = x[j], ty2 = y[j];
            for (int p1=1; p1<=20; ++p1) {
                for (int q1=1; q1<=20; ++q1) {
                    for (int p2=1; p2<=20; ++p2) {
                        for (int q2=1; q2<=20; ++q2) {
                            x[i] = p1; y[i] = q1;
                            x[j] = p2; y[j] = q2;
                            if (judge ()) {
                                print ();
                                return ;
                            }
                        }
                    }
                }
            }
            x[i] = tx1; y[i] = ty1;
            x[j] = tx2; y[j] = ty2;
        }
    }
}

int main() {
    while (scanf ("%d%d", &x[0], &y[0]) == 2) {
        for (int i=1; i<4; ++i) {
            scanf ("%d%d", &x[i], &y[i]);
        }
        solve ();
    }
    return 0;
}