[CSP-S模拟测试]:小P的2048（模拟）

题目描述

　　最近，小$P$迷上了一款叫做$2048$的游戏。这块游戏在一个$n\times n$的棋盘中进行，棋盘的每个格子中可能有一个形如$2^k(k\in N^*)$的数，也可能是空的。游戏规则介绍如下：
　　$1.$游戏开始时棋盘内将会生成两个数字，生成的数字仅可能为$2$或$4$；
　　$2.$每次操作，玩家可以选择上、下、左、右四个方向进行平移；
　　$3.$以向上平移为例，从上往下考虑每个不为空的格子，若上方与之相邻的格子为空，则将该格子上的数字移动至相邻格子。在一次位移中，每个数字会进行多次移动直到不能移动为止。
　　$4.$以向上平移为例，从上往下考虑每个不为空的格子，若上方与之相邻的数字恰好与其相等，则两个数字可以合并，新生成的数字为原来两个数之和。在一次合并中，每个数字只能与其它数合并一次，可以同时合并多对数字，但不能连续合并；
　　$5.$每次操作由位移+合并+位移组成，若操作后棋盘局面发生变化，则该操作为有效操作，其有效得分为合并过程中所有新生成的数字之和；
　　$6.$在每次操作后，棋盘内都会新生成一个数字$2$或$4$，数字只会在空格子处生成；
　　$7.$当棋盘被数字填满，玩家无法进行任何有效操作时，游戏结束，游戏总得分为所有操作的有效得分之和。

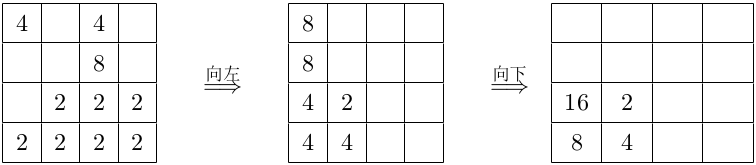
　　为了降低难度，小$P$对$2048$游戏进行了一些改动。在游戏开始前，小$P$会告诉你棋盘的初始状态，并给你若干次操作。每次操作由方向变量、位置参数和一个数字组成，方向变量代表你在本次操作中的移动方向，给定的数字为本次操作之后将会生成的数字的大小，而位置参数将决定生成数字的位置。若位置参数为$K$，操作后棋盘中空格子的数量为$r$，则生成数字的位置从上到下、从左到右第$(1+K\mod r)$个空格子。如果每次操作为无效操作，则游戏结束，而当所有操作都完成后，游戏同样结束。（注意：改动后，游戏结束时棋盘不一定被数字填满。）

　　现在小$P$问你，在游戏结束前你一共进行了多少次有效操作，最后你的游戏总得分是多少。

---

输入格式

　　第一行为两个正整数$n$和$m$，分别表示棋盘的大小和操作的个数。
　　第二行为六个正整数$x_1,y_1,v_1$和$x_2,y_2,v_2$（$x_1,y_1,x_2,y_2\leqslant n,v_1,v_2\in\{2,4\}$），分别代表游戏开始时，棋盘上两个数字的位置（行/列）的大小。行号从上往下的编号，列号从左往右的编号，编号均以$1$开始。
　　接下来$m$行，表示小$P$给你的$m$个操作。每行由三个自然数$D_i,K_i,V_i$组成，其中$D_i$代表本次操作的平移方向，$0/1/2/3$分别代表上/下/左/右。$K_i$为位置参数，$V_i$为操作后生成的数的大小。（$D_i\in\{0,1,2,3\},K_i<2^{31},V_i\in\{2,4\}$）

---

输出格式

　　输出共两行，每行一个正证书，分别代表你完成的有效操作数与游戏总得分。

---

样例

样例输入：

3 6
2 1 2 3 2 4
1 14 2
1 6 4
2 10 2
0 3 2
2 17 2
3 14 4

样例输出：

4
12

---

数据范围与提示

样例解释：

四次有效操作后，棋盘无法继续向左平移，故游戏结束，总得分为$4+8=12$。

数据范围：

对于$10\%$的数据：$n=2$
对于$40\%$的数据：$n\leqslant 4,m\leqslant 100$
对于$100\%$的数据：$2\leqslant n\leqslant 8,1\leqslant m\leqslant 100000$

---

题解

大模拟，注意以下几点：

　　$\alpha.$输出格式。

　　$\beta.$大样例中没有向右的操作，所以要特别注意向右（考试时因为这个挂到飞起……）

　　$\gamma.$数组勤清空。

　　$\delta.$有数据点一开始的两个坐标是一个，所以避免使用记录空格子的个数的方法。

时间复杂度：$\Theta(n^2m)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y,v,x2,y2,v2;
int Map[10][10];
long long ans;
int que[10];
bool up(int k,int v)
{
	bool res=0;
	int r=0;
	for(int i=1;i<=n;i++)
	{
		memset(que,0,sizeof(que));
		for(int j=1;j<=n;j++)
			if(Map[j][i])
			{
				if(j>1&&!Map[j-1][i])res=1;
				que[++que[0]]=Map[j][i];
			}
		for(int j=1;j<=n;j++)
			Map[j][i]=que[j];
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(Map[j][i]==Map[j+1][i]&&Map[j][i])
			{
				res=1;
				Map[j][i]<<=1;
				Map[j+1][i]=0;
				ans+=Map[j][i];
			}
	for(int i=1;i<=n;i++)
	{
		memset(que,0,sizeof(que));
		for(int j=1;j<=n;j++)
			if(Map[j][i])
			{
				if(j>1&&!Map[j-1][i])res=1;
				que[++que[0]]=Map[j][i];
			}
		for(int j=1;j<=n;j++)
			Map[j][i]=que[j];
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!Map[i][j])r++;
	if(!r)return 0;
	r=1+k%r;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!Map[i][j])
			{
				r--;
				if(!r){Map[i][j]=v;goto nxt;}
			}
	nxt:return res;
}
bool down(int k,int v)
{
	bool res=0;
	int r=0;
	for(int i=1;i<=n;i++)
	{
		memset(que,0,sizeof(que));
		for(int j=n;j;j--)
			if(Map[j][i])
			{
				if(j<n&&!Map[j+1][i])res=1;
				que[++que[0]]=Map[j][i];
			}
		int now=que[0];
		reverse(que+1,que+que[0]+1);
		for(int j=n;j;j--)
		{
			if(now)Map[j][i]=que[now--];
			else Map[j][i]=0;
		}
	}
	for(int i=1;i<=n;i++)
		for(int j=n;j;j--)
			if(Map[j][i]==Map[j-1][i]&&Map[j][i])
			{
				res=1;
				Map[j][i]<<=1;
				Map[j-1][i]=0;
				ans+=Map[j][i];
			}
	for(int i=1;i<=n;i++)
	{
		memset(que,0,sizeof(que));
		for(int j=n;j;j--)
			if(Map[j][i])
			{
				if(j<n&&!Map[j+1][i])res=1;
				que[++que[0]]=Map[j][i];
			}
		int now=que[0];
		reverse(que+1,que+que[0]+1);
		for(int j=n;j;j--)
		{
			if(now)Map[j][i]=que[now--];
			else Map[j][i]=0;
		}
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!Map[i][j])r++;
	if(!r)return 0;
	r=1+k%r;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!Map[i][j])
			{
				r--;
				if(!r){Map[i][j]=v;goto nxt;}
			}
	nxt:return res;
}
bool left(int k,int v)
{
	bool res=0;
	int r=0;
	for(int i=1;i<=n;i++)
	{
		memset(que,0,sizeof(que));
		for(int j=1;j<=n;j++)
			if(Map[i][j])
			{
				if(j>1&&!Map[i][j-1])res=1;
				que[++que[0]]=Map[i][j];
			}
		for(int j=1;j<=n;j++)
			Map[i][j]=que[j];
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(Map[i][j]==Map[i][j+1]&&Map[i][j])
			{
				res=1;
				Map[i][j]<<=1;
				Map[i][j+1]=0;
				ans+=Map[i][j];
			}
	for(int i=1;i<=n;i++)
	{
		memset(que,0,sizeof(que));
		for(int j=1;j<=n;j++)
			if(Map[i][j])
			{
				if(j>1&&!Map[i][j-1])res=1;
				que[++que[0]]=Map[i][j];
			}
		for(int j=1;j<=n;j++)
			Map[i][j]=que[j];
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!Map[i][j])r++;
	if(!r)return 0;
	r=1+k%r;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!Map[i][j])
			{
				r--;
				if(!r){Map[i][j]=v;goto nxt;}
			}
	nxt:return res;
}
bool right(int k,int v)
{
	bool res=0;
	int r=0;
	for(int i=1;i<=n;i++)
	{
		memset(que,0,sizeof(que));
		for(int j=n;j;j--)
			if(Map[i][j])
			{
				if(j<n&&!Map[i][j+1])res=1;
				que[++que[0]]=Map[i][j];
			}
		int now=que[0];
		reverse(que+1,que+que[0]+1);
		for(int j=n;j;j--)
		{
			if(now)Map[i][j]=que[now--];
			else Map[i][j]=0;
		}
	}
	for(int i=1;i<=n;i++)
		for(int j=n;j;j--)
			if(Map[i][j]==Map[i][j-1]&&Map[i][j])
			{
				res=1;
				Map[i][j]<<=1;
				Map[i][j-1]=0;
				ans+=Map[i][j];
			}
	for(int i=1;i<=n;i++)
	{
		memset(que,0,sizeof(que));
		for(int j=n;j;j--)
			if(Map[i][j])
			{
				if(j<n&&!Map[i][j+1])res=1;
				que[++que[0]]=Map[i][j];
			}
		int now=que[0];
		reverse(que+1,que+que[0]+1);
		for(int j=n;j;j--)
		{
			if(now)Map[i][j]=que[now--];
			else Map[i][j]=0;
		}
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!Map[i][j])r++;
	if(!r)return 0;
	r=1+k%r;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!Map[i][j])
			{
				r--;
				if(!r){Map[i][j]=v;goto nxt;}
			}
	nxt:return res;
}
int main()
{
	scanf("%d%d%d%d%d%d%d%d",&n,&m,&x,&y,&v,&x2,&y2,&v2);
	Map[x][y]=v;Map[x2][y2]=v2;
	for(int i=1;i<=m;i++)
	{
		int d,k,v;
		scanf("%d%d%d",&d,&k,&v);
		if(d==0)if(!up(k,v)){printf("%d\n%lld\n",i-1,ans);return 0;}
		if(d==1)if(!down(k,v)){printf("%d\n%lld\n",i-1,ans);return 0;}
		if(d==2)if(!left(k,v)){printf("%d\n%lld\n",i-1,ans);return 0;}
		if(d==3)if(!right(k,v)){printf("%d\n%lld\n",i-1,ans);return 0;}
	}
	printf("%d\n%lld\n",m,ans);
	return 0;
}

---

rp++