前缀和序列 & 差分序列

前缀和序列

所谓前缀和数组，就是从第一个元素到当前元素的和。假设这个前缀和数组为d[]，原数组为a[]，那么d[ i ] = a[ 1 ]+a[ 2 ]+a[ 3 ]+...+a[ i-1 ]+a[ i ]。在实际应用中，可以直接d[ i ]=d[ i-1 ]+a[ i ]。

它主要用于查询一段区间的和（i,j）= d[ j ]  -  d[ i-1 ] 。

初始化的时间复杂度为O(n)，每一次查询的时间复杂度为O(1)。

差分序列

所谓差分数组，就是这一个元素与上一个元素的差。假设这个差分数组为d[ ]，原数组为a[ ]，那么d[ i ] = a[ i ] - a[ i-1 ]。

它主要用于区间增加和单点查询。、

区间增加：根据定义，很显然，在给（i，j）区间加x时，只需将d[ i ] += x ; d[ j+1 ] -=x 即可。

单点查询：有两种方法：

1. 求差分序列的前缀和--改变了d数组

   for(int i=1;i<=n;i++)  d[i]+=d[i-1];

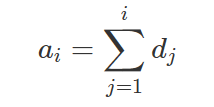2. --改变了a数组

   for(int i=;i<=n;i++) a[i]=a[i-]+d[i];

   可以根据自己的需求来选择方法

感性理解一下

初始化的时间复杂度为O(n),区间增加的时间复杂度为O(1)，单点查询的时间复杂度为O(n)。

总结

这两个序列不会单独考，但是经常会用在一些算法或者数据结构中，往往可以大大提高算法的效率。