POJ 2653 Pick-up sticks（几何）

Pick-up sticks

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 13377		Accepted: 5039

Description

Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.

Input

Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.

Output

For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.

The picture to the right below illustrates the first case from input.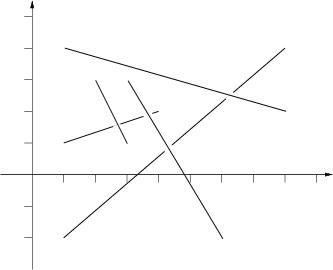

Sample Input

5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0

Sample Output

Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.

Hint

Huge input,scanf is recommended.

Source

Waterloo local 2005.09.17

 

 

题解：

　　几何模板题目

　　

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <string>
 #include <algorithm>
 #include <cmath>
 #include <vector>
 #include <queue>
 #include <map>
 #include <stack>
 #include <set>
 using namespace std;
 typedef long long LL;
 #define ms(a, b) memset(a, b, sizeof(a))
 #define pb push_back
 #define mp make_pair
 #define eps 0.0001
 const LL INF = 0x7fffffff;
 const int inf = 0x3f3f3f3f;
 const int mod = 1e9+;
 const int maxn = +;
 int n, cnt;
 struct POINT
 {
     double x, y, z;
     POINT():x(), y(), z(){};
     POINT(double _x_, double _y_, double _z_ = ):x(_x_), y(_y_), z(_z_) {};
 };
 struct SEG
 {
     POINT a;
     POINT b;
     SEG(){};
     SEG(POINT _a_, POINT _b_):a(_a_),b(_b_) {};
 };
 double Cross(const POINT &a, const POINT & b, const POINT &o)//叉乘
 {
     return (a.x - o.x)*(b.y - o.y) - (b.x - o.x)*(a.y - o.y);
 }
 bool IsIntersect(const SEG &u, const SEG &v)
 {
     return (Cross(v.a, u.b, u.a)*Cross(u.b, v.b, u.a)>=)&&
         (Cross(u.a, v.b, v.a)*Cross(v.b, u.b, v.a)>=)&&
         (max(u.a.x, u.b.x) >= min(v.a.x, v.b.x))&&
         (max(v.a.x, v.b.x) >= min(u.a.x, u.b.x))&&
         (max(u.a.y, u.b.y) >= min(v.a.y, v.b.y))&&
         (max(v.a.y, v.b.y) >= min(u.a.y, u.b.y));
 }
 int ans[maxn];
 SEG stick[maxn];
 void init()
 {
     cnt = ;
 }
 void solve() {
     double a, b, c, d;
     for(int i = ;i<=n;i++){
         scanf("%lf%lf%lf%lf", &a, &b, &c, &d);
         stick[i].a.x=a;stick[i].a.y=b;
         stick[i].b.x=c;stick[i].b.y=d;
     }
     for(int i = n;i>;i--){
         bool flag = ;
         for(int j = i+;j<=n;j++){
             if(IsIntersect(stick[i], stick[j])){
                 flag = ;
                 break;
             }
         }
         if(flag){
             ans[cnt++] = i;
         }
         if(cnt>=){
             break;
         }
     }
     printf("Top sticks:");
     for(int i = cnt-;i>=;i--){
         if(i==)    printf(" %d.",ans[i]);
         else printf(" %d,",ans[i]);
     }
     printf("\n");
 }
 int main() {
 #ifdef LOCAL
     freopen("input.txt", "r", stdin);
 //        freopen("output.txt", "w", stdout);
 #endif
     while(~scanf("%d", &n)&&n){
         init();
         solve();
     }
     return ;
 }