codeforces 447E or 446C 线段树 + fib性质或二次剩余性质

CF446C题意：

给你一个数列\(a_i\)，有两种操作：区间求和；\(\sum_{i=l}^{r}(a[i]+=fib[i-l+1])\)。\(fib\)是斐波那契数列。

思路

（一）

codeforces 447E or 446C

\(fib[n] = \frac{\sqrt5}{5}\times [(\frac{1+\sqrt5}{2})^n-(\frac{1-\sqrt5}{2})^n]\)

有关取模、同余、逆元的一些东西：

\(p = 1e9 + 9\)

\(383008016^2 ≡ 5 (mod\;p)\)

\(383008016 ≡ \sqrt5 (mod\;p)\)

\(\frac{1}{\sqrt5}≡276601605(mod\;p)\)

\(383008016的逆元 = 276601605\)

\((1+\sqrt5)/2≡691504013(mod\;p)\)

\(383008017\times 2的逆元 = 691504013\)

\((1-\sqrt5)/2≡308495997(mod\;p)\)

\((p-383008016+1)\times 2的逆元 = 308495997\)

\(fib[n] = 276601605\times [(691504013)^n-(308495997)^n] (mod\;\;p)\)

等比数列求和：\(sum = \frac{a}{a-1} \times (a^n - 1) (mod\;\;p) = a^2(a^n-1)(mod\;\;p)=a^{n+2}-a^2(mod\;\;p)\)

当\(p=1e9+9, a = 691504013或308495997时成立\)。

所以本题我们只需要用线段树lazy标记维护两个等比数列第一项为一次项的系数即可。代码如下。

#include<bits/stdc++.h>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;

const int MXN = 5e5 + 6;
const int INF = 0x3f3f3f3f;
const LL mod = 1000000009;
const LL p1 = 691504013;
const LL p2 = 308495997;
const LL p3 = 276601605;

int n, m;
LL ar[MXN], pre[MXN], mul1[MXN], mul2[MXN];
LL sum[MXN<<2], lazy1[MXN<<2], lazy2[MXN<<2];
LL ksm(LL a, LL b) {
    LL res = 1;
    for(;b;b>>=1,a=a*a%mod) {
        if(b&1) res = res * a %mod;
    }
    return res;
}
void check(LL &a) {
    if(a >= mod) a %= mod;
}
void push_up(int rt) {
    sum[rt] = sum[lson] + sum[rson]; check(sum[rt]);
}
void push_down(int l,int r,int rt) {
    if(lazy1[rt] == 0 && lazy2[rt] == 0) return;
    LL a = lazy1[rt], b = lazy2[rt];
    int mid = (l + r) >> 1;
    int len1 = mid-l+1, len2 = r - mid;
    lazy1[lson] += a; lazy2[lson] += b;
    sum[lson] = sum[lson] + a*((mul1[len1+2]-mul1[2])%mod+mod); check(sum[lson]);
    sum[lson] = (sum[lson] - b*((mul2[len1+2]-mul2[2])%mod+mod))%mod + mod; check(sum[lson]);
    lazy1[rson] += a*mul1[len1]%mod; lazy2[rson] += b*mul2[len1]%mod;
    sum[rson] = sum[rson] + a*mul1[len1]%mod*((mul1[len2+2]-mul1[2])%mod+mod); check(sum[rson]);
    sum[rson] = (sum[rson] - b*mul2[len1]%mod*((mul2[len2+2]-mul2[2])%mod+mod))%mod + mod; check(sum[rson]);
    lazy1[rt] = lazy2[rt] = 0;
    check(lazy1[lson]);check(lazy1[rson]);check(lazy2[lson]);check(lazy2[rson]);
}
void update(int L,int R,int l,int r,int rt,LL x,LL y) {
    if(L <= l && r <= R) {
        lazy1[rt] += x; lazy2[rt] += y;
        check(lazy1[rt]); check(lazy2[rt]);
        sum[rt] = sum[rt] + x*((mul1[r-l+3]-mul1[2])%mod+mod); check(sum[rt]);
        sum[rt] = (sum[rt] - y*((mul2[r-l+3]-mul2[2])%mod+mod))%mod + mod; check(sum[rt]);
        return;
    }
    push_down(l, r, rt);
    int mid = (l + r) >> 1;
    if(L > mid) update(L,R,mid+1,r,rson,x,y);
    else if(R <= mid) update(L,R,l,mid,lson,x,y);
    else {
        update(L,mid,l,mid,lson,x,y);
        update(mid+1,R,mid+1,r,rson,mul1[mid-L+1]*x%mod,mul2[mid-L+1]*y%mod);
    }
    push_up(rt);
}
LL query(int L,int R,int l,int r,int rt) {
    if(L <= l && r <= R) {
        return sum[rt];
    }
    push_down(l,r,rt);
    int mid = (l+r) >> 1;
    if(L > mid) return query(L,R,mid+1,r,rson);
    else if(R <= mid) return query(L,R,l,mid,lson);
    else {
        LL ans = query(L,mid,l,mid,lson);
        ans += query(mid+1,R,mid+1,r,rson);
        check(ans);
        return ans;
    }
}
int main() {
    //printf("%d\n", ksm(691504013-1,mod-2));
    //printf("%d\n", ksm(308495997-1,mod-2));
    //F(n) = √5/5[((1+√5)/2)^n-((1-√5)/2)^n]
    //383008016^2 ≡ 5 (mod 1e9 + 9)
    //383008016 ≡ sqrt(5) (mod 1e9 + 9)
    //printf("%lld\n", ksm(383008016,mod-2));//1/sqrt(5)≡276601605(mod)
    //printf("%lld\n", 383008017*ksm(2,mod-2)%mod);//(1+sqrt(5))/2≡691504013(mod)
    //printf("%lld\n", (mod-383008016+1)*ksm(2,mod-2)%mod);//(1-sqrt(5))/2≡308495997(mod)
    scanf("%d%d", &n, &m);
    mul1[0] = mul2[0] = 1;
    for(int i = 1; i < 301000; ++i) {
        mul1[i] = mul1[i-1] * p1;
        mul2[i] = mul2[i-1] * p2;
        check(mul1[i]); check(mul2[i]);
    }
    for(int i = 1; i <= n; ++i) scanf("%lld", &ar[i]), pre[i] = (pre[i-1] + ar[i])%mod;
    while(m --) {
        int opt, l, r;
        scanf("%d%d%d", &opt, &l, &r);
        if(opt == 1) {
            update(l, r, 1, n, 1, 1, 1);
        }else {
            printf("%lld\n", ((p3*query(l,r,1,n,1)%mod+pre[r]-pre[l-1])%mod+mod)%mod);
        }
    }
    return 0;
}

（二）

斐波纳契数列的一些性质：



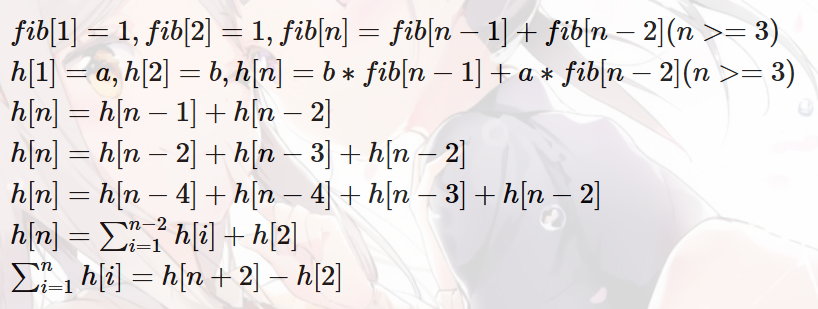
性质1：对于一个满足斐波那契性质的数列，如果我们已知它的前两项，我们可以O(1)的得到它的任意一项和任意前缀和！

性质2：两个满足斐波那契性质的数列相加后，依然是斐波那契数列。前两项的值分别为两个的和。

所以本题我们用线段树的\(lazy\)标记维护给这个区间各项加上的\(fib\)数列的前两项的值。通过这个\(lazy\)标记我们可以\(O(1)\)更新区间和，因为斐波纳契数列满足可加性，所以我们\(lazy\)标记也可以很轻松的\(push\_down\)操作。代码如下。

#include<bits/stdc++.h>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;

const int MXN = 5e5 + 6;
const int INF = 0x3f3f3f3f;
const LL mod = 1000000009;
const LL p1 = 691504013;
const LL p2 = 308495997;
const LL p3 = 276601605;

int n, m;
LL ar[MXN], fib[MXN];
LL sum[MXN<<2], lazy1[MXN<<2], lazy2[MXN<<2];
LL ksm(LL a, LL b) {
    LL res = 1;
    for(;b;b>>=1,a=a*a%mod) {
        if(b&1) res = res * a %mod;
    }
    return res;
}
LL hn(int n,LL a,LL b) {
    if(n == 1) return (a%mod+mod)%mod;
    if(n == 2) return (b%mod+mod)%mod;
    return ((a*fib[n-2] + b*fib[n-1])%mod+mod)%mod;
}
void check(LL &a) {
    if(a >= mod) a %= mod;
}
void push_up(int rt) {
    sum[rt] = sum[lson] + sum[rson]; check(sum[rt]);
}
void build(int l,int r,int rt) {
    if(l == r) {
        sum[rt] = ar[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(l, mid, lson); build(mid+1, r, rson);
    push_up(rt);
}
void push_down(int l,int r,int rt) {
    if(lazy1[rt] == 0 && lazy2[rt] == 0) return;
    LL a = lazy1[rt], b = lazy2[rt];
    int mid = (l + r) >> 1;
    int len1 = mid-l+1, len2 = r - mid;
    lazy1[lson] += a; lazy2[lson] += b;
    sum[lson] = (sum[lson] + hn(len1+2,a,b) - b)%mod+mod;
    lazy1[rson] += hn(len1+1,a,b); lazy2[rson] += hn(len1+2,a,b);
    sum[rson] = (sum[rson] + hn(len2+2,hn(len1+1,a,b),hn(len1+2,a,b))-hn(len1+2,a,b))%mod+mod;
    check(sum[lson]); check(sum[rson]);
    check(lazy1[lson]);check(lazy1[rson]);check(lazy2[lson]);check(lazy2[rson]);
    lazy1[rt] = lazy2[rt] = 0;
}
void update(int L,int R,int l,int r,int rt,LL x, LL y) {
    if(L <= l && r <= R) {
        lazy1[rt] += x; lazy2[rt] += y;
        check(lazy1[rt]); check(lazy2[rt]);
        sum[rt] = (sum[rt] + hn(r-l+1+2,x,y) - y)%mod+mod; check(sum[rt]);
        return;
    }
    push_down(l, r, rt);
    int mid = (l + r) >> 1;
    if(L > mid) update(L,R,mid+1,r,rson,x,y);
    else if(R <= mid) update(L,R,l,mid,lson,x,y);
    else {
        update(L,mid,l,mid,lson,x,y);
        update(mid+1,R,mid+1,r,rson,hn(mid-L+1+1,x,y), hn(mid-L+1+2,x,y));
    }
    push_up(rt);
}
LL query(int L,int R,int l,int r,int rt) {
    if(L <= l && r <= R) {
        return sum[rt];
    }
    push_down(l,r,rt);
    int mid = (l+r) >> 1;
    if(L > mid) return query(L,R,mid+1,r,rson);
    else if(R <= mid) return query(L,R,l,mid,lson);
    else {
        LL ans = query(L,mid,l,mid,lson);
        ans += query(mid+1,R,mid+1,r,rson);
        check(ans);
        return ans;
    }
}
int main() {
    scanf("%d%d", &n, &m);
    fib[1] = fib[2] = 1;
    for(int i = 3; i < 301000; ++i) {
        fib[i] = fib[i-1] + fib[i-2];
        check(fib[i]);
    }
    for(int i = 1; i <= n; ++i) scanf("%lld", &ar[i]);
    build(1, n, 1);
    while(m --) {
        int opt, l, r;
        scanf("%d%d%d", &opt, &l, &r);
        if(opt == 1) {
            update(l, r, 1, n, 1, 1, 1);
        }else {
            printf("%lld\n", query(l,r,1,n,1));
        }
    }
    return 0;
}