二分优化lis和STL函数

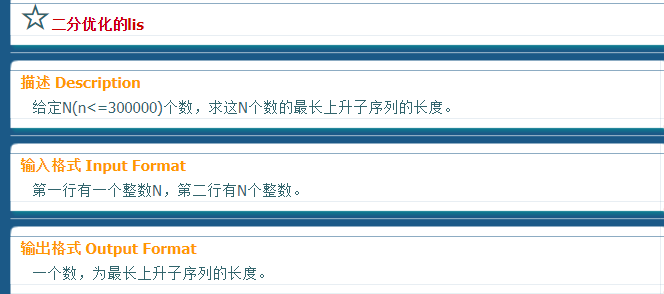
LIS：最长上升子序列；

这个题我们很显然会想到使用dp，

状态设计：dp[i]代表以a[i]结尾的LIS的长度 
状态转移：dp[i]=max(dp[i], dp[j]+1) (0<=j< i, a[j]< a[i]) 
边界处理：dp[i]=1 (0<=j< n) 
时间复杂度：O(N^2) 

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
    int x=,f=;  char ch=getchar();
    while(!isdigit(ch))  {if(ch=='-')  f=-;  ch=getchar();}
    while(isdigit(ch))  {x=x*+ch-'';  ch=getchar();}
    return x*f;
}
using namespace std;
const int MAXN=;
int n,a[MAXN],dp[MAXN];
int LIS()
{
    int ans=;
    for(int i=;i<=n;i++)
    {
        dp[i]=;
        for(int j=;j<i;j++)
        if(a[i]>a[j])    dp[i]=max(dp[i],dp[j]+);
        ans=max(ans,dp[i]);
    }
    return ans;
}
int main()
{
       n=read();
    for(int i=; i<=n; i++)
        cin>>a[i];
    int ans=LIS();
    cout<<ans<<endl;
    return ;
}

但是n^2的做法显然会超时，所以介绍一种二分优化的做法；

用二分+贪心的思想可以将时间复杂度优化至（nlogn);

a[i]表示第i个原数据。 
dp[i]表示表示长度为i+1的LIS结尾元素的最小值。 
利用贪心的思想，对于一个上升子序列，当前添加的最后一个元素越小，越有利于添加新的元素，这样LIS长度更长。 
因此，我们只需要维护dp数组，其表示的就是长度为i+1的LIS结尾元素的最小值，保证每一位都是最小值，

这样子dp数组的长度就是LIS的长度。

这样每次查找就用到了我们的stl函数撒；

介绍一下upper_bound和lower_bound；

（刚知道这个东西）

lower_bound( )和upper_bound( )是利用二分查找的方法在一个有序的数组中进行查找的。

当数组是从小到大时，

lower_bound( begin,end,num)：表示从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,找到数字在数组中的下标。

upper_bound( begin,end,num)：表示从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,找到数字在数组中的下标。

当数组是从大到小时，我们需要重载lower_bound()和upper_bound()；

struct cmp{bool operator()(int a,int b){return a>b;}};

lower_bound( begin,end,num,cmp() ):从数组的begin位置到end-1位置二分查找第一个小于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound( begin,end,num,cmp() ):从数组的begin位置到end-1位置二分查找第一个小于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

所以我们就可以使用stl函数寻找lis啦；

针对上面那个题：

#include<bits/stdc++.h>
using namespace std;
#define N 500001
inline int read()
{
    int x=,f=;  char ch=getchar();
    while(!isdigit(ch))  {if(ch=='-')  f=-;  ch=getchar();}
    while(isdigit(ch))  {x=x*+ch-'';  ch=getchar();}
    return x*f;
}
int n,a[N],l[N];
struct cmp{bool operator()(int a,int b){return a>b;}};
int main()
{
    n=read();
    for(int i=;i<=n;i++)    a[i]=read();
    int con=,cont=;
    l[]=a[];
    for(int i=;i<=n;i++)
    {
        if(l[cont]<a[i])    l[++cont]=a[i];
        else l[upper_bound(l+,l+cont+,a[i])-l]=a[i];
    }
    cout<<cont<<endl;
    return ;
}
    

所以我们想一下有没有什么dp的题可以用stl写呢？

嗯...导弹拦截，这个题可以完美的体现stl的好处；

luogu；

这个题我们需要求出最长单调不升子序列和一个最长单调上升子序列；

这个题两种写法，学了stl后又写了一个，明显stl代码短很多；

因为洛谷输入和本校oj不太一样，酌情修改代码...

#include<bits/stdc++.h>
using namespace std;
int a[],f[],l[],n;
struct cmp{bool operator()(int a,int b){return a>b;}};
int main()
{
//    int n=1;
//    while(cin>>a[n])    n++;
//    n--;
    cin>>n;
    for(int i=;i<=n;i++)    cin>>a[i];
    int con=,cont=;
    l[]=f[]=a[];
    for(int i=;i<=n;i++)
    {
        if(l[cont]>=a[i])l[++cont]=a[i];
        else l[upper_bound(l+,l+cont+,a[i],cmp())-l]=a[i];
        if(f[con]<a[i])f[++con]=a[i];
        else f[lower_bound(f+,f+con+,a[i])-f]=a[i];
    }
    cout<<cont<<endl<<con;
    return ;
}
/*
#include<iostream>
using namespace std;
int n;
int h[1001],ht[1001],best[1001];
int ans=0;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
       cin>>h[i];
    best[0]=0x7fffffff;
    for(int i=1;i<=n;i++)
        for(int j=ans;j>=0;j--)
           if(best[j]>=h[i])
           {
                   best[j+1]=h[i];
                ans=max(ans,j+1);
                break;
            }
    cout<<ans<<endl;
    ans=0;
    for(int i=1;i<=n;i++)
    {
       for(int j=0;j<=ans;j++)
          {
               if(ht[j]>=h[i])
            {
                       ht[j]=h[i];
                    break;
            }
          }
          if(ht[ans]<h[i])ht[++ans]=h[i];
    }
    cout<<ans;
    return 0;
}*/

看了好多手写二分的都快一二百行了，可是我还不会啊...

所以懒，写了stl函数，才知道代码的精短，核心不到十行；

总结：寻找最长上升（使用lower_bound）和最长不下降时（使用upper_bound），无需重载；

寻找最长下降（使用lower_bound）和最长不上升时（使用upper_bound），需重载；

#include<bits/stdc++.h>
using namespace std;
const int N=7e5+;
template<typename T>inline void read(T &x)
{
    x=;T f=,ch=getchar();
    while(!isdigit(ch))  {if(ch=='-')  f=-;  ch=getchar();}
    while(isdigit(ch))  {x=x*+ch-'';  ch=getchar();}
    x*=f;
}
long long n,f[N],s[N],t[N],l[N],a[N],ans1,ans2,ans3,ans4;
struct cmp{bool operator()(int a,int b){return a>b;}};
int main()
{
    read(n);
    for(int i=;i<=n;i++)
        read(a[i]);
    l[]=f[]=s[]=t[]=a[];
    ans1=ans2=ans3=ans4=;
    for(int i=;i<=n;i++)
    {
        if(f[ans1]<a[i]) f[++ans1]=a[i];
        else f[lower_bound(f+,f+ans1+,a[i])-f]=a[i];
        if(s[ans2]>a[i]) s[++ans2]=a[i];
        else s[lower_bound(s+,s+ans2+,a[i],cmp())-s]=a[i];
        if(t[ans3]>=a[i]) t[++ans3]=a[i];
        else t[upper_bound(t+,t+ans3+,a[i],cmp())-t]=a[i];
        if(l[ans4]<=a[i]) l[++ans4]=a[i];
        else l[upper_bound(l+,l+ans4+,a[i])-l]=a[i];
    }
    printf("%lld\n%lld\n%lld\n%lld\n",ans1,ans2,ans3,ans4);
    return ;
}