论文翻译：Neural Networks With Few Multiplications

Abstract
1. Introduction
2.Related Work
3.Binary And Ternary Connect
- 3.1 BINARY CONNECT REVISITED
- 3.2 Ternary Connect
4.Quantized Back Propagation
5.Experiments
6.Conclusion And Future Work
参考资料

论文地址：https://arxiv.org/pdf/1510.03009.pdf

Abstract

众所周知，对于大多数深度学习算法而言，训练是非常耗时的。由于训练神经网络中的大多数计算通常用于浮点数乘法，我们研究了一种可以减少或消除这些乘法的训练方法。我们的方法由两部分组成：首先我们随机地二值化权重，以转换计算隐藏状态涉及符号变化的乘法。其次，在反向传播误差导数的同时，除了对权重进行二值化之外，我们还量化每层的表示以将剩余的乘法转换为二进制移位。在3个流行数据集（MNIST，CIFAR10，SVHN）的实验结果表明，这种方法不仅如此不会损害分类性能，而且还可以产生比标准随机梯度下降法训练更好的效果，为快速、硬件友好的神经网络训练铺平了道路。

1. Introduction

训练深度神经网络长期以来一直是需求高强度计算且耗费时间。对于一些最先进的架构，可能需要数周的时间来训练模型（Krizhevsky等，2012）。另一个问题是对内存的需求可能很巨大。例如，在语音识别或机器翻译中的许多常见模型需要12GB或更多的存储空间（Gulcehre等，2015）。为了解决这些问题，通常采用GPU或CPU集群以及精心设计的并行化策略来训练深度神经网络（Le，2013）。

在训练神经网络中执行的大多数计算是浮点数乘法。在本文中，我们专注于消除大多数这些乘法以减少计算。基于我们以前的工作（Courbariaux等，2015），它通过二值化权重来消除计算隐藏层表示的乘法，我们的方法处理隐藏层状态计算和反向权重更新。我们的方法有2个部分。在前向传递中，使用我们称为二值化连接或三值化连接的方法对权重进行随机二值化，并且对于误差的反向传播，我们提出了一种新方法，我们将其称为量化反向传播，将乘法转换为移位操作。

2.Related Work

过去已经提出了几种方法来简化神经网络中的计算。 他们中的一些人试图将权重值限制为2的整数幂，从而将所有乘法减少为二进制移位（Kwan＆Tang，1993; Marchesi等，1993）。通过这种方式，在训练和测试时间中消除了乘法。缺点是可以严重降低模型性能，并且不再能保证训练的收敛。

Kim＆Paris（2015）引入了一个全布尔值的网络，它以可接受的性能表现简化了测试时间计算。该方法仍然需要全精度的实值，然而减少计算的好处并不能应用于训练。同样，Machado等人(2015）设法在稀疏表示分类上通过整数移位替换所有浮点乘法，来获得可接受的准确性。比特流网络（Burgeet al，1999）也提供了一种通过用逻辑门替换权重连接来二值化神经网络。与此类似，Cheng等人（2015）证明用期望反向传播中，具有二值化权重的深度神经网络可以训练来区分多个类别。

还有一些其他技术，专注于降低训练的复杂性。例如，SimardGraf（1994）不是降低权重的精确度，而是将状态，学习率和梯度量化为2的幂。这种方法设法消除乘法，而性能降低可忽略不计。

3.Binary And Ternary Connect

3.1 BINARY CONNECT REVISITED

在我们上一个工作中（2015），引入了一种权重二值化技术，它消除了前向传播中的乘法。我们在本小节中总结了这种方法，并在接下来引入其拓展方法。

考虑到一个神经网络层具有N个输入和M个输出单元。前向传播计算是y =h（Wx + b）其中W和b分别是权重和偏差，h是激活函数，x和y是层的输入和输出。如果我们选择ReLU作为h，则在计算激活函数值时将不存在乘法，因此所有乘法都存在于矩阵乘积Wx中。对于每个输入向量x，需要N*M次浮点数乘法。

二值化连接通过随机抽样权重为-1或1来消除这些乘法。全精度权重w作为参考保存在内存中，每次需要y时，我们根据w采样随机权重矩阵W。对于采样矩阵W的每个元素，获得1的概率与其中相应的w“接近”1的程度成正比。即(w_ij为正取1，w_ij为负取-1)，

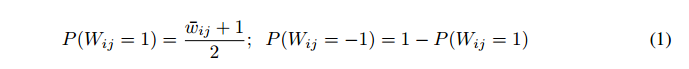
有必要为w添加一些边缘约束。为了确保P(W_ij = 1)处于合理的范围内，w中的值被强制为区间[-1,1]中的实数值。如果在更新期间其任何值超出该间隔，我们将其设置为其对应的边值-1或1。这样，浮点乘法变为符号变化。

剩下的问题涉及在采样过程中涉及的随机数生成器中乘法的使用。对于算法来说，采样整数必须比乘法更快。确切地说，在大多数情况下，我们只做小批量学习，并且对整个小批量只进行一次采样过程。通常，批量大小B可达数百。因此，只要一个采样过程明显快于B次乘法，这仍然是值得去做的。幸运的是，Jeavons已经研究了有效生成随机数等（1994）; van Daalen等（1993）。此外，可以根据实际随机过程（如CPU温度等）获取随机数。我们不会详细介绍随机数生成，因为这不是本文的重点。

3.2 Ternary Connect

在前一小节中引入的二值化连接允许权重为-1或1。然而，在一个已训练的神经网络中，通常观察到许多学习的权重为零或接近于零。虽然随机抽样过程允许抽样权重的平均值为零，但这表明明确允许权重为零可能是有益的。

为了使权重为零，需要对方程1进行一些调整。我们将[-1,1]的区间分成两个子区间：[-1, 0]和(0, 1]，其中全精度权重值w_ij位于其中。如果一个权重值w_ij落入其中一个，我们根据它们与w_ij的距离，将w_ij作为该区间的两个边缘值进行采样。

若w_ij > 0:

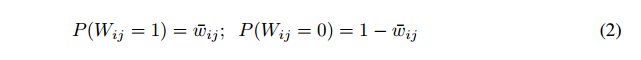
若w_ij <= 0:

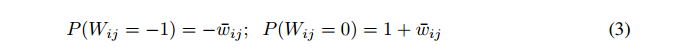
与二值化连接一样，三值化连接也消除了正向传递中的所有乘法。

4.Quantized Back Propagation

在前一节中，我们描述了如何从前向传播中消除乘法。在本节中，我们提出了一种反向传播消除乘法的方法。

假设网络的第i层具有N个输入和M个输出单元，并考虑从其输出向下传播的误差符号δ。权重和偏重的更新将是网络层输入和误差符号的外积：

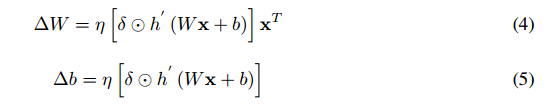
其中η是学习率，x是层的输入。运算符代表元素乘法。在通过层传播时，也需要更新误差符号δ。其更新考虑到下面的下一层采用以下形式：

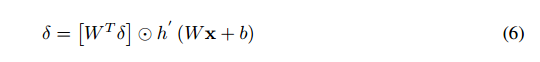
在等式4-6中有3个术语反复出现：δ、h'（Wx + b）和x。后两个术语引入矩阵外积。 为了消除乘法，我们可以将其中一个量化为2的整数次幂，因此涉及该项的乘法变为二进制移位。 表达式h'（Wx + b）包含向下流动的梯度，其主要由loss函数和网络参数决定，因此很难绑定其值。然而，限制值对于量化是必不可少的，因为我们需要为每个采样值提供固定数量的位，如果该值变化太大，我们将需要太多位用于指数化。反过来，这将导致需要更多的比特来存储采样值并且会不必要地增加所需的计算量。

虽然h'（Wx + b）不是量化的好选择，但x是更好的选择，因为它是每层的隐藏输出，我们大致知道每层激活的分布。

因此，我们的方法是通过将x中的每个条目量化为2的整数幂消除方程式4中的乘法。这样，方程式4中的外积成为一系列的位移。在实验上，我们发现允许最多3到4位的移位足以使网络运行良好。这意味着3位已足以量化x。由于float32格式具有24位尾数，因此可以完全容忍（向左或向右）移位3到4位。我们将这种反向传播方法称为“量化反向传播”。

如果我们选择ReLU作为激活函数，由于我们正在重用在前向传递期间计算的（Wx + b），计算式h'（Wx + b）不涉及额外的采样或乘法。此外，量化反向传播消除了等式4中外积的乘法。唯一存在乘法的地方是元素乘积。在等式5，乘以η和σ需要2×M次乘法，而在等式4，我们可以重用等式5的结果。为更新δ将需要另外的M次乘法，因此对于来自等式4-6的所有计算需要3×M次乘法。算法1中的伪代码概述了量化反向传播的方式：

与前向传递一样，大多数乘法都用于权重更新。与标准反向传播相比，其至少需要2MN + 3M次乘法，在量化反向传播中剩余的乘法量可以忽略不计。我们在第5节中的实验表明，这种显着减少乘法的方法并不一定会导致性能上损失。

5.Experiments

我们在完全连接的网络和卷积网络上尝试了我们的方法。我们使用Theano做实验（Bastien等，2012）。我们试验了3个数据集：MNIST，CIFAR10和SVHN。在下面的小节中，我们将展示这些轻量乘法器神经网络可以实现的性能。在随后的小节中，我们将更详细地研究它们的一些属性，例如收敛性和鲁棒性。

5.1 General Performance

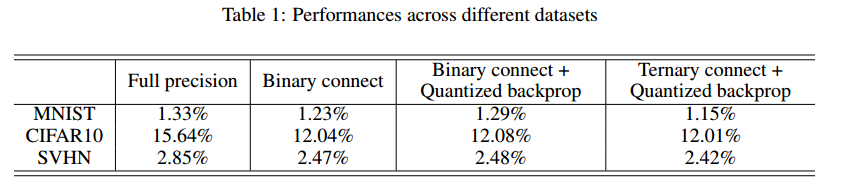
我们测试了我们方法的不同变种，并将结果与Courbariaux等（2015）和全精度训练（表1）进行了比较。所有模型都采用没有动量的随机梯度下降训练（SGD）。我们对所有模型使用批量标准化来加速学习。在训练时，使用二值化（三元）连接和量化反向传播，在测试时我们使用学习的全精度权重进行前向传播。对于每个数据集，除了学习速率适合每一种方法之外，所有超参数都为不同方法设置的相同值。

5.1.1 MNIST

MNIST数据集（LeCun等，1998）有50000个用于训练的图像和10000个用于测试的图像。所有图像都是尺寸为28×28像素的灰色图像，分为10个类，对应于10个数字。 我们使用的模型是一个4层全连接的网络：784-1024-1024-1024-10。在最后一层，我们使用hinge loss作为损失函数。 训练集分为两部分，其中一部分是具有40000个图像的训练集，另一部分是具有10000个图像的验证集。训练以小批量大小为200的方式进行。

在三值化连接，量化反向传播和批量归一化的情况下，我们的错误率达到1.15％。该结果优于全精度训练（也具有批量归一化），其产生1.33％的错误率。如果没有批量归一化，错误率分别上升到1.48％和1.67％。在我们在测试时间内对这些权重进行采样，会探索其表现性能。在测试时使用三值化连接，相同的模型（错误率达到1.15％）产生1.49％的错误率，这仍然是可以接受的。我们的实验结果表明，尽管删除了大多数乘法，但我们的方法产生的性能表现与全精度训练相当（实际上甚至略高）。性能提升可能是由于随机抽样所带来的正规化效应。

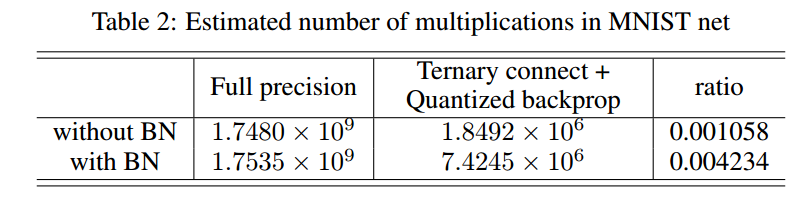
以该网络为例，可以精确估计每种情况下的实际乘法数量。前向传递中的乘法是显而易见的，并且对于反向传播章节4已经给出了估计。现在我们估计批量标准化产生的乘法数量。假设我们在具有M个输出单元的层上具有预先隐藏的表示层h，其小批量大小为B（因此h应该具有形状B×M），然后批量归一化公式化为：

需要计算小批量的mean（h），其采用M次乘法，并且需要BM + 2M次乘法计算标准偏差std（h）。该分数采用BM次除法，它应该等同于相同数量的乘法。乘以γ参数，再加上BM次乘法。因此，每个批量归一化层在前向传播中需要额外的3BM + 3M次乘法。如果我们使用SGD，反向传播大约需要两倍的乘法。无论我们是否使用二值化，这些乘法量都是相同的。考虑到这一点，表2中显示了在小批量更新中调用的乘法总数。最后一列列出了在应用三值化连接和量化反向传播之后剩余乘法量占比。

5.1.2 CIFAR10

CIFAR10（Krizhevsky＆Hinton，2009）包含大小为32×32 RGB像素的图像。与MNIST一样，我们将数据集分别分为40000,10000和10000个训练，验证和测试用例。我们将方法应用于在这些数据集训练卷积神经网络。该网络有6个卷积/池化层，1个全连接层和1个分类层。我们使用hinge loss进行训练，批量大小为100。我们还尝试在测试时使用三元连接。当使用三值化连接和量化反向传播训练的模型时，它产生13.54％的错误率。与我们在完连接的网络中观察到的类似，二值化（三值化）连接和量化反向传播产生比普通SGD略高的性能。

5.1.3 SVHN

街景房号（SVHN）数据集（Netzer等，2011）包含门牌号的RGB图像。它在扩展的训练集中包含超过600,000张图像，测试集中有26,000张图像。我们从训练集中删除了6,000张图像以进行验证。我们使用7层卷积/池，1个完全连接层和1个分类层。批量大小也是设定为100。我们获得的表现与我们在CIFAR10上的结果一致。将三元连接机制扩展到其测试时间会在此数据集上产生2.99％的错误率。同样，它通过使用二进制（三元）连接和量化反向传播来改进普通SGD。

5.2 Convergence

以CIFAR10上的卷积网络作为试验对象，我们现在更详细地研究学习行为。图1显示了在训练期间测试错误率方面的模型性能。该图显示二值化使网络收敛比普通SGD慢，但在算法收敛后产生更好的结果。与二进化连接（红线）相比，在误差传播中增加量化（黄线）根本不会损害模型精度。此外，三值化连接与量化反向传播（绿线）相结合超过了其他三种方法。

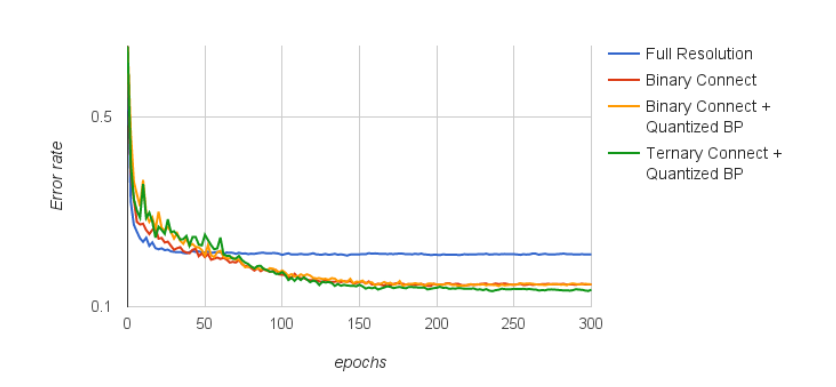
图1：普通反向传播的每个epoch的测试集错误率，二值化连接，具有量化反向传播的二值化连接，以及具有量化反向传播的三值化连接。纵轴以对数标度表示。

5.3 The effect of bit clipping

在第4节中，我们提到量化将受限于我们使用的位数。要移位的最大位数决定了所需的内存量，但它也决定了单个权重更新的变化范围。图2显示了作为最大允许位移的函数的模型性能。这些实验是用上述全连接模型在MNIST数据集上进行的。对于每个位裁剪的情况，我们用不同的初始随机实例重复实验10次。

该图显示该方法对使用的位数不是很敏感。图中允许的最大移位从2位到10位不等，性能基本保持不变。即使将位移限制为2，模型仍然可以成功学习。事实上，表现性能对允许的可位移最大值不是很敏感，这表明我们不需要重新定义用于量化不同任务的x的比特数，这将是一个重要的实际优势。

要量化的x不一定是围绕2对称分布的。例如，图3示出了训练中间每层的x分布。左侧的最大偏移量不需要与右侧的偏移量相同。更有效的方法是对最大左移和最大右移使用不同的值。记住这点，我们将其设置为右边最多3位，左边4位。

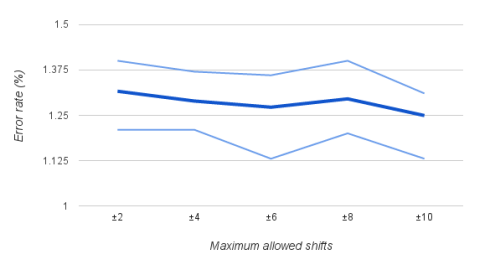
图2：量化反向传播中允许的最大位移函数的模型性能。深蓝色线表示10次独立运行的平均错误率，而浅蓝色线表示其相应的最大和最小错误率。

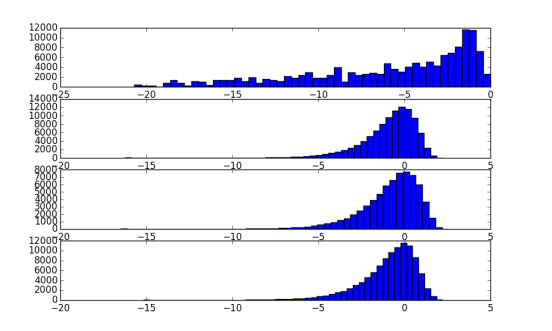
图3：为MNIST训练全连接的网络时每层的表示直方图。该图代表了训练中期的快照。每个子图从下到上表示从第一层到最后一层的隐藏状态的直方图。水平轴代表层表示的指数值，即log₂ x。

6.Conclusion And Future Work

我们提出了一种方法来消除在训练前馈神经网络时使用的大多数浮点数乘法。这可以大大加快训练神经网络的速度通过使用专用硬件实现。

一个有点令人惊讶的事实是，该方法不会降低预测准确性，甚至可以提高，这可能是由于以下几个原因：首先是随机抽样过程引起的正则化效应。通过对权重值进行采样而产生的噪声注入可以被视为正则化器，这可以提高模型的泛化能力。第二个原因是低精度重量值。基本上，神经网络的泛化误差界限取决于权重精度。低精度阻止优化器找到需要大量精度的解决方案，这些解决方案对应于非常稀疏（高曲率）的临界点，并且这些最小值更可能对应于过拟合的解决方案，然后是广泛的最小值（有更多的功能可以和解决方案兼容，对应于更好的描述长度并因此具有更好地泛化能力）。

同样，Neelakantan等人（2015）将噪声添加到梯度中，这使得优化器更偏爱在large-basin区域并迫使它找到全局的最小值。它还可以降低训练loss并提高器泛化能力。

未来工作的方向包括探索这种方法的实际实现（例如，使用FPGA），寻求更有效的二值化方法，以及对递归神经网络的扩展。

参考资料

谷歌翻译

本人根据谷歌翻译组织整理语句，英语水平有限，翻译错误望指正