R语言之Apriori算法

---恢复内容开始---

1.概念

关联分析：用于发现隐藏在大型数据集中的有意义的联系

项集：0或多个项的集合。例如:{啤酒，尿布，牛奶，花生} 是一个4-项集，意义想象成爸爸去超市买啤酒和花生，给儿子和老婆分别买尿布和牛奶。

关联规则：啤酒->花生，其强度可用支持度和置信度来度量

支持度：一个项集或者规则在所有事物中出现的频率，即此规则能否普遍运用于给定数据集。σ(X):表示项集X的支持度计数，项集X的支持度：s(X)=σ(X)/N；规则X → Y的支持度：s(X → Y) = σ(X∪Y) / N

置信度：确定Y在包含X的事务中出现的频繁程度。c(X → Y) = σ(X∪Y)/σ(X)

支持度是用来判断规则有没有意义，删去无意义规则；置信度度量是通过规则进行推理具有可靠性。对于给定的规则X → Y，置信度越高，Y在包含X的事物中出现的可能性就越大。即Y在给定X下的条件概率P(Y|X)越大。

2.Groceries是arules包自带的超市经营一个月的购物数据，含9835次交易，9835次/30天/12小时/天=27.3笔/小时->此超市属于中型超市

2.1数据源

2.2探索和准备数据

1 inspect(Groceries[1:5])   #通过inspect函数查看Groceries数据集的前5次交易记录
2 itemFrequency(Groceries[,1:3])   #itemFrequency()函数可以查看商品的交易比例<br>frankfurter sausage liver loaf <br>0.058973055 0.093950178 0.005083884
3 summary(Groceries)

交易比例

总体情况

2.3可视化商品的支持度——商品的频率图

为了直观地呈现统计数据，可以使用itemFrequenctyPlot()函数生成一个用于描绘所包含的特定商品的交易比例的柱状图。因为包含很多种商品，不可能同时展现出来，因此可以通过support或者topN参数进行排除一部分商品进行展示

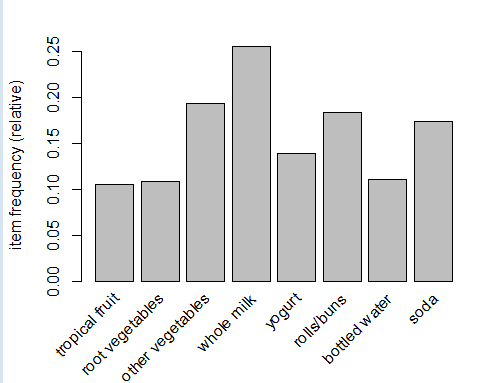
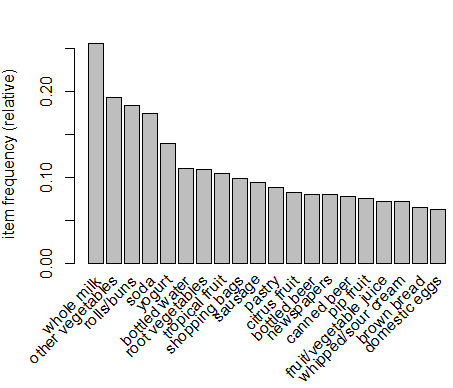
> itemFrequencyPlot(Groceries,support = 0.1)  # support = 0.1 表示支持度至少为0.1

> itemFrequencyPlot(Groceries,topN = 20)  # topN = 20 表示支持度排在前20的商品

2.4可视化交易数据，绘制稀疏矩阵

 image(Groceries[:]) # 生成一个5行169列的矩阵，矩阵中填充有黑色的单元表示在此次交易（行）中，该商品（列）被购买了

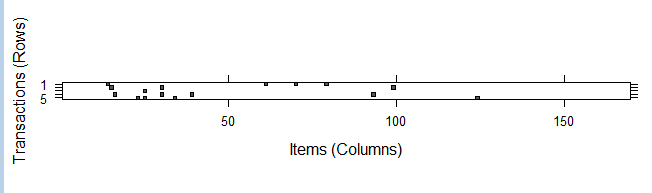
从上图可以看出，第一行记录（交易）包含了四种商品（黑色的方块），这种可视化的图是用于数据探索的一种很有用的工具。它可能有助于识别潜在的数据问题，比如：由于列表示的是商品名称，如果列从上往下一直被填充表明这个商品在每一次交易中都被购买了；另一方面，图中的模式可能有助于揭示交易或者商品的有趣部分，特别是当数据以有趣的方式排序后，比如，如果交易按照日期进行排序，那么黑色方块图案可能会揭示人们购买商品的数量或者类型受季节性的影响。这种可视化对于超大型的交易数据集是没有意义的，因为单元太小会很难发现有趣的模式。

2.5训练模型

 grocery_rules <- apriori(data=Groceries,parameter=list(support =0.1,confidence =0.8,minlen =))

support=0.1意味着商品至少出现在9835*0.1=983.5次交易中（所有买的人中必须有983.5个人购买），在前面的分析中，我们发现只有8种商品的 support >= 0.1,因此使用默认的设置没有产生任何规则也不足为奇。

minlen = 2 表示规则中至少包含两种商品，这可以防止仅仅是由于某种商品被频繁购买而创建的无用规则，比如在上面的分析中，我们发现whole milk出现的概率（支持度）为25.6%，很可能出现如下规则：{}=>whole milk，这种规则是没有意义的。

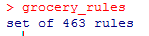
 > grocery_rules=apriori(data=Groceries,parameter=list(support=0.006,confidence=0.25,minlen=))#此时支持度取我们认为的最小交易数量9835*0.006=60次/月，置信度为25%，
即规则正确率至少为25%，排除了最不可靠的规则

结果如下，创建了463项规则

2.6评估性能

 > summary(grocery_rules)
 set of  rules

 rule length distribution (lhs + rhs):sizes #前件+后件的规则分布

      #有150个规则包含2件商品，297个规则包含3件商品，16个规则包含4件商品

    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
   2.000   2.000   3.000   2.711   3.000   4.000 

 summary of quality measures:
     support           confidence          lift            count
  Min.   :0.006101   Min.   :0.2500   Min.   :0.9932   Min.   : 60.0
  1st Qu.:0.007117   1st Qu.:0.2971   1st Qu.:1.6229   1st Qu.: 70.0
  Median :0.008744   Median :0.3554   Median :1.9332   Median : 86.0
  Mean   :0.011539   Mean   :0.3786   Mean   :2.0351   Mean   :113.5
  3rd Qu.:0.012303   3rd Qu.:0.4495   3rd Qu.:2.3565   3rd Qu.:121.0
  Max.   :0.074835   Max.   :0.6600   Max.   :3.9565   Max.   :736.0  

 mining info:
       data ntransactions support confidence
  Groceries             0.006       0.25

lift（提升度）：相对于一般购买率，受前件影响之后，后件的购买率提升了多少，规则解读见如下：

1 > inspect(grocery_rules[1:5])
     lhs             rhs                support     confidence lift     count
 [] {pot plants} => {whole milk}       0.006914082 0.4000000  1.565460    
 [] {pasta}      => {whole milk}       0.006100661 0.4054054  1.586614
 [] {herbs}      => {root vegetables}  0.007015760 0.4312500  3.956477
 [] {herbs}      => {other vegetables} 0.007727504 0.4750000  2.454874
 [] {herbs}      => {whole milk}       0.007727504 0.4750000  1.858983  

第一条规则解读：

规则：{plot plants}->{whole milk}某顾客买了pot plants后还会购买whole milk； 支持度：该规则涵盖了0.7%的交易； 置信度：此规则发生的概率是40%;  提升度：相比于单买whole milk,买plot plants后再购买whole miik的可能性提升了1.565倍；1.56=40%的概率/25.6%的顾客，算出来一致

lift>1说明商品一起购买比单买更常见

2.7提高性能

 （1）对关联规则集合排序

 sort()函数排序，默认降序，decreasing=FALSE反转排序

 > inspect(sort(grocery_rules,by="lift")[1:10])
      lhs                   rhs                      support confidence     lift count
 []  {herbs}            => {root vegetables}    0.007015760  0.4312500 3.956477
 []  {berries}          => {whipped/sour cream} 0.009049314  0.2721713 3.796886
 []  {tropical fruit,
       other vegetables,
       whole milk}       => {root vegetables}    0.007015760  0.4107143 3.768074
 []  {beef,
       other vegetables} => {root vegetables}    0.007930859  0.4020619 3.688692
 []  {tropical fruit,
       other vegetables} => {pip fruit}          0.009456024  0.2634561 3.482649
 []  {beef,
       whole milk}       => {root vegetables}    0.008032537  0.3779904 3.467851
 []  {pip fruit,
       other vegetables} => {tropical fruit}     0.009456024  0.3618677 3.448613
 []  {pip fruit,
       yogurt}           => {tropical fruit}     0.006405694  0.3559322 3.392048
 []  {citrus fruit,
       other vegetables} => {root vegetables}    0.010371124  0.3591549 3.295045
 [] {other vegetables,
       whole milk,
       yogurt}           => {tropical fruit}     0.007625826  0.3424658 3.263712    

 （2）提取关联规则的子集：可以通过subset()函数提取我们感兴趣的规则

 

1 >fruit_rules <- subset(grocery_rules,items %in% "pip fruit")  # items 表明与出现在规则的任何位置的项进行匹配，为了将子集限制到匹配只发生在左侧或者右侧位置上，可以使用lhs或者rhs代替
2 > inspect(sort(fruit_rules,by="lift")[1:5])
    lhs                                  rhs               support     confidence lift     count
[1] {tropical fruit,other vegetables} => {pip fruit}       0.009456024 0.2634561  3.482649 93   
[2] {pip fruit,other vegetables}      => {tropical fruit}  0.009456024 0.3618677  3.448613 93   
[3] {pip fruit,yogurt}                => {tropical fruit}  0.006405694 0.3559322  3.392048 63   
[4] {pip fruit,other vegetables}      => {root vegetables} 0.008134215 0.3112840  2.855857 80   
[5] {pip fruit,whole milk}            => {root vegetables} 0.008947636 0.2972973  2.727536 88   

 > fruit_rules1=subset(grocery_rules,rhs%in%"pip fruit")
 > inspect(fruit_rules1)
     lhs                                  rhs         support     confidence lift     count
 [] {tropical fruit,other vegetables} => {pip fruit} 0.009456024 0.2634561  3.482649