时间复杂度O()与KMP算法

要得到某个结果，可以有很多种方式，算法就是为了寻找一条最快的方式。

而评判其好坏的标准就是时间复杂度。

O(1):

　　我们把执行一次的时间复杂度定义为O(1)

　　sum = a +b;

　　cout << sum <<endl;

O(n):

　　for(int i = 0; i < n ;++n)

　　{　　

　　　　//do something.

　　}

O(n2):

for(int i = 0; i < n ;++n)

　　{　　

　　　for(int j = 0; j < n ;++n)

　　　　{

　　　　　　//do something.

　　　　}

　　}

我们会碰到这样的需求，从一个主字符串中找到一个子串，首先我们想到的是这种方法：

#include "stdafx.h"
#include<iostream>
#include<string>
using namespace std;

int findString(string S,string T)
{
    int i = 0;
    int j = 0;
    while(i<S.length() && j < T.length())
    {
        if(T[j] == S[i])
        {
            i++;
            j++;
        }
        else
        {
            j=0;
            i = i-j+1;
        }
    }
    if(j = T.length())
    {
        return i-j;
    }
    else
    {
        return -1;
    }
}

void main()
{
    int a = findString("adsfdjfxdf","xdf");
    cout << a <<endl;
    cin.get();
    cin.get();
}

时间复杂度为O(n*m)这个好理解，每比较m次，主字符串位置加1，最坏的情况就是比较n*m次

而实际上，我们不需要这样做，例如如果要在主字符串中找abcd,那每次i可以加4，下次直接从第5个开始比较。这样的时间复杂度是O(n/m*m) = O(n),而实际上我们要找的子串有可能会重复，于是一种更通用的算法就产生了， 克努特一莫里斯一普拉特算法， 简称 KMP 算法。

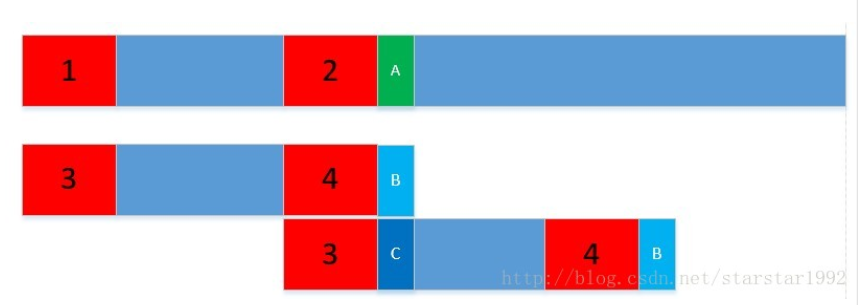
主要思想基于上图，找到的比较便于理解的图，上图中1,2,3,4为相同内容，中间蓝色为相同内容，当我们第一次比较时，发现A和B不同,那么下一次比较时，我们主串仍从A开

始，而子串则从C处开始，3和2相同的内容便不再需要比较。具体解释百度，其实一看就能感觉应该是这样，而i从上次比较失败的地方继续开始在代码上逻辑也不混乱。

因此KMP算法比较关键的便是如何得到子串失败后开始的这个点C,为了得到这个C的位置i,KMP这3个人设计了一个中间数组，来保存子串的若比较失败应该开始的下一个比较点。

next数组, 含义就是一个固定字符串的最长前缀和最长后缀相同的长度。

比如：abcjkdabc，那么这个数组的最长前缀和最长后缀相同必然是abc。

cbcbc，最长前缀和最长后缀相同是cbc。   这个子串的next数组是[0,0,1,2,0]

#include "stdafx.h"
#include<iostream>
#include<string>
using namespace std;

void get_next(string T,int* next)
{
    next[0] = -1;
    int i = 0;
    int j = -1;
    while(i<T.length())
    {
        if((j == (-1)) || (T[i] == T[j]))
        {
            next[++i] = ++j;
        }
        else
        {
            j = next[j];   //可以想象两个子串如上图一样的比较
        }
    }
}

int KMP(string S , string T)
{
    int * next = new int[T.length()+1];
    int i = 0;
    int j = 0;
    get_next(T, next);
    while(i < int(S.length()) && j < int(T.length()))
    {
        if((-1 == j) || S[i] == T[j])
        {
            i++;
            j++;
        }
        else
        {
            j=next[j];      //如上图4区域刚好是next[j]不需要比较，从c处开始比较
        }
    }
    delete []next;
    if(j == T.length())
    {
        return i-j;
    }
    else
    {
        return -1;
    }
}

void main()
{
    string S;
    string T;
    cout<<"please input the Mstring:"<<endl;
    cin>>S;
    cout<<endl<<"please input the Cstring:"<<endl;
    cin >>T;
    cout<<S.length()<<endl;
    cout<<T.length()<<endl;
    cout<<"the child String in the M number is: "<< KMP(S,T);
    system("pause");
}

这个时间复杂度是O(m+n),因为是两个单循环相加。

写这个的时候 while(i < int(S.length()) && j < int(T.length())) 这句没有强转化int,导致j = -1时while循环只执行了一次未继续下去，后来看了一下length返回的并不是int,而是一个抽象的size，被这个错误搞得有点心态崩了。

O(1)