BZOJ 2007: [Noi2010]海拔

2007: [Noi2010]海拔

Time Limit: 20 Sec  Memory Limit: 552 MB
Submit: 2410  Solved: 1142
[Submit][Status][Discuss]

Description

YT市是一个规划良好的城市，城市被东西向和南北向的主干道划分为n×n个区域。简单起见，可以将YT市看作一个

正方形，每一个区域也可看作一个正方形。从而，YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路

（简称道路），每条双向道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2)，城市被划分为2

×2个区域，包括3×3个交叉路口和12条双向道路。 小Z作为该市的市长，他根据统计信息得到了每天上班高峰期

间YT市每条道路两个方向的人流量，即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海

拔高度值，YT市市民认为爬坡是一件非常累的事情，每向上爬h的高度，就需要消耗h的体力。如果是下坡的话，则

不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数)，那么一个人经过这段路

所消耗的体力是max{0, h}（这里max{a, b}表示取a, b两个值中的较大值）。 小Z还测量得到这个城市西北角的交

叉路口海拔为0，东南角的交叉路口海拔为1(如上图所示)，但其它交叉路口的海拔高度都无法得知。小Z想知道在

最理想的情况下（即你可以任意假设其他路口的海拔高度），每天上班高峰期间所有人爬坡所消耗的总体力和的最

小值。

Input

第一行包含一个整数n，含义如上文所示。接下来4n(n + 1)行，每行包含一个非负整数分别表示每一条道路每一个

方向的人流量信息。输入顺序：n(n + 1)个数表示所有从西到东方向的人流量，然后n(n + 1)个数表示所有从北到

南方向的人流量，n(n + 1)个数表示所有从东到西方向的人流量，最后是n(n + 1)个数表示所有从南到北方向的人

流量。对于每一个方向，输入顺序按照起点由北向南，若南北方向相同时由西到东的顺序给出(参见样例输入)。

Output

仅包含一个数，表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和（即总体力和的最小值），结

果四舍五入到整数。

Sample Input

1
1
2
3
4
5
6
7
8

Sample Output

3

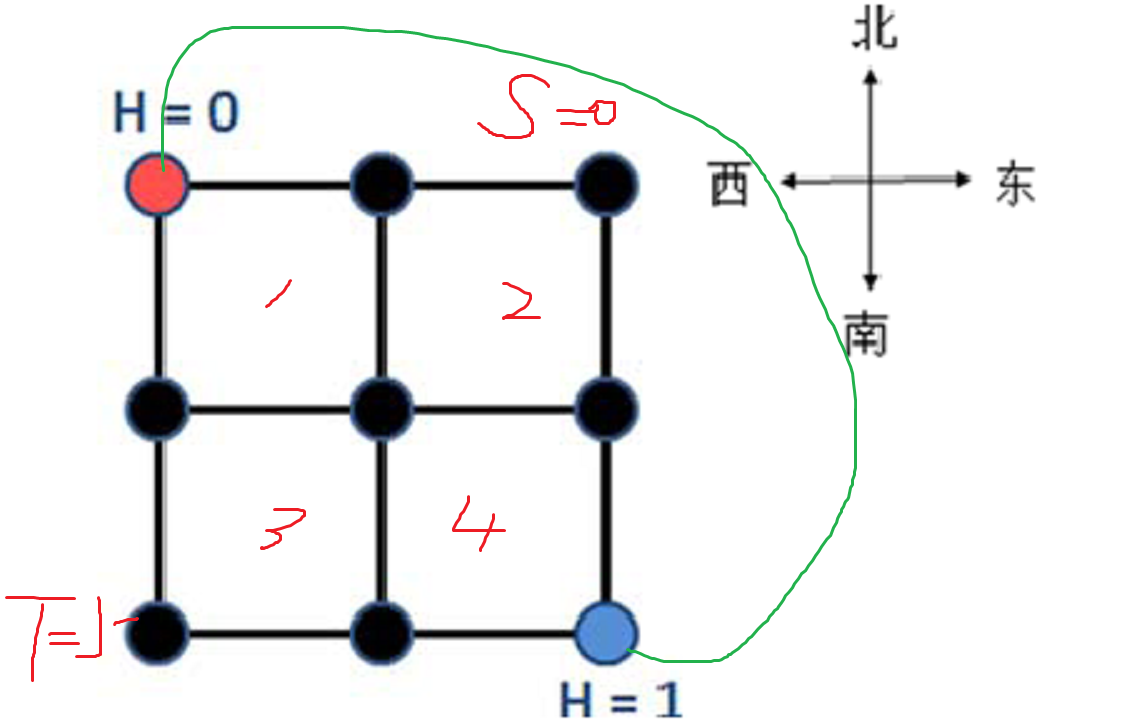
【样例说明】
样例数据见下图。

最理想情况下所有点的海拔如上图所示。
对于100%的数据：1 ≤ n ≤ 500，0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。

HINT

 

Source

 

[Submit][Status][Discuss]

网络流 平面图最小割转对偶图最短路

有个性质，就是一定存在一组最优解，是一些点海拔为0，其余点海拔为1，且两类点各形成一个连通块，即产生代价的边为S到T的一个割边集合，代价即为流量和。

为了防止TLE，最好转对偶图做最短路，注意因为原本是有向边，所以转对偶图时也是有固定规则的有向边。

 #include <queue>
 #include <cstdio>

 inline int nextChar(void) {
     static const int siz = ;
     static char buf[siz];
     static char *hd = buf + siz;
     static char *tl = buf + siz;
     if (hd == tl)
         fread(hd = buf, , siz, stdin);
     return *hd++;
 }

 inline int nextInt(void) {
     register int ret = ;
     register int neg = false;
     register int bit = nextChar();
     for (; bit < ; bit = nextChar())
         if (bit == '-')neg ^= true;
     for (; bit > ; bit = nextChar())
         ret = ret *  + bit - ;
     return neg ? -ret : ret;
 }

 const int inf = 1e9;
 const int siz = ;

 int n;
 int s, t;
 int edges;
 int hd[siz];
 int to[siz];
 int nt[siz];
 int vl[siz];
 int dis[siz];

 inline void add(int u, int v, int w) {
     nt[edges] = hd[u];
     to[edges] = v;
     vl[edges] = w;
     hd[u] = edges++;
 }

 struct pair {
     int x, y;
     pair(void) {};
     pair(int a, int b) :
         x(a), y(b) {};
     inline friend bool operator <
     (const pair &a, const pair &b) {
         return a.x > b.x;
     }
 };

 std::priority_queue<pair> h;

 inline int Dijkstra(void) {
     h.push(pair(dis[s] = , s));
     while (!h.empty()) {
         pair p = h.top(); h.pop();
         if (dis[p.y] != p.x)continue;
         if (p.y == t)return dis[p.y];
         for (int i = hd[p.y]; ~i; i = nt[i])
             if (dis[to[i]] > dis[p.y] + vl[i])
                 h.push(pair(dis[to[i]] = dis[p.y] + vl[i], to[i]));
     }
     return dis[t];
 }

 inline int pos(int x, int y) {
     if (x ==  || y == n + )return s;
     if (y ==  || x == n + )return t;
     return (x - ) * n + y;
 }

 signed main(void) {
     n = nextInt();
     s = , t = n * n + ;
     for (int i = s; i <= t; ++i)hd[i] = -;
     for (int i = s; i <= t; ++i)dis[i] = inf;
     for (int i = ; i <= n; ++i)
         for (int j = ; j <= n; ++j)
             add(pos(i, j), pos(i + , j), nextInt());
     for (int i = ; i <= n; ++i)
         for (int j = ; j <= n; ++j)
             add(pos(i, j + ), pos(i, j), nextInt());
     for (int i = ; i <= n; ++i)
         for (int j = ; j <= n; ++j)
             add(pos(i + , j), pos(i, j), nextInt());
     for (int i = ; i <= n; ++i)
         for (int j = ; j <= n; ++j)
             add(pos(i, j), pos(i, j + ), nextInt());
     printf("%d\n", Dijkstra());
 }

@Author: YouSiki