Luogu P4643 【模板】动态dp

题目链接

Luogu P4643

题解

猫锟在WC2018讲的黑科技——动态DP，就是一个画风正常的DP问题再加上一个动态修改操作，就像这道题一样。（这道题也是PPT中的例题）

动态DP的一个套路是把DP转移方程写成矩阵乘法，然后用线段树（树上的话就是树剖）维护矩阵，这样就可以做到修改了。

注意这个“矩阵乘法”不一定是我们常见的那种乘法和加法组成的矩阵乘法。设\(A * B = C\)，常见的那种矩阵乘法是这样的：

\[C_{i, j} = \sum_{k = 1}^{n} A_{i, k} * B_{k, j}
\]

而这道题中的矩阵乘法是这样的：

\[C_{i, j} = \max_{k = 1}^{n} (A_{i, k} + B_{k, j})
\]

这就相当于常见矩阵乘法中的加法变成了max，乘法变成了加法。类似于乘法和加法的五种运算律，这两种变化也满足“加法交换律”、“加法结合律”、“max交换律”、“max结合律”和“加法分配律“。那么这种矩阵乘法显然也满足矩阵乘法结合律，就像正常的矩阵乘法一样，可以用线段树维护。

接下来我们来构造矩阵。首先研究DP方程。

就像“没有上司的舞会”一样，\(f_{i, 0}\)表示子树\(i\)中不选\(i\)的最大权独立集大小，\(f_{i, 1}\)表示子树\(i\)中选\(i\)的最大权独立集大小。

但这是动态DP，我们需要树链剖分。假设我们已经完成了树链剖分，剖出来的某条重链看起来就像这样，右边的是在树上深度较大的点：

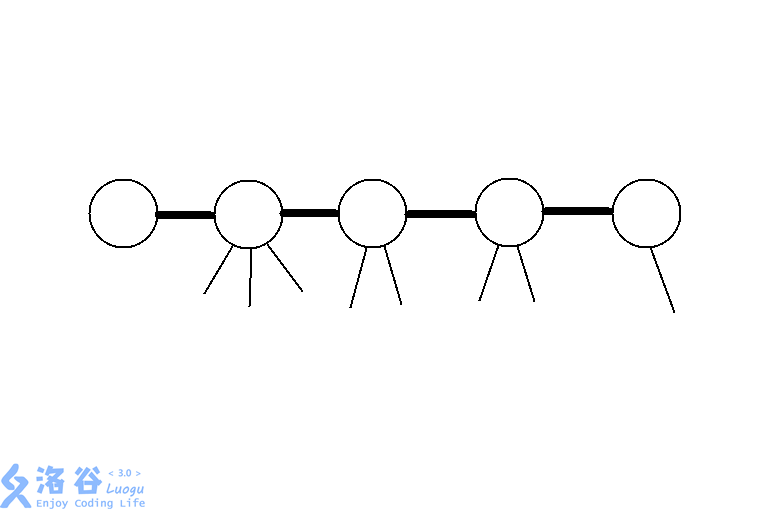
此时，比这条重链的top深度大且不在这条重链上的点的DP值都是已经求出来的（这可以做到）。我们把它们的贡献，都统一于它们在这条重链上对应的那个祖先上。

具体来说，设\(g_{i, 0}\)表示不选\(i\)时，\(i\)不在链上的子孙的最大权独立集大小，\(g_{i, 1}\)表示选\(i\)时，\(i\)不在链上的子孙再加上\(i\)自己的最大权独立集大小。

假如\(i\)右面的点是\(i + 1\), 那么可以得出：

\[f_{i, 0} = g_{i, 0} + \max(f_{i + 1, 0}, f_{i + 1, 1})
\]

\[f_{i, 1} = g_{i, 1} + f_{i + 1, 0}
\]

矩阵也就可以构造出来了：

\[\begin{bmatrix}g_{i, 0} & g_{i, 0} \\g_{i, 1} & 0\end{bmatrix} * \begin{bmatrix}f_{i + 1, 0} \\ f_{i + 1, 1}\end{bmatrix} = \begin{bmatrix}f_{i, 0} \\ f_{i, 1}\end{bmatrix}
\]

读者可以动笔验证一下。（注意我们在这里用的“新矩阵乘法”的规则：原来的乘变成加，加变成取max。）

那么基本思路就很清楚了：树剖，维护区间矩阵乘积。修改的时候，对于被修改节点到根节点路径上的每个重链（由下到上），先进行单点修改，然后求出这条重链的\(top\)在修改之后的\(f\)值，然后继续修改top所在重链。

每次答案就是节点\(1\)的\(f\)值。

代码

代码略丑，见谅……

#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
    char c;
    bool op = 0;
    while(c = getchar(), c < '0' || c > '9')
	if(c == '-') op = 1;
    x = c - '0';
    while(c = getchar(), c >= '0' && c <= '9')
	x = x * 10 + c - '0';
    if(op) x = -x;
}
template <class T>
void write(T x){
    if(x < 0) putchar('-'), x = -x;
    if(x >= 10) write(x / 10);
    putchar('0' + x % 10);
}

const int N = 100005;
int n, m, a[N];
int ecnt, adj[N], nxt[2*N], go[2*N];
int fa[N], son[N], sze[N], top[N], idx[N], pos[N], tot, ed[N];
ll f[N][2];

struct matrix {
    ll g[2][2];
    matrix(){
	memset(g, 0, sizeof(g));
    }
    matrix operator * (const matrix &b) const {
	matrix c;
	for(int i = 0; i < 2; i++)
	    for(int j = 0; j < 2; j++)
		for(int k = 0; k < 2; k++)
		    c.g[i][j] = max(c.g[i][j], g[i][k] + b.g[k][j]);
	return c;
    }
} val[N], data[4*N];

void add(int u, int v){
    go[++ecnt] = v;
    nxt[ecnt] = adj[u];
    adj[u] = ecnt;
}

void init(){
    static int que[N];
    que[1] = 1;
    for(int ql = 1, qr = 1; ql <= qr; ql++)
	for(int u = que[ql], e = adj[u], v; e; e = nxt[e])
	    if((v = go[e]) != fa[u])
		fa[v] = u, que[++qr] = v;
    for(int qr = n, u; qr; qr--){
	sze[u = que[qr]]++;
	sze[fa[u]] += sze[u];
	if(sze[u] > sze[son[fa[u]]])
	    son[fa[u]] = u;
    }
    for(int ql = 1, u; ql <= n; ql++)
	if(!top[u = que[ql]]){
	    for(int v = u; v; v = son[v])
		top[v] = u, idx[pos[v] = ++tot] = v;
	    ed[u] = tot;
	}
    for(int qr = n, u; qr; qr--){
	u = que[qr];
	f[u][1] = max(0, a[u]);
	for(int e = adj[u], v; e; e = nxt[e])
	    if(v = go[e], v != fa[u]){
		f[u][0] += max(f[v][0], f[v][1]);
		f[u][1] += f[v][0];
	    }
    }
}

void build(int k, int l, int r){
    if(l == r){
	ll g0 = 0, g1 = a[idx[l]];
	for(int u = idx[l], e = adj[u], v; e; e = nxt[e])
	    if((v = go[e]) != fa[u] && v != son[u])
		g0 += max(f[v][0], f[v][1]), g1 += f[v][0];
	data[k].g[0][0] = data[k].g[0][1] = g0;
	data[k].g[1][0] = g1;
	val[l] = data[k];
	return;
    }
    int mid = (l + r) >> 1;
    build(k << 1, l, mid);
    build(k << 1 | 1, mid + 1, r);
    data[k] = data[k << 1] * data[k << 1 | 1];
}
void change(int k, int l, int r, int p){
    if(l == r){
	data[k] = val[l];
	return;
    }
    int mid = (l + r) >> 1;
    if(p <= mid) change(k << 1, l, mid, p);
    else change(k << 1 | 1, mid + 1, r, p);
    data[k] = data[k << 1] * data[k << 1 | 1];
}
matrix query(int k, int l, int r, int ql, int qr){
    if(ql <= l && qr >= r) return data[k];
    int mid = (l + r) >> 1;
    if(qr <= mid) return query(k << 1, l, mid, ql, qr);
    if(ql > mid) return query(k << 1 | 1, mid + 1, r, ql, qr);
    return query(k << 1, l, mid, ql, qr) * query(k << 1 | 1, mid + 1, r, ql, qr);
}
matrix ask(int u){
    return query(1, 1, n, pos[top[u]], ed[top[u]]);
}
void path_change(int u, int x){
    val[pos[u]].g[1][0] += x - a[u];
    a[u] = x;
    matrix od, nw;
    while(u){
	od = ask(top[u]);
	change(1, 1, n, pos[u]);
	nw = ask(top[u]);
	u = fa[top[u]];
	val[pos[u]].g[0][0] += max(nw.g[0][0], nw.g[1][0]) - max(od.g[0][0], od.g[1][0]);
	val[pos[u]].g[0][1] = val[pos[u]].g[0][0];
	val[pos[u]].g[1][0] += nw.g[0][0] - od.g[0][0];
    }
}

int main(){

    read(n);
    read(m);
    for(int i = 1; i <= n; i++) read(a[i]);
    for(int i = 1, u, v; i < n; i++)
	read(u), read(v), add(u, v), add(v, u);
    init();
    build(1, 1, n);
    int u, x;
    matrix t;
    while(m--){
	read(u), read(x);
	path_change(u, x);
	t = ask(1);
	write(max(t.g[0][0], t.g[1][0])), enter;
    }

    return 0;
}