年少和 Smart の日常比赛 R3

在洛谷上参加了个比赛....写写题解 rank3....共5人...（捂脸

没有注明是官方代码的均是我比赛时本人提交的代码

T1  洗牌

题目描述

小明把 n (n 为偶数)张牌按编号顺序 1, 2, 3, …, n 排成一堆，然后开始洗牌。 一次洗牌的过程如下：

1. 对于一堆牌编号为 a1, a2, …, an，首先将牌分成均匀的两堆：a1, a2, …, am和 am+1, am+2, …, an (其中 m = n/2)

2. 然后按顺序交叉插入：a1, am+1, a2, am+2, …, am, an

洗牌过程总共重复了 k 次，请你编程帮助小明模拟洗牌的过程。

例如 n = 6， 初始时牌堆中牌的编号为 1, 2, 3, 4, 5, 6。首次洗牌时，会将牌分成 1, 2, 3 和 4, 5, 6 两堆， 交叉插入后的结果为 1, 4, 2, 5, 3, 6。再次洗牌，会将牌分成 1, 4, 2 和 5, 3, 6 两堆。 交叉插入后得到 1, 5, 4, 3, 2, 6。

输入输出格式

输入格式：

正整数 n (牌的数量), k (洗牌的次数), i (牌的位置)。 1 ≤ n, k ≤ 1,000， 1 ≤ i ≤ n，保证 n 是偶数。

输出格式：

n 张牌洗牌 k 次后， 牌堆中第 i 张牌的编号。

输入输出样例

输入样例#1：

6 2 5

输出样例#1：

2

输入样例#2：

400 300 200

输出样例#2：

368

说明

1 ≤ n, k ≤ 1,000， 1 ≤ i ≤ n，保证 n 是偶数。

题目大意

有1 2 3 4 5...n张牌，洗牌规则是，将牌分成两份，a1,a2,a3,am,和am+1,am+2,an，其中m=n/2

排成a1 am+1 a2 am+2.....求洗k次牌后第i张牌的编号

题解

模拟 开tmp数组存排完后的牌

#include<iostream>
#include<cstdio>
using namespace std;
int n,k,g,pos,mid,kk,j,t,st[],tmp[];
int main(){
    scanf("%d%d%d",&n,&kk,&pos);
    t=n;mid=n/+;n=n%;
//    if(n==0){printf("%d\n",pos);return 0;}
    for(int i=;i<=t;i++)st[i]=i;
    for(int i=;i<=kk;i++){
        k=;g=mid;j=;
        while(k<mid&&g<=t){
            tmp[++j]=st[k];
            tmp[++j]=st[g];
            k++;g++;
        }
        for(int a=;a<=t;a++)st[a]=tmp[a];
    }
    printf("%d\n",st[pos]);
    return ;
}

标程：比我的简洁多了....

#include<iostream>
#include<cstdio>
using namespace std;
int n,k,ii,a[],b[];
int main(){
    scanf("%d%d%d",&n,&k,&ii);
    for(int i=;i<=n;i++)a[i]=i;
    for(int i=;i<=k;i++){
        for(int j=;j<=n;j++)
        if(j%==)b[j]=a[(j+)/];
        else b[j]=a[n/+j/];
        for(int j=;j<=n;j++)a[j]=b[j];
    }
    printf("%d\n",a[ii]);
    return ;
}

T2  字符串替换

题目描述

小明最近迷上了字符串操作。 对每个字符串， 小明每次可以执行以下两种操作之一：

1. 把字符串中的某个字符改成任意一个其他字符，花费 1 的代价。

2. 交换字符串中的两个字符，花费 0 的代价。

小明发现，把一个字符串通过一系列的操作，可以转换成任何一个与之等长的字符串。 例如，把“hello” 变为“world” 的一种代价为 3 的操作序列如下：

1. hello → wello (替换 h 为 w，代价为 1)
2. wello → wolle (交换 e 和 o，代价为 0)
3. wolle → worle (替换 l 为 r，代价为 1)
4. worle → world (替换 e 为 d，代价为 1)

小明发现，无法用少于 3 次的代价将“hello”变为“world”。 显然，不同的转换方案花费的代价是不同的， 请编程帮助小明计算把一个字符串变为另一个字符串的最小代价。

本题中的字符串根据给定的初始数值 s 按以下规则生成：

for i = 1, 2, … n

s ← (s × 345) mod 19997

第一个字符串的第 i 个字符的 ASCII 码为(97 + (s mod 26))

for i = 1, 2, … n

s ← (s × 345) mod 19997

第二个字符串的第 i 个字符的 ASCII 码为(97 + (s mod 26))

输入输出格式

输入格式：

正整数 n (字符串长度), s (数据生成器的初始数值)。 1 ≤ n ≤ 1,000， 1 ≤ s ≤ 19,997。

输出格式：

将第一个字符串转换为第二个字符串的最少代价。

输入输出样例

输入样例#1：

4 35

输出样例#1：

2

输入样例#2：

100 31

输出样例#2：

29

说明

在样例 1 中，生成的字符串是“lzvv”和“ xylv”，将第一个字符串变为第二个的最小代价为 2。

题目大意

啊 这题我没做...

官方代码

#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
    int i,n,s,minn,ans=;
    int a[]={},b[]={};
    cin>>n>>s;
    for(i=;i<=n;++i){
        s=(s*)%;
        a['a'+s%]++;
    }
    for(i=;i<=n;++i){
        s=(s*)%;
        b['a'+s%]++;
    }
    for(i='a';i<='z';++i){
        minn=min(a[i],b[i]);
        ans+=a[i]-minn;
    }
    cout<<ans<<endl;
    return ;
}

T3 数列求和

题目描述

小明写出了一个数列， 第 i 项 ai的值为 i2。数列从第一项(i = 1)开始如下：1, 4, 9, 16, 25, …编程求出这个数列前 n 项的和。

输入输出格式

输入格式：

整数 n (1 ≤ n ≤ maxlonglong.)

输出格式：

一个整数： a1 + a2 + ··· + an的值。

输入输出样例

输入样例#1：

6

输出样例#1：

91

题目大意 

求1^2+2^2+...n^2的和

题解

我写（逃 了一大串高精度啊...不贴了...官方标程..

代码

#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
    int n,i,sum=;
    cin>>n;
    for(i=;i<=n;++i)
        sum+=i*i;
    cout<<sum<<endl;
    return ;
}

T4 堆木头

题目描述

有n根木头(2<=n<=10^20)，堆成k层(2≤k≤n)，要求下层木头数为上层木头数加1.

例如：n=6

堆法有

1种堆法。

n=9 堆法有

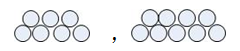
2种堆法。

n=4 不可能有符合条件的堆法。

输入输出格式

输入格式：

一个整数n。

输出格式：

一个整数，即堆法数，若不可能，则输出0.

输入输出样例

输入样例#1：

21

输出样例#1：

3

题解
唔...这题我不会...算了去看看叭...（5min后....
代码
60分做法暴力枚举第一层的层数

#include<iostream>
#include<cstdio>
using namespace std;
long long n,ans;
int main(){
    scanf("%lld",&n);
    for(int i=;i<=n-;i++){
        long long t=,k=i;
        while(){
            t+=k;k++;
            if(t==n){ans++;break;}
            if(t>n)break;
        }
    }
    printf("%lld\n",ans);
    return ;
}

100分做法 我把官方的pas翻译成了c++ 玄学

#include<iostream>
#include<cstdio>
using namespace std;
long long n,ans;
int main(){
    scanf("%lld",&n);n=n*;
    for(long long k=;k*k<n;k++){
        if(n%k==)if (((n/k)-k+)%==)ans++;
    }
    printf("%lld\n",ans);
    return ;
}

T5 Smart 的函数

题目描述

Smart定义p(n)表示n大于1的最小的约数，如P(5)=5，P(6)=2。

对于n，他又定义Smart函数F(n)为F(n)= p(2) + p(3) + …… + p(n)。

现在给你N的值，求N的Smart函数F(N)的值。

输入输出格式

输入格式：

输入一行，包含一个整数，即N。

输出格式：

输出一行，包含一个整数，表示所求的函数值。

输入输出样例

输入样例#1：

10

输出样例#1：

28

说明

60%的数据：N≤10^5；

100%的数据：2≤N≤5*10^7。

【样例说明】

P(2)=2，P(3)=3，P(4)=2，P(5)=5，P(6)=2，P(7)=7，P(8)=2，P(9)=3，P(10)=2.

F(10)=P(2)+P(3)+…+P(10)=2+3+2+5+2+7+2+3+2=28。

代码

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int f[],n;
int min_y(int x){
    int gg=x;
    for( gg=;gg<=x;gg++){
        if(x%gg==)break;
    }
    return gg;
}
int main(){
    scanf("%d",&n);f[]=;
//    for(int i=3;i<=8;i++)cout<<min_y(i)<<endl;
    for(int i=;i<=n;i++){
    f[i]=min_y(i)+f[i-];
    }
    printf("%d\n",f[n]);
    return ;
} 

T6 Smartの牛

题目描述

Smart 开办了一个农场。他在第一年的时候买了一只刚出生牛，这只牛在第四年的时候就能生一头小牛，以后每年这头牛就会生一头小牛。（出题人：不要问我为什么）

这些小牛成长到第四牛又会生小牛，以后每年同样会生一头牛，假设牛不死，如此反复。请问n年后，这个农场会有多少头牛？

输入输出格式

输入格式：

共一行。包含一个整数n。

输出格式：

共一行。包含一个整数，即n年后，Smart 的农场共有多少头牛。

输入输出样例

输入样例#1：

1

输出样例#1：

1

输入样例#2：

6

输出样例#2：

4

说明

对于 100% 的数据，n<=100000.

【样例说明】

第一头牛，它经过了第0年，第一年，第二年，第三年。生下一头小牛。牛总数为2.

（由于小牛要过四年才能生牛，所以不考虑）

由于第一头牛以后每年都生一头小牛，第四年生了一头，第五年也生了一头。

所以牛总数为 6.

题解 ：递推 ...f[i]为第i年的牛的数量，f[i]=f[i-3]+f[i-1],f[i-3]为经过了四年i-3年的那些牛生的小牛,再加上i-1的那些的牛

代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n;
int f[];
int main(){
    scanf("%d",&n);
    if(n<){printf("1\n");return ;}
    f[]=f[]=f[]=;
    for(int i=;i<=n;i++){
        f[i]=f[i-]+f[i-];
    }
    printf("%d",f[n]);
    return ;
}

T7 Smart的读书计划

题目描述

Smart 正在准备比赛，因为再过了几天他就要参加一场重要的比赛。于是他拿出了他的比赛秘籍，准备在两天之内研读完毕。但又有一个大问题，这本书太厚了！！Smart 急的抓耳挠腮。

正巧，Smart 的女友 Clever 来到了她家，Smart 心急如焚的询问该怎么读这本书。他说：“这本书一共有N页，分别是a1,a2···aN-1,aN，每一页上都会有一个比赛的'妙招'，a1,a2···aN-1,aN页上每页上的'妙招'，都有自己对应的编号，但是有许多'妙招'在书中重复说了很多遍，但是我现在时间不够，不能完整读完整本书，我想只读一些连续的页数，就能学完所有'妙招'，请你帮我想想办法呗！”Clever 想了想，把这个问题交给了会编程的你。你能帮 Smart 解忧吗？

输入输出格式

输入格式：

共 2 行。第一行为一个整数N，即书的页数。

第二行为 N 个非负整数，即每页对应 ‘妙招’的编号。

输出格式：

共一行。包含一个整数，即满足 Smart 条件的读书最少页数。

（Smart 的条件：我想只读一些连续的页数，就能学完所有'妙招'）

输入输出样例

输入样例#1：

4
1 3 3 1

输出样例#1：

2

说明

对于 100 % 的数据，N<=1000000.

保证每个 ‘妙招’ 的编号为非负整数，且在 int 范围内。

题目大意 求一段区间 使的这个区间包含总序列所有不重复的数且区间长度最小

题解 二分答案 二分区间长度看看能不能包含所有的数 能则缩小区间长度 否则变大区间长度

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<set>
using namespace std;
int n,bok[],tmp[];
int l,r,mid,siz,ans;
set<int>q;
int ok(int l){
    q.clear();
    for(int i=;i+l-<=n;i++){
        for(int j=i;j<=i+l-;j++){
          q.insert(tmp[j]);
        }
        if(q.size()==siz)return ;
        else q.clear() ;
    }
    return ;
}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++)scanf("%d",&bok[i]),tmp[i]=bok[i];
    sort(bok+,bok+n+);
    siz=unique(bok+,bok+n+)-bok-;
    l=,r=n;
    while(l<=r){
        mid=(l+r)>>;
        if(ok(mid))ans=mid,r=mid-;
        else l=mid+;
    }
    printf("%d",ans);
    return ;
}

T8 Smart 和 Clever 的纪念日

题目背景

年少来友情客串啦！！！

参演人员：Smart,Clever,年少。

题目描述

Smart 和 Clever 的一周年纪念日眼看着就要到来了。

Smart 是一个有选择恐惧症的人，他自己也不知道该送什么给自己的女友Clever，于是找来了他的deskmate：年少！

Smart 赶紧问年少该如何挑选礼物，不料，年少也不爱选择。正当两人愁眉苦脸时，年少突然说：“我虽然不能帮你选礼物，但我可以帮你计算！”Smart 又说：“正好，我妈最近几天要过生日了，我正好帮两人都买点礼物，你就帮我算算怎样分配才能使Clever 和我妈的礼物价值相差最小？”年少说：“没问题！”这时，Clever 飘了进来，对Smart 说：“别忘了明天是一周年哦~~”······

输入输出格式

输入格式：

共两行。第一行为一个整数，即 Smart 买的礼物个数 P。

第二行为 P 个整数，即每个礼物的价值。

输出格式：

共一行。包含一个整数，即所有礼物分成两组后的最小价值差。

输入输出样例

输入样例#1：

3
15 6 8

输出样例#1：

1

说明

对于 100 % 的数据，n<=35。

保证每个礼物的价值为非负整数，且<=15000.

题目大意

md做题还撒狗粮

有n个礼物 每个礼物有价值 求礼物分成两组后的最小价值差

题解

礼物排序后前缀和分组

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,v[],sum[],ans=;
int min_(int x,int y){return x<y?x:y;}
int abs_(int x){return x<?(-x):x;}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%d",&v[i]);
    }
    sort(v+,v+n+);
    for(int i=;i<=n;i++)sum[i]=sum[i-]+v[i];
    for(int i=;i<n;i++)ans=min_(ans,abs_(sum[i]-sum[n]+sum[i]));
    printf("%d",ans);
    return ;
} 

官方题解 DFS

#include <bits/stdc++.h>
#define max(a,b) a>b?a:b
int V,ans,n,w[],sum[];
void dfs(int i,int cnt)
{
    if(i == )
    {
        ans = max(ans,cnt);
        return ;
    }
    if(ans == V || cnt+sum[i] <= ans)
        return ;
    if(cnt+w[i] <= V)
        dfs(i-,cnt+w[i]);
    dfs(i-,cnt);
}
int main()
{
    scanf("%d",&n);
    ans = ;
    for(int i=;i<=n;i++)
    {
        scanf("%d",&w[i]);
        sum[i] = sum[i-] + w[i];
    }
    V = sum[n]/;
    dfs(n,);
    printf("%d\n",sum[n]-*ans);
    return ;
}