bzoj 5015 [Snoi2017]礼物

题面

https://www.lydsy.com/JudgeOnline/problem.php?id=5015

题解

首先把k=1,k=2,k=3的手推一遍

然后发现一些规律 就是数列可以表示成$a_i=2a_{i-1}+f(i)$的形式

然后f(i)算一算之后我们得到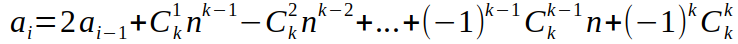

然后我们试图求这个东西的通项公式

我们要把它变成$a_i+f(i)=2(a_{i-1}+f(i-1))$的形式就好了

那么我们设

一共k个变量 对于每一个$n^i$我们根据他的系数可以列一个方程 一共k个方程

所以高斯消元把它解出来就结束了

Code

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;

 ll read(){
     ll x=,f=;char c=getchar();
     while(c<'' || c>''){if(c=='-')f=-;c=getchar();}
     while(c>='' && c<=''){x=x*+c-'';c=getchar();}
     return x*f;
 }

 const ll mod=1000000007ll;
 ll n;
 int k;
 ll mat[][];

 ll calc(ll a,ll b){
     ll ret=;
     for(int i=;i<=b;i++)
         ret=ret*(a-i+)/i;
     return ret%mod;
 }

 ll ksm(ll a,ll b){
     if(b==) return ;
     ll nw=;
     if(b==) return a%mod;
     if(b&) nw=a;
     ll ret=ksm(a,b/);
     return ret*(nw%mod)%mod*ret%mod;
 }

 inline ll pd(ll x){
     if(x&) return -;
     return ;
 }
 ll ans[];

 int main(){
     #ifdef LZT
     //freopen("in","r",stdin);
     #endif
     n=read(),k=read();
     for(int i=;i<=k;i++){
         mat[i][]=calc(k,i)*pd(i+);
         mat[i][i]--;
         int st=i-;
         for(int j=;j<=i;j++)
             mat[i][j]+=(*calc(k-j,st)*pd(st--));
     }
     for(int i=;i<=k;i++){
         ll nw=;
         for(int j=;j<i;j++) nw=nw+mat[i][j]*ans[j];
         ans[i]=(mat[i][]-nw)/mat[i][i];
     }
     for(int i=;i<=k;i++)
         ans[i]=ans[i]%mod;
     ll res=ans[k]*ksm(,n)%mod;
     for(int i=;i<=k;i++){
         ll nw=ans[i]*ksm(n,k-i)%mod;
         res=(res-nw+mod)%mod;
     }
     printf("%lld\n",res);

     return ;
 }

Review

这样做的动机?

就是先把k=2,k=3的情况推了一下 然后发现很相似 f(i)的次数与k相关而k很小 只有10

然后就试图用程序表达手推的过程 发现消元就可以了 然后就做了出来