[ NOIP 2002 ] TG

\(\\\)

\(\#A\) 均分纸牌

---

有\(N\)堆纸牌，每堆有若干张，但纸牌总数必为\(N\)的倍数。可以在任一堆上取若干张纸牌，然后移动给其左右任意一侧的纸牌堆，求将所有的牌堆牌数都变为平均值最少移动次数。

• \(N\in [0,100]\)

• 把所有数减掉平均数，自左往右扫描，只要当前数不为\(0\)，就将这个数加给右侧的数，累加计数器。
• 如果加上了一个负数，代表从右侧的堆移动给了左侧，正数则相反。

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 110
#define R register
#define gc getchar
using namespace std;

inline int rd(){
  int x=0; char c=gc();
  while(!isdigit(c)) c=gc();
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return x;
}

int ave,ans,a[N];

int main(){
  int n=rd();
  for(R int i=1;i<=n;++i) ave+=(a[i]=rd());
  ave/=n;
  for(R int i=1;i<=n;++i) a[i]-=ave;
  for(R int i=1;i<=n;++i){
    ans+=(abs(a[i])>0); a[i+1]+=a[i];
  }
  printf("%d\n",ans);
  return 0;
}

\(\\\)

\(\# B\) 字串变换

---

给定两个字符串\(A,B\)，以及\(N\)个映射\(U_i\rightarrow V_i\)，问是否能在十次操作之内通过子串映射的方式将\(A\)改为\(B\)。

• \(len_A,len_B\in [1,20]\)，\(N\in [1,20]\)

• 为了找到最少次数可以考虑\(BFS\)，每次找到一个位置，替换，次数加一加入队列，第一个找到的数为答案。
• 为了避免重复搜索同一个串，可以使用\(map\)判断，字符串处理上要注意string自带的函数真**强。

#include<map>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<string>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define R register
#define N 30
using namespace std;

int tot=1,res;
string a,b,org[N],trs[N];
map<string,int> mp;
queue<pair<string,int> > q;

inline string check(string s,int p,int k){
  string res="";
  if(p+org[k].size()-1>s.size()) return res;
  for(R int i=0;i<org[k].size();++i)
    if(s[p+i]!=org[k][i])return res;
  s.replace(p,org[k].size(),trs[k]);
  return s;
}

int main(){
  cin>>a>>b;
  while(cin>>org[tot]>>trs[tot]) ++tot;
  q.push(make_pair(a,0));
  while(!q.empty()){
    int u=q.front().second;
    string su=q.front().first; q.pop();
    if(!mp[su]) mp[su]=u;
    else continue;
    if(u>10) break;
    if(su==b){res=u;break;}
    for(R int i=0;i<su.size();++i)
      for(R int j=1;j<=tot;++j){
        string sv=check(su,i,j);
        if(sv=="") continue;
        q.push(make_pair(sv,u+1));
    }
  }
  if(res) printf("%d\n",res);
  else puts("NO ANSWER!");
  return 0;
}

\(\\\)

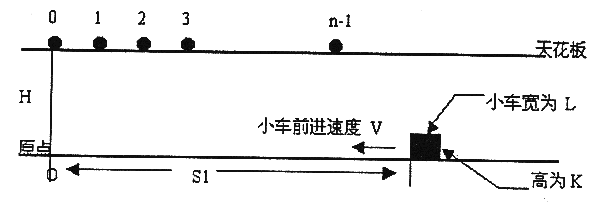
\(\#C\) 自由落体

---

在高为\(H\)的天花板上有\(n\)个小球，体积不计，位置分别为\(0,1,2,…,n-1\)。

在地面上有一个小车（长为\(L\)，高为\(K\)，距原点距离为\(S_1\)）。

已知小球下落距离计算公式为d\(=0.5 \times g \times (t^2)\)，其中\(g=10\)，\(t\)为下落时间。地面上的小车以速度\(V\)前进。

小车与所有小球同时开始运动，当小球距小车的距离\(\le 0.0001\)时，即认为小球被小车接受（小球落到地面后不能被接受），计算小车能接受到多少个小球。

• \(1\le H,S_1,V,L,K,n\le 100000\)

• 解公式，小车在球落地前最远能到达的位置为\(S_2=S_1-V\times \sqrt\frac{2H}{g}\)
• 最早能接到球且最靠后的位置为\(S_3=S_1-V\times \sqrt\frac{2(H-K)}{g}+L\)
• 判断区间\([S2,S3]\bigcap[1,n]\)内的整点个数即可，注意精度的限制。

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define R register
using namespace std;
typedef double db;

double eps=1e-4;

int main(){
  db h,s,v,l,k,n;
  scanf("%lf%lf%lf%lf%lf%lf",&h,&s,&v,&l,&k,&n);
  double t1=sqrt(h/5),t2=sqrt((h-k)/5);
  double s1=s-t1*v,s2=s-t2*v+l;
  int resl=(int)ceil(max(s1-eps,(double)0)),resr=floor(min(n-1,s2+eps));
  printf("%d\n",max(0,resr-resl+1));
  return 0;
}

\(\\\)

\(\#D\) 矩形覆盖

---

给出\(N\)个第一象限的整点，求至多用\(K\)个矩形将其全部覆盖，矩形面积和最小是多少。

矩形可以是点或线，此时面积为\(0\)，但所选矩形不可出现面积相交、边相交、顶点相同的情况。

• \(N\in [1,50]\)，\(K\in [1,4]\)

\(DFS:\)

• 直接钦定每一个点属于哪一个矩形即可，剪枝如下：
  • 每一层判断当前矩形中是否出现不合法情况
  • 当前面积超过已经搜到过的答案
• 判断有交可以通过分别判断两个维度各自是否有交再去与得到。

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 60
#define R register
#define gc getchar
#define inf 2000000000
using namespace std;

int n,k,res=inf,l[5],r[5],u[5],d[5];
struct point{int x,y;}p[N];

inline int rd(){
  int x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

inline bool check(){
  for(R int i=0;i<k;++i)
    for(R int j=0;j<i;++j){
      bool y=((u[i]>=d[j]&&u[i]<=u[j])||(u[j]>=d[i]&&u[j]<=u[i]));
      bool x=((r[i]>=l[j]&&r[i]<=r[j])||(l[i]>=l[j]&&l[i]<=r[j]));
      if(x&&y) return 1;
    }
  return 0;
}

void dfs(int x,int sum){
  if(check()||sum>=res) return;
  if(x>n){res=sum;return;}
  for(R int i=0;i<k;++i){
    int lsts=(l[i]==inf?0:(r[i]-l[i])*(u[i]-d[i]));
    int lstl=l[i],lstr=r[i],lstu=u[i],lstd=d[i];
    l[i]=min(l[i],p[x].x); r[i]=max(r[i],p[x].x);
    d[i]=min(d[i],p[x].y); u[i]=max(u[i],p[x].y);
    dfs(x+1,sum-lsts+(r[i]-l[i])*(u[i]-d[i]));
    l[i]=lstl; r[i]=lstr; u[i]=lstu; d[i]=lstd;
  }
}

int main(){
  n=rd(); k=rd();
  for(R int i=0;i<k;++i){l[i]=d[i]=inf;r[i]=u[i]=-inf;}
  for(R int i=1;i<=n;++i){p[i].x=rd();p[i].y=rd();}
  dfs(1,0);
  printf("%d\n",res);
  return 0;
}

\(DP:\)

• 本方法已被证明不是完全正确的，但可以通过当年的数据，由于思想可以借鉴所以还是写一写。
• 首先，按照横坐标为第一关键字，纵坐标为第二关键字排序，设\(f[i][j][k]\)为从第\(i\)个点覆盖到第\(j\)个点用\(k\)个矩形所需的最小面积和。
• 类区间\(DP\)的思想，枚举断点和两侧的矩形个数，暴力更新。
• 注意到这样做得到的矩形都是并排的，所以我们需要将坐标系转\(\frac{\pi}{2}\)再做一遍。
• 当\(4\)个矩形时即可构造数据卡掉这个情况，只需要让横纵向答案都不是并排的即可。

#include<cmath>
#include<cctype>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 60
#define R register
#define gc getchar
#define inf 2000000000
using namespace std;

int n,m,f[N][N][5];
struct point{int x,y;}p[N];

inline int rd(){
  int x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

inline bool cmp(point x,point y){
  return (x.x==y.x)?x.y<y.y:x.x<y.x;
}

int main(){
  n=rd(); m=rd();
  for(R int i=0;i<n;++i){p[i].x=rd();p[i].y=rd();}
  sort(p,p+n,cmp);
  memset(f,0x3f,sizeof(f));
  for(R int i=0;i<n;++i)
    for(R int j=i+1;j<n;++j){
      int l=inf,r=-inf;
      for(R int k=i;k<=j;++k){l=min(l,p[k].y);r=max(r,p[k].y);}
      f[i][j][1]=(r-l)*(p[j].x-p[i].x);
    }
  if(m==1){printf("%d\n",f[0][n-1][1]);return 0;}
  for(R int i=n-1;i>=0;--i)
    for(R int j=i+1;j<n;++j)
      for(R int k=2;k<=m;++k)
        for(R int p=i+1;p<j;++p)
          for(R int t=1;t<k;++t)
            if(f[i][j][k])f[i][j][k]=min(f[i][j][k],f[i][p][t]+f[p+1][j][k-t]);
            else f[i][j][k]=f[i][p][t]+f[p+1][j][k-t];
  int res=f[0][n-1][m];
  for(R int i=0;i<n;++i) swap(p[i].x,p[i].y);
  sort(p,p+n,cmp);
  memset(f,0x3f,sizeof(f));
  for(R int i=0;i<n;++i)
    for(R int j=i+1;j<n;++j){
      int l=inf,r=-inf;
      for(R int k=i;k<=j;++k){l=min(l,p[k].y);r=max(r,p[k].y);}
      f[i][j][1]=(r-l)*(p[j].x-p[i].x);
    }
  if(m==1){printf("%d\n",f[0][n-1][1]);return 0;}
  for(R int i=n-1;i>=0;--i)
    for(R int j=i+1;j<n;++j)
      for(R int k=2;k<=m;++k)
        for(R int p=i+1;p<j;++p)
          for(R int t=1;t<k;++t)
            if(f[i][j][k])f[i][j][k]=min(f[i][j][k],f[i][p][t]+f[p+1][j][k-t]);
            else f[i][j][k]=f[i][p][t]+f[p+1][j][k-t];
  printf("%d\n",min(res,f[0][n-1][m]));
  return 0;
}