NOI2015 荷马史诗【k-哈夫曼树】

题目

追逐影子的人，自己就是影子 ——荷马

Allison 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了，Allison 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有n种不同的单词，从1到n进行编号。其中第i种单词出现的总次数为wi。Allison 想要用k进制串si来替换第i种单词，使得其满足如下要求：

对于任意的 1 ≤ i, j ≤ n ， i ≠ j ，都有：si不是sj的前缀。

现在 Allison 想要知道，如何选择si，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的si的最短长度是多少？

一个字符串被称为k进制字符串，当且仅当它的每个字符是 0 到 k − 1 之间（包括 0 和 k − 1 ）的整数。

字符串 str1 被称为字符串 str2 的前缀，当且仅当：存在 1 ≤ t ≤ m ，使得str1 = str2[1..t]。其中，m是字符串str2的长度，str2[1..t] 表示str2的前t个字符组成的字符串。

输入格式

输入的第 1 行包含 2 个正整数 n, k ，中间用单个空格隔开，表示共有 n种单词，需要使用k进制字符串进行替换。

接下来n行，第 i + 1 行包含 1 个非负整数wi ，表示第 i 种单词的出现次数。

输出格式

输出包括 2 行。

第 1 行输出 1 个整数，为《荷马史诗》经过重新编码以后的最短长度。

第 2 行输出 1 个整数，为保证最短总长度的情况下，最长字符串 si 的最短长度。

输入样例

4 2

1

1

2

2

输出样例

12

2

提示

【样例说明 1】

用 X(k) 表示 X 是以 k 进制表示的字符串。

一种最优方案：令 00(2) 替换第 1 种单词， 01(2) 替换第 2 种单词， 10(2) 替换第 3 种单词，11(2) 替换第 4 种单词。在这种方案下，编码以后的最短长度为：

1 × 2 + 1 × 2 + 2 × 2 + 2 × 2 = 12

最长字符串si的长度为 2 。

一种非最优方案：令 000(2) 替换第 1 种单词，001(2) 替换第 2 种单词，01(2)替换第 3 种单词，1(2) 替换第 4 种单词。在这种方案下，编码以后的最短长度为：

1 × 3 + 1 × 3 + 2 × 2 + 2 × 1 = 12

最长字符串 si 的长度为 3 。与最优方案相比，文章的长度相同，但是最长字符串的长度更长一些。

【样例说明 2】

一种最优方案：令 000(3) 替换第 1 种单词，001(3) 替换第 2 种单词，01(3) 替换第 3 种单词， 02(3) 替换第 4 种单词， 1(3) 替换第 5 种单词， 2(3) 替换第 6 种单词。

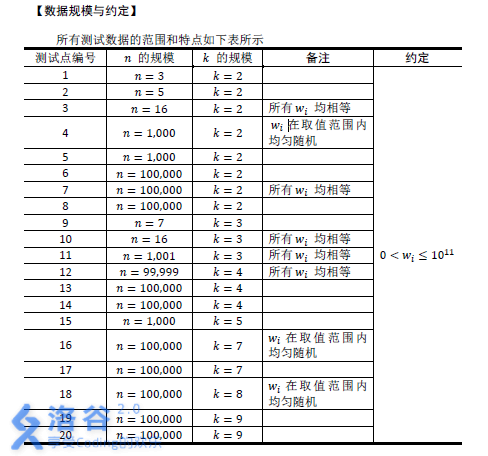
【提示】

选手请注意使用 64 位整数进行输入输出、存储和计算。

【时限1s，内存512M】

题解

当k=2时，就等同于合并果子，每次合并权值最小的两堆

将每次合并的一堆作为父亲，被合并的两堆作为儿子，就会形成一棵树，叫做哈夫曼树

哈夫曼树中所有点到根的距离乘以权值之和最小

通常用于编码，给各种需要的信息附上不同的01串，使得文章最短，当然是出现次数越多的信息赋的01串越短

如果是K进制，就要用上K哈夫曼树，实际上就是每次合并K堆

合并到最后不足K堆怎么办？

每一次合并会减少K - 1堆，所以只要n - 1是k - 1的倍数就可以了，用0补齐

题目还要求最大深度最小，权值相同时深度小的优先即可

#include<iostream>

#include<cstdio>

#include<cmath>

#include<queue>

#include<cstring>

#include<algorithm>

#define LL long long int

#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)

#define REP(i,n) for (int i = 1; i <= (n); i++)

#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");

using namespace std;

const int maxn = 100005,maxm = 100005,INF = 1000000000;

inline LL read(){

	LL out = 0,flag = 1; char c = getchar();

	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}

	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}

	return out * flag;

}

struct node{LL w,d;};

inline bool operator <(const node& a,const node& b){

	return a.w == b.w ? a.d > b.d : a.w > b.w;

}

priority_queue<node> q;

int n,k;

int main(){

	n = read(); k = read();

	REP(i,n) q.push((node){read(),0});

	while ((n - 1) % (k - 1) != 0) q.push((node){0,0}),n++;

	LL ans = 0,sum,d;

	while (n > 1){

		sum = 0; d = 0;

		for (int i = 1; i <= k; i++) sum += q.top().w,d = max(d,q.top().d),q.pop();

		ans += sum;

		q.push((node){sum,d + 1});

		n -= k - 1;

	}

	printf("%lld\n%lld\n",ans,q.top().d);

	return 0;

}