【Luogu】P1231教辅的组成（拆点+Dinic+当前弧优化）

　　题目链接

　　妈耶

　　我的图建反了两次　　　　准确的说是有两个地方建反了，然后反上加反改了一个小时……

　　知道为什么要拆点吗？

　　

　　假设这是你的图   左边到右边依次是超级源点    练习册     书     答案     超级汇点

　　请问这张图的最大流是多少？

　　如果把中间拆成这样：

　　

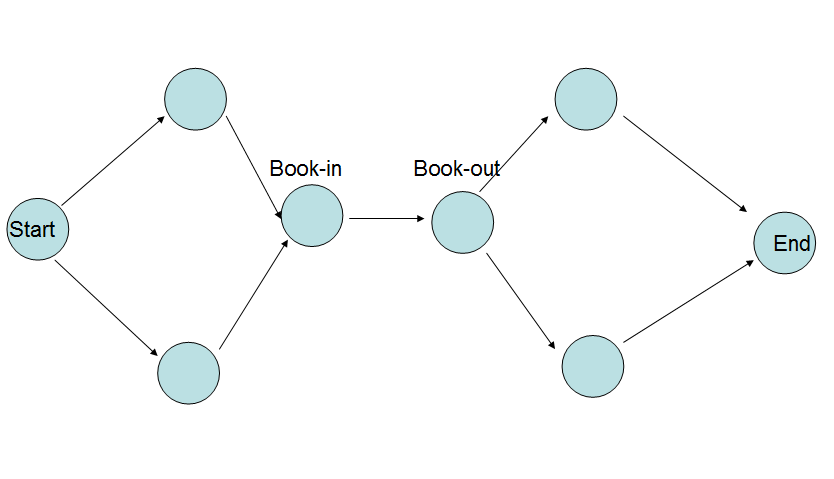
　　Book-in是跟练习册匹配的书的入端，Book-out是跟答案匹配的书的出端。相当于每本书都是一条隧道，有入口有出口，每本书的入口和对应的出口连边。

　　请问现在这张图的最大流是多少？

　　所以你看。

　　代码放上：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cctype>

inline long long read(){
    long long num=,f=;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')    f=-;
        ch=getchar();
    }
    while(isdigit(ch)){
        num=num*+ch-'';
        ch=getchar();
    }
    return num*f;
}

struct Edge{
    int next,to,val;
}edge[];
int head[],num=-;
inline void add(int from,int to,int val){
    edge[++num]=(Edge){    head[from],to,val};
    head[from]=num;
}

bool vis[];
int dfn[];
int list[];
int f[],h,t=;
int n,m,Start,End;

bool bfs(){
    memset(vis,,sizeof(vis));
    f[]=Start;vis[Start]=;dfn[Start]=;h=;t=;
    while(h++<t){
        int from=f[h];
        for(int i=head[from];i!=-;i=edge[i].next){
            int to=edge[i].to;
            if(vis[to]||(!edge[i].val))    continue;
            dfn[to]=dfn[from]+;
            vis[to]=;
            f[++t]=to;
        }
    }
    return vis[End];
}

int dfs(int x,int val){
    if(x==End||val==)    return val;
    int flow=;
    vis[x]=;
    for(int &i=list[x];i!=-;i=edge[i].next){
        int to=edge[i].to;
        if(dfn[to]==dfn[x]+&&!vis[to]&&edge[i].val>){
            int now=dfs(to,std::min(edge[i].val,val));
            if(now>){
                edge[i].val-=now;
                edge[i^].val+=now;
                flow+=now;val-=now;
                if(val<=)    break;
            }
        }
    }
    if(flow!=val)    dfn[x]=-;
    return flow;
}

int ans;

int main(){
    memset(head,-,sizeof(head));
    int n1=read(),n2=read(),n3=read();
    int n=n1*+n2;int N=n+n3;End=N+;
    int m1=read();
    for(int i=;i<=m1;++i){
        int book=read(),note=read();
        add(note+n1*,book,);
        add(book,note+n1*,);
    }
    int m2=read();
    for(int i=;i<=m2;++i){
        int book=read(),ansnote=read();
        add(book+n1,ansnote+n,);
        add(ansnote+n,book+n1,);
    }
    for(int i=;i<=n1;++i){
        add(i,i+n1,);
        add(i+n1,i,);
    }
    for(int i=;i<=n2;++i){
        add(Start,i+n1*,);
        add(i+n1*,Start,);
    }
    for(int i=;i<=n3;++i){
        add(i+n,End,);
        add(End,i+n,);
    }
    while(bfs()){
        memset(vis,,sizeof(vis));
        for(int i=;i<=End;++i)    list[i]=head[i];
        int now=dfs(Start,0x7fffffff);
        if(!now)    break;
        ans+=now;
    }
    printf("%d",ans);
    return ;
}

　　话说当前弧优化真好用