NOIP前的刷题记录

因为这几天要加油，懒得每篇都来写题解了，就这里记录一下加上一句话题解好了

P4071 [SDOI2016]排列计数   组合数+错排

loj 6217 扑克牌 暴力背包

P2511 [HAOI2008]木棍分割

第一问二分，第二问记$dp[i][j]$为前$i$根砍$j$刀的方案，那么它可以由所有$sum[i]-sum[k]<=ans1$的$k$转移而来，用滚动数组优化空间，用队列的形式优化转移

P1410 子序列

贪心能过（数据水）。dp的话，考虑$f[i][j]$表示前面$i$个数的最长上升子序列长度为$j$，剩下的$i-j$个数也构成上升序列时的末尾最小值。如果$a[i]<a[i+1]$，那么$f[i][j]$可以转移到$f[i+1][j+1]$，如果$f[i][j]<a[i+1]$，那么$a[i]$能转移到$f[i+1][i+1-j]$

CF183D T-shirt

题解简单来说就是随着每一种颜色取得越来越多对答案的贡献越来越少，所以这是一个上凸函数。然后考虑枚举每一种颜色每一次对答案的贡献，每一次选取一种颜色+1即可

P3298 [SDOI2013]泉

先暴力枚举哪几个位置相等，然后用哈希判是否相等，最后用容斥，设$ans_k$表示有大于等于$k$个相等时的答案，那么答案就是$ans_k-ans_{k+1}+ans_{k+2}...$

upd：前面的容斥系数好像还得配上一个组合数

吐槽一句：我找的这题单是NOIP任务还是ZJOI任务啊喂！

P4035 [JSOI2008]球形空间产生器

先把几个方程列出来，然后相邻方程之间减一减，能把它化为n元一次方程的形式，高斯消元带进去求解

P2783 有机化学之神偶尔会做作弊

无向图用tarjan缩点然后就是一个求树上路径长的问题了，树剖lca搞定

P3705 [SDOI2017]新生舞会

先二分答案$C$然后转化成所有的$a_i-C*b_i=0$，然后建二分图，源向男的连边，女的向汇连边，都是容1费0，然后男女连边容1费$a_i-C*b_j$，跑一个最大费用最大流，如果费用大于0说明该方案可行

P3174 [HAOI2009]毛毛虫

设链上每点入度为$a_i$，链上的总点数是$\sum a_i$，设$n$为链长，那么发现链上的$n-1$条边被多算了一次，也就是说有$n-2$个点被多算了一次，答案实际是$\sum a_i-n+2=\sum (a_i-1)+2$，设每个点点权为$a_i-1$，然后两次dfs跑最长路即可

P3244 [HNOI2015]落忆枫音

题解

P3243 [HNOI2015]菜肴制作

首先正解不是字典序最小的拓扑排序，随便构造几组都能发现错。于是我们考虑反向图字典序最大的拓扑排序即可

P4139 上帝与集合的正确用法

考虑扩展欧拉定理，有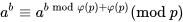，递归计算直到模数为1

P1344 [USACO4.4]追查坏牛奶Pollutant Control

首先第一问就是最小割，求最小边数的话，把每条边的流量变为$a=a*x+1$，其中$x$为一个大于边数的常数，那么在这个图上跑出来的最小割为$ans$，$ans/mod$为第一问的答案，$ans\%mod$为第二问的答案

P2827 蚯蚓

设a1为被切出的px，a2为x-px，然后发现a1和a2都具有单调性。于是对原数组排序，然后开三个队列，每一次都三个队列队首取出最大元素

P3615 如厕计划

正解向kkk说的那样跑一个贪心就好了，就是找最小后缀和的时候，注意应该是先找本段的最小后缀，然后根据本段总和是否小于零判断本段是否要重复$k_i-1$次

bzoj3744: Gty的妹子序列

分块+树状数组，然而这题太尼玛卡常了……

bzoj3622: 已经没有什么好害怕的了

并不是很想救麻美。dp+容斥。首先题目的意思可以转化成刚好选出$m=(n+k)/2$组使得药片大于糖果。先把两个数组都排序一遍，对第一个数组算出第二个数组中比它小的数的个数$nxt[i]$，设$f[i][j]$表示前$i$组中至少有$j$组满足第一个大于第二个（剩下的随意组合），那么方程就是$f[i][j]=f[i-1][j]+f[i-1][j-1]*max(0,nxt[i]-j+1)$。因为剩下的$n-j$个数可以随意匹配所以共有$(n-i)!$种方案，设$dp[j]=f[n][j]*(n-i)!$表示至少有$j$组的答案，考虑怎么求出刚好$j$组的答案，显然这是一个容斥。倒叙计算，设$i>j$，那么$dp[i]$的答案在$dp[j]$中被计算了$c[i][j]$次所以要减掉。然后倒序计算并不断减去所有$i>j$的答案即可

P1860 新魔法药水

设$ans[i][j]$表示第$i$个药水用$j$次魔法的最小花费，然后对于每一个魔法，设$ant[i][j]$表示该魔法所需原材料的前$i$个备齐且用了$j$次魔法的最小花费，因为魔法合成关系可能成环，所以魔法次数每增加一次要重新dp。然后设$dp[i][j]$表示$i$元钱$j$次魔法最大收益，转移即可

P3205 [HNOI2010]合唱队

区间dp，设$dp[i][j][k]$表示区间$[i,j]$最后一个人为左边插入还是右边插入的方案，枚举情况转移即可。注意为了防止单独一个数的区间被加两遍，可以设单独一个数只有是从左边被插入才是1否则是0

bzoj4361: isn

记录$f[i][j]$表示以$i$结尾的长度为$j$的非降序列的个数，用树状数组可以优化到$O(n^2logn)$。记$g[i]$为长度为$i$的非降序列个数，考虑$ans[i]=g[i]*(n-i)!$，然而有可能删到一半这个数组已经有序了。考虑一个非法的删除序列，肯定是由$i+1$个数删除得来的，所以枚举删的是哪一个数，减去$g[i+1]*(n-i-1)!*(i+1)$

P3478 [POI2008]STA-Station

树形dp，记录$dw[i]$表示点$i$下面的点到$i$的距离之和，$up[i]$表示除了下面的点之外的其他点到他的距离之和，两边dfs之后看一下哪个点最优即可

P3830 [SHOI2012]随机树

题解第二问还没搞懂为什么要除以$x-1$

bzoj4300: 绝世好题

dp，记$f[i]$为当前第$i$位不为零时的最大长度，转移就是$dp[i]=max(f[j]+1)(a[i]\&(1<<j)!=0)$，然后做完再用$dp[i]$去更新$f$即可

P2523 [HAOI2011]Problem c

首先记录$sum[i]$表示确定的位置大于等于$i$的人的个数，如果$sum[i]>n-i+1$显然无解。考虑dp，设$f[i][j]$表示剩余的人中编号大于等于$i$的人已经有$j$个确定了，那么$f[i][j]=\sum f[i+1][j-k]*C_{j}^k$，就是枚举有多少人没有编号把他们全都赋值为$i$，然后因为这些人选法不同所以再乘上一个$C_{j}^k$，然后从后往前转移即可

P2159 [SHOI2009]舞会

这题和之前那道bzoj3622无头麻美异闻录是一样的，然而恶心的是这题要打高精……高精减的板子写错调的我快哭出来了……

P2215 [HAOI2007]上升序列

倒叙求一个最长下降子序列，然后每一次一遍搞过去就好了

P2014 选课

树形dp，注意转移的顺序

jzoj5904. 【NOIP2018模拟10.15】刺客信条（AC）

二分+并查集，如果两个点距离小于mid就相连，最后判断上下/左右/上右/下左边界是否被连到一起。然而我忘了两个点之间的距离是半径的两倍了orz

jzoj5905. 【NOIP2018模拟10.15】黑暗之魂(darksoul)

0.5倍经验题……有重边和自环的部分就是个裸的求直径，不过注意重边得选权值小的那条。先把环给找出来，然后把环上每个点当做树的根求一遍最大深度（每个点不能dfs到环上其他点），就转化为环上选两个点使他们距离加两个点的权值（即最大深度）最大，先把数组倍长一遍破环成链，然后用单调队列维护即可（就是保证单调队列队首到该点的距离小于等于环长的一半，且$dis(i,q[t])+deepest[q[t]]\geq deepest[i]$）

jzoj5906. 【NOIP2018模拟10.15】传送门 （portal）

被样例误导了……首先没有传送门走的路径就是子树边权的两倍。然后有一个性质，如果从一个子树传了回来再走进这个子树不会更优。证明如下：我们走进去肯定是因为我们传送回来的地方和还没走的地方在某个地方分叉了，那么我们可以在那个分叉点设传送门，再暴力走回来，这样分叉到当前点走两遍，分叉以下都走一遍。于是设$g[i]$表示不设传送门的路径（即边权和的两倍），$f[i]$表示设传送门。假设儿子为$v$，可以暴力走$v$最后从最深的叶子传送回来，也可以在$v$开传送门然后暴力走这条边两次，那么转移就是$f[i]+=min(g[v]+edge(i,v)-deepest[v],2*edge(i,v)+f[v])$

P2619 [国家集训队2]Tree I

应该算是wqs二分的思想？简单来说就是二分一个权值mid令所有白边都加上，然后跑一遍最小生成树看看选的白边数量，少于need就调小mid否则调大，最后计算答案的时候减去mid的贡献即可

P4383 [八省联考2018]林克卡特树lct

题解本来以为已经看懂wqs二分了结果这尼玛是什么东西……

CF248E Piglet's Birthday

题解

jzoj5922. 【NOIP2018模拟10.23】sequence ，jzoj5923. 【NOIP2018模拟10.23】Bomb ，jzoj5924. 【NOIP2018模拟10.23】Queue

题解

jzoj5919. 【NOIP2018模拟10.22】逛公园

因为这是一棵仙……仙人掌，我们先跑出每一个环上最大和最小的标号，那么选数的区间绝对不能跨过这两个点。记$f[i]$表示选了$i$点右边最大能选哪个点，发现这东西是单调不降的，于是跑完环后从后往前dp一遍。然后对于每个询问$[l,r]$，我们暴力找出点$x$满足$f[x-1]<r$且$f[x]\geq r$，那么区间$[l,x-1]$的答案都是自己的$f$，剩下的就构成了一个等差数列。于是维护一下$f[i]-i+1$的前缀和以及$i$的前缀和就可以了

CF650D Zip-line

离线+树状数组。修改后分两种情况，一是$b_i$在LIS中，一种是不在LIS中。如果不在LIS中，把询问离线，对于每一个$b$判断左边能转移到它的最长的是多少，右边同理。正着跑一遍反着跑一遍，设原来的LIS长度为$k$，那么答案就是$max(k,ansl[i]+ansr[i]+1)$。如果在LIS中，那么看看去掉$a_i$会不会使LIS长度改变，就是说这个点同时出现在所有LIS中。有一个推论，如果一个点同时出现在所有LIS中，那么它在这些LIS中出现在同一个位置。于是正着跑一遍，对于每一个在LIS中的点，$L[i]$（正着跑时到它的LIS）就是它在这个LIS中的位置，$++cnt[L[i]]$，如果存在某一个$cnt==1$那么这个位置就是出现在了所有的LIS中，答案为$max(k-1,ansl[i]+ansr[i]+1)$，否则的话就是$max(k,ansl[i]+ansr[i]+1)$

jzoj3852,3853,3854

T1分数规划，求$\frac{ans}{node}$（$ans$为总边权，$node$为点数），二分一个答案$mid$，如果前面那个东西大于$mid$，化简一下就是$ans-node*mid>0$，转化为所有边权减去$mid$之后图上是否有正环，用spfa跑一下就好了。（然而我似乎spfa判正环一直都写错了……复杂度严重退化orz）。
T2状压dp

T3树状数组+动态开点线段树，然而我数据结构似乎做傻了……先预处理出每一个人做队长最多有几个队员，离散化之后按$r$排序，然后用树状数组维护即可。然后把询问离线，每一个询问有一个$top$表示领导力必须大于等于，那么把所有人按领导力降序排序然后用线段树维护最大值即可

jzoj5925. 【NOIP2018模拟10.25】naive 的瓶子

dp。因为瓶子只有两种可能，一是直接染成目标颜色，二是先染成权值小的颜色再染成目标颜色。那么考虑dp，设$f_i$表示将前$i$个数染成目标颜色所需的最小代价，正着跑一遍，反着跑一遍，更新答案。然后再枚举颜色继续做就行了

P4117 [Ynoi2018]五彩斑斓的世界

照着题解敲了半天……这题时空双卡……

jzoj5932. 【NOIP2018模拟10.27】情报中心

用bitset，$f[i][j]$表示从$i$点经过不超过$j$的距离能到达的点的集合，空间刚好能卡过……于是对每一个点跑一遍最短路然后前缀或一下就行了。询问时直接把所有点的答案或起来

jzoj5933. 【NOIP2018模拟10.27】百鸽笼

把序列倒过来，当成主席树的板子做就可以了。注意要记得每一次更新都要直接覆盖之前的

jzoj5893. 【NOIP2018模拟10.4】括号序列

暴力的话，枚举左端点，然后向右扩展并维护一个栈，如果新加的元素和栈顶相同弹出栈顶，否则入栈。如果某一时刻栈内元素为$0$则$++ans$。考虑优化，若$i$加入栈后和$j$加入栈后栈内的元素相等，说明$[i+1,j]$区间符合条件。于是我们一遍做过去，用map记录栈内元素的哈希值，最后计算答案即可。也可以用trie树来维护，记录一下每个节点的cnt即可，比哈希快

jzoj5895. 【NOIP2018模拟10.5】旅游

就是求欧拉回路，无向图欧拉回路只要在所有点度数都为偶数时才存在，于是在所有的奇数点之间连边。因为边权很鬼畜……每两个奇数点之间的最短路肯定是他们最小生成树上的边。于是先加上所有边的答案。然后对于每条边，判断它两侧的奇度点个数是否都是奇数个，如果是的话这条边的边权再加一次

jzoj5888. 【NOIP2018模拟9.29】GCD生成树

先把相等的连起来，然后把每一个数字看成一个点，从大到小枚举gcd，把所有有这个gcd而且不在同一连通块的连起来。因为是从大到小枚举，可以保证两个点一定只有在gcd的时候会被合并

jzoj5344. 【NOIP2017模拟9.3A组】摘果子

好像是一个叫做树上依赖背包的东西？首先每个点的选择必须先选它父亲，所以选择有强制性，即$f[u][j]=f[u][j-w[j]]+v[j]$，然后选择的话要么整条链都选，要么都不选，则$f[u][j]=max(f[u][j],f[v][j])$，然后从下往上递推即可。注意要把父亲的状态转移到儿子身上，memcpy一下就行了

jzoj4736. 【NOIP2016提高A组模拟8.25】漆黑列车载运数个谎言

看到GOSICK的题有种伤心的感觉不知道为什么。首先逆否命题和原命题的真假性是一样的，那么我们就可以把操作0看做成为朋友，操作1和2看做成为敌人，那么询问就是看这两个是不是朋友就行了

jzoj4737. 【NOIP2016提高A组模拟8.25】金色丝线将瞬间一分为二

因为是曼哈顿距离所以可以两维分别考虑。一个比较明显的暴力是我们二分答案$mid$，然后对前$mid$个排序，处理一遍看看总的距离之和是否大于$D$，时间复杂度为$O(nlog^2n)$。发现这样的话瓶颈在排序上。于是我们不用每一次都排序，可以先在最开始的时候排好序，然后记录一下排名就可以了

jzoj4738. 【NOIP2016提高A组模拟8.25】神在夏至祭降下了神谕

转移方程不难推得$f[i]=\sum f[j](|s[i]-s[j]|\leq K)$。（$s$表示$0$和$1$的个数差的前缀和）然后因为每一次都是在一个区间里的答案，所以可以用树状数组维护。不过因为有负数，所以值域要开大一点

jzoj5849. 【NOIP提高组模拟2018.8.25】d

题目要求最大化$min(x)*min(y)$，那么我们先按$x$排个序，从大到小枚举，然后把$b$全都扔进优先队列里，每次把堆顶取出来就行了

P4649 [IOI2007] training 训练路径

题解

jozj100041. 列车调度

总之就是对于每一个新加入的数，找到大于它的最小的数放在它后面，可以发现这样绝对不会比其他方法劣。想了各种奇奇怪怪的姿势都有点问题，于是没办法只能用set暴力模拟了。

jzoj3717. 火车(train)

据说正解并查集然而我不会，只会暴力的树剖。总而言之就是每一次路径覆盖，然后每一次判断下一个要到的点是否已经到过就可以了。加上几发大力剪枝可以过，就是在覆盖的时候如果本区间已经所有数都覆盖过就不用再递归下去了，以及查询的时候如果本区间所有数都被覆盖也不用再继续递归了。然而被细节卡死……首先查询的时候忘了按dfs序查，其次这题卡深搜，只要手动模拟深搜，再然后手动模拟的时候栈和队列搞混了……

P3320 [SDOI2015]寻宝游戏

不难（完全不知道怎么）看出，如果我们按dfs序把所有的被选择的点给排列起来，然后再把相邻点之间的距离加起来（包括首尾，也算相邻），就是答案了。于是我们可以用set来存储当前有宝藏的点的dfs序，以插入为例，设当前插入点为$u$，dfs序比它大的第一个点为$w$，比它小的第一个点为$v$，那么答案就要加上$dis(u,v)+dis(u,w)$，然后再减去$dis(v,w)$，减去同理。然后输出答案就可以了

bzoj3029 守卫者的挑战

概率dp真的是一塌糊涂……设$f[i][j][k]$表示当前打了$i$场，赢了$j$场，剩余背包容量为$k$（因为需要的最大容量不会超过$n$，所以这一维可以剪枝），且能装下所有地图的概率。考虑当前这一场，若是失败，则$f[i+1][j][k]+=f[i][j][k]*(1-p[i+1])$，否则$f[i+1][j+1][k+v[i+1]]+=f[i][j][k]*p[i+1]$。我们将所有的比赛中能拿到背包的放前面，这样可以保证后面取地图的时候可以直接判断空间够不够